Tensor Star Decomposition
Paper and Code
Mar 15, 2024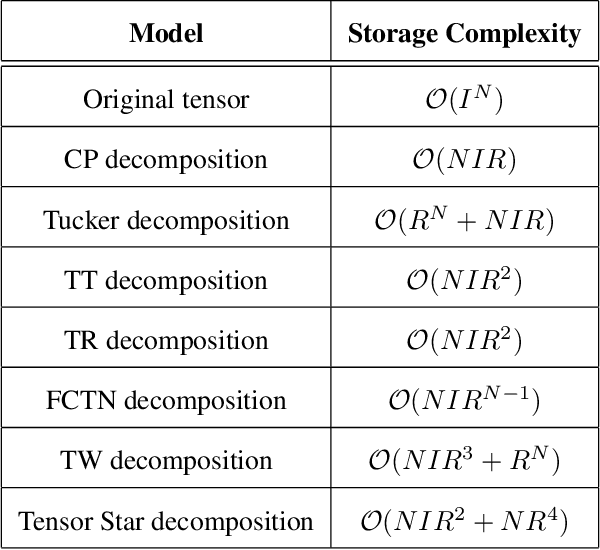
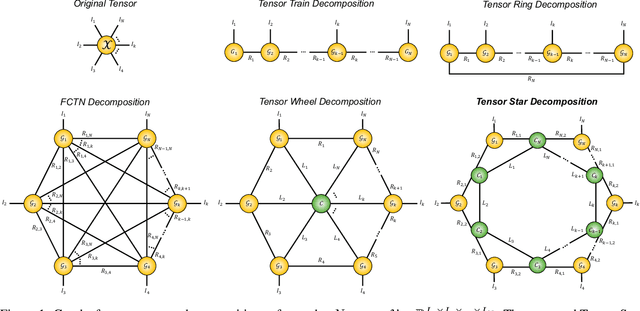
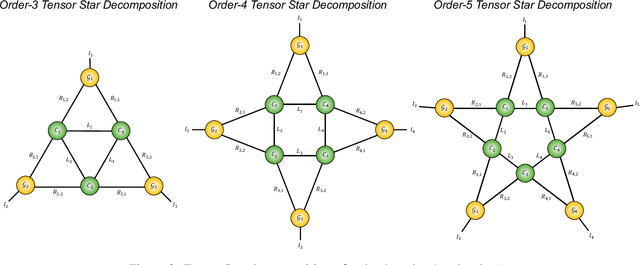
A novel tensor decomposition framework, termed Tensor Star (TS) decomposition, is proposed which represents a new type of tensor network decomposition based on tensor contractions. This is achieved by connecting the core tensors in a ring shape, whereby the core tensors act as skip connections between the factor tensors and allow for direct correlation characterisation between any two arbitrary dimensions. Uniquely, this makes it possible to decompose an order-$N$ tensor into $N$ order-$3$ factor tensors $\{\mathcal{G}_{k}\}_{k=1}^{N}$ and $N$ order-$4$ core tensors $\{\mathcal{C}_{k}\}_{k=1}^{N}$, which are arranged in a star shape. Unlike the class of Tensor Train (TT) decompositions, these factor tensors are not directly connected to one another. The so obtained core tensors also enable consecutive factor tensors to have different latent ranks. In this way, the TS decomposition alleviates the "curse of dimensionality" and controls the "curse of ranks", exhibiting a storage complexity which scales linearly with the number of dimensions and as the fourth power of the ranks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge