Provable Effects of Data Replay in Continual Learning: A Feature Learning Perspective

Continual learning (CL) aims to train models on a sequence of tasks while retaining performance on previously learned ones. A core challenge in this setting is catastrophic forgetting, where new learning interferes with past knowledge. Among various mitigation strategies, data-replay methods, where past samples are periodically revisited, are considered simple yet effective, especially when memory constraints are relaxed. However, the theoretical effectiveness of full data replay, where all past data is accessible during training, remains largely unexplored. In this paper, we present a comprehensive theoretical framework for analyzing full data-replay training in continual learning from a feature learning perspective. Adopting a multi-view data model, we identify the signal-to-noise ratio (SNR) as a critical factor affecting forgetting. Focusing on task-incremental binary classification across $M$ tasks, our analysis verifies two key conclusions: (1) forgetting can still occur under full replay when the cumulative noise from later tasks dominates the signal from earlier ones; and (2) with sufficient signal accumulation, data replay can recover earlier tasks-even if their initial learning was poor. Notably, we uncover a novel insight into task ordering: prioritizing higher-signal tasks not only facilitates learning of lower-signal tasks but also helps prevent catastrophic forgetting. We validate our theoretical findings through synthetic and real-world experiments that visualize the interplay between signal learning and noise memorization across varying SNRs and task correlation regimes.

Finding Differentially Private Second Order Stationary Points in Stochastic Minimax Optimization

We provide the first study of the problem of finding differentially private (DP) second-order stationary points (SOSP) in stochastic (non-convex) minimax optimization. Existing literature either focuses only on first-order stationary points for minimax problems or on SOSP for classical stochastic minimization problems. This work provides, for the first time, a unified and detailed treatment of both empirical and population risks. Specifically, we propose a purely first-order method that combines a nested gradient descent--ascent scheme with SPIDER-style variance reduction and Gaussian perturbations to ensure privacy. A key technical device is a block-wise ($q$-period) analysis that controls the accumulation of stochastic variance and privacy noise without summing over the full iteration horizon, yielding a unified treatment of both empirical-risk and population formulations. Under standard smoothness, Hessian-Lipschitzness, and strong concavity assumptions, we establish high-probability guarantees for reaching an $(α,\sqrt{ρ_Φα})$-approximate second-order stationary point with $α= \mathcal{O}( (\frac{\sqrt{d}}{n\varepsilon})^{2/3})$ for empirical risk objectives and $\mathcal{O}(\frac{1}{n^{1/3}} + (\frac{\sqrt{d}}{n\varepsilon})^{1/2})$ for population objectives, matching the best known rates for private first-order stationarity.

In-Run Data Shapley for Adam Optimizer

Reliable data attribution is essential for mitigating bias and reducing computational waste in modern machine learning, with the Shapley value serving as the theoretical gold standard. While recent "In-Run" methods bypass the prohibitive cost of retraining by estimating contributions dynamically, they heavily rely on the linear structure of Stochastic Gradient Descent (SGD) and fail to capture the complex dynamics of adaptive optimizers like Adam. In this work, we demonstrate that data attribution is inherently optimizer-dependent: we show that SGD-based proxies diverge significantly from true contributions under Adam (Pearson $R \approx 0.11$), rendering them ineffective for modern training pipelines. To bridge this gap, we propose Adam-Aware In-Run Data Shapley. We derive a closed-form approximation that restores additivity by redefining utility under a fixed-state assumption and enable scalable computation via a novel Linearized Ghost Approximation. This technique linearizes the variance-dependent scaling term, allowing us to compute pairwise gradient dot-products without materializing per-sample gradients. Extensive experiments show that our method achieves near-perfect fidelity to ground-truth marginal contributions ($R > 0.99$) while retaining $\sim$95\% of standard training throughput. Furthermore, our Adam-aware attribution significantly outperforms SGD-based baselines in data attribution downstream tasks.

Rethinking Coupled Tensor Analysis for Hyperspectral Super-Resolution: Recoverable Modeling Under Endmember Variability

This work revisits the hyperspectral super-resolution (HSR) problem, i.e., fusing a pair of spatially co-registered hyperspectral (HSI) and multispectral (MSI) images to recover a super-resolution image (SRI) that enhances the spatial resolution of the HSI. Coupled tensor decomposition (CTD)-based methods have gained traction in this domain, offering recoverability guarantees under various assumptions. Existing models such as canonical polyadic decomposition (CPD) and Tucker decomposition provide strong expressive power but lack physical interpretability. The block-term decomposition model with rank-$(L_r, L_r, 1)$ terms (the LL1 model) yields interpretable factors under the linear mixture model (LMM) of spectral images, but LMM assumptions are often violated in practice -- primarily due to nonlinear effects such as endmember variability (EV). To address this, we propose modeling spectral images using a more flexible block-term tensor decomposition with rank-$(L_r, M_r, N_r)$ terms (the LMN model). This modeling choice retains interpretability, subsumes CPD, Tucker, and LL1 as special cases, and robustly accounts for non-ideal effects such as EV, offering a balanced tradeoff between expressiveness and interpretability for HSR. Importantly, under the LMN model for HSI and MSI, recoverability of the SRI can still be established under proper conditions -- providing strong theoretical support. Extensive experiments on synthetic and real datasets further validate the effectiveness and robustness of the proposed method compared with existing CTD-based approaches.

Beyond Ordinary Lipschitz Constraints: Differentially Private Stochastic Optimization with Tsybakov Noise Condition

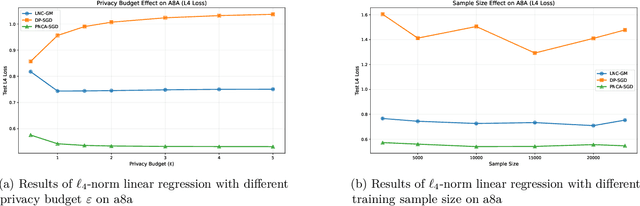
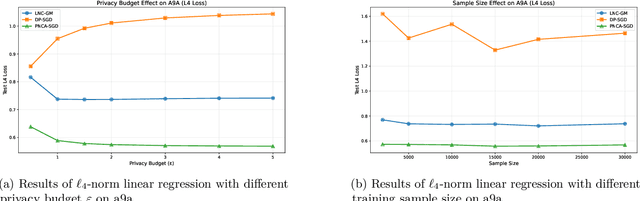
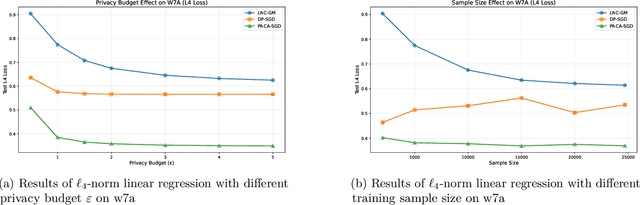
We study Stochastic Convex Optimization in the Differential Privacy model (DP-SCO). Unlike previous studies, here we assume the population risk function satisfies the Tsybakov Noise Condition (TNC) with some parameter $\theta>1$, where the Lipschitz constant of the loss could be extremely large or even unbounded, but the $\ell_2$-norm gradient of the loss has bounded $k$-th moment with $k\geq 2$. For the Lipschitz case with $\theta\geq 2$, we first propose an $(\varepsilon, \delta)$-DP algorithm whose utility bound is $\Tilde{O}\left(\left(\tilde{r}_{2k}(\frac{1}{\sqrt{n}}+(\frac{\sqrt{d}}{n\varepsilon}))^\frac{k-1}{k}\right)^\frac{\theta}{\theta-1}\right)$ in high probability, where $n$ is the sample size, $d$ is the model dimension, and $\tilde{r}_{2k}$ is a term that only depends on the $2k$-th moment of the gradient. It is notable that such an upper bound is independent of the Lipschitz constant. We then extend to the case where $\theta\geq \bar{\theta}> 1$ for some known constant $\bar{\theta}$. Moreover, when the privacy budget $\varepsilon$ is small enough, we show an upper bound of $\tilde{O}\left(\left(\tilde{r}_{k}(\frac{1}{\sqrt{n}}+(\frac{\sqrt{d}}{n\varepsilon}))^\frac{k-1}{k}\right)^\frac{\theta}{\theta-1}\right)$ even if the loss function is not Lipschitz. For the lower bound, we show that for any $\theta\geq 2$, the private minimax rate for $\rho$-zero Concentrated Differential Privacy is lower bounded by $\Omega\left(\left(\tilde{r}_{k}(\frac{1}{\sqrt{n}}+(\frac{\sqrt{d}}{n\sqrt{\rho}}))^\frac{k-1}{k}\right)^\frac{\theta}{\theta-1}\right)$.

Differentially Private Sparse Linear Regression with Heavy-tailed Responses

As a fundamental problem in machine learning and differential privacy (DP), DP linear regression has been extensively studied. However, most existing methods focus primarily on either regular data distributions or low-dimensional cases with irregular data. To address these limitations, this paper provides a comprehensive study of DP sparse linear regression with heavy-tailed responses in high-dimensional settings. In the first part, we introduce the DP-IHT-H method, which leverages the Huber loss and private iterative hard thresholding to achieve an estimation error bound of \( \tilde{O}\biggl( s^{* \frac{1 }{2}} \cdot \biggl(\frac{\log d}{n}\biggr)^{\frac{\zeta}{1 + \zeta}} + s^{* \frac{1 + 2\zeta}{2 + 2\zeta}} \cdot \biggl(\frac{\log^2 d}{n \varepsilon}\biggr)^{\frac{\zeta}{1 + \zeta}} \biggr) \) under the $(\varepsilon, \delta)$-DP model, where $n$ is the sample size, $d$ is the dimensionality, $s^*$ is the sparsity of the parameter, and $\zeta \in (0, 1]$ characterizes the tail heaviness of the data. In the second part, we propose DP-IHT-L, which further improves the error bound under additional assumptions on the response and achieves \( \tilde{O}\Bigl(\frac{(s^*)^{3/2} \log d}{n \varepsilon}\Bigr). \) Compared to the first result, this bound is independent of the tail parameter $\zeta$. Finally, through experiments on synthetic and real-world datasets, we demonstrate that our methods outperform standard DP algorithms designed for ``regular'' data.

Nearly Optimal Differentially Private ReLU Regression

In this paper, we investigate one of the most fundamental nonconvex learning problems, ReLU regression, in the Differential Privacy (DP) model. Previous studies on private ReLU regression heavily rely on stringent assumptions, such as constant bounded norms for feature vectors and labels. We relax these assumptions to a more standard setting, where data can be i.i.d. sampled from $O(1)$-sub-Gaussian distributions. We first show that when $\varepsilon = \tilde{O}(\sqrt{\frac{1}{N}})$ and there is some public data, it is possible to achieve an upper bound of $\Tilde{O}(\frac{d^2}{N^2 \varepsilon^2})$ for the excess population risk in $(\epsilon, \delta)$-DP, where $d$ is the dimension and $N$ is the number of data samples. Moreover, we relax the requirement of $\epsilon$ and public data by proposing and analyzing a one-pass mini-batch Generalized Linear Model Perceptron algorithm (DP-MBGLMtron). Additionally, using the tracing attack argument technique, we demonstrate that the minimax rate of the estimation error for $(\varepsilon, \delta)$-DP algorithms is lower bounded by $\Omega(\frac{d^2}{N^2 \varepsilon^2})$. This shows that DP-MBGLMtron achieves the optimal utility bound up to logarithmic factors. Experiments further support our theoretical results.

Towards User-level Private Reinforcement Learning with Human Feedback

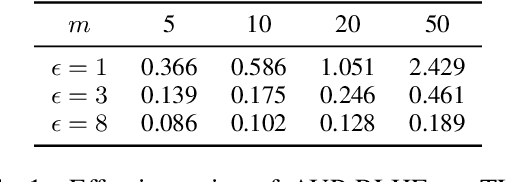
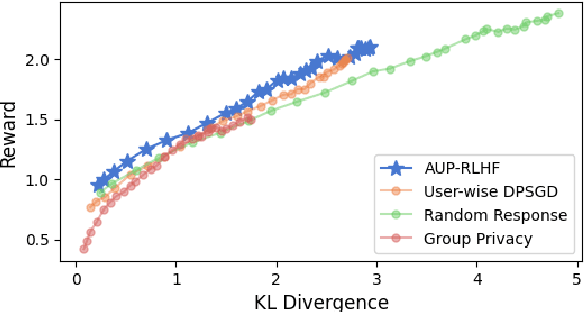
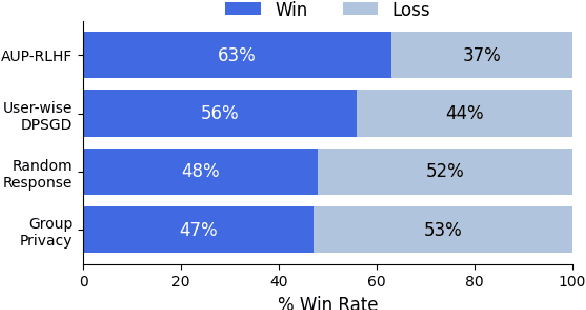
Reinforcement Learning with Human Feedback (RLHF) has emerged as an influential technique, enabling the alignment of large language models (LLMs) with human preferences. Despite the promising potential of RLHF, how to protect user preference privacy has become a crucial issue. Most previous work has focused on using differential privacy (DP) to protect the privacy of individual data. However, they have concentrated primarily on item-level privacy protection and have unsatisfactory performance for user-level privacy, which is more common in RLHF. This study proposes a novel framework, AUP-RLHF, which integrates user-level label DP into RLHF. We first show that the classical random response algorithm, which achieves an acceptable performance in item-level privacy, leads to suboptimal utility when in the user-level settings. We then establish a lower bound for the user-level label DP-RLHF and develop the AUP-RLHF algorithm, which guarantees $(\varepsilon, \delta)$ user-level privacy and achieves an improved estimation error. Experimental results show that AUP-RLHF outperforms existing baseline methods in sentiment generation and summarization tasks, achieving a better privacy-utility trade-off.

Evaluating Data Influence in Meta Learning

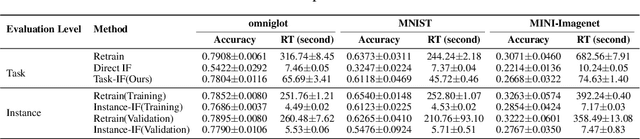
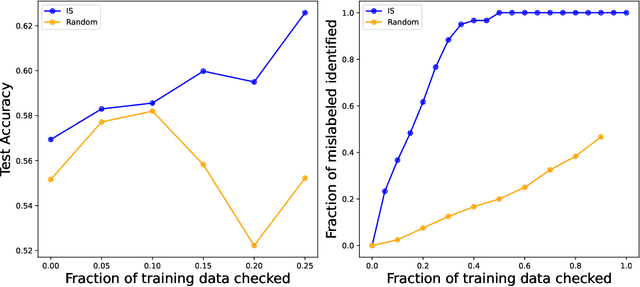
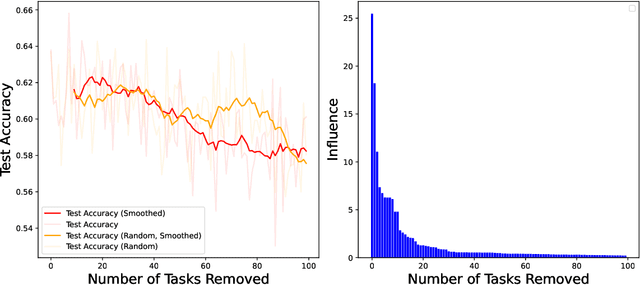
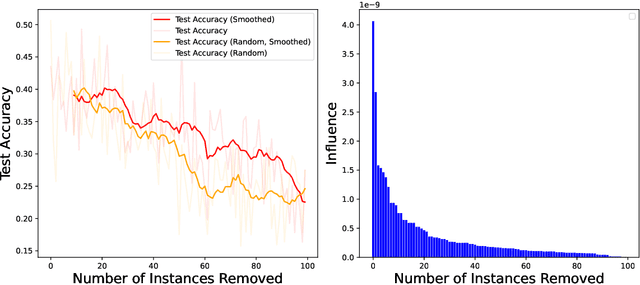
As one of the most fundamental models, meta learning aims to effectively address few-shot learning challenges. However, it still faces significant issues related to the training data, such as training inefficiencies due to numerous low-contribution tasks in large datasets and substantial noise from incorrect labels. Thus, training data attribution methods are needed for meta learning. However, the dual-layer structure of mata learning complicates the modeling of training data contributions because of the interdependent influence between meta-parameters and task-specific parameters, making existing data influence evaluation tools inapplicable or inaccurate. To address these challenges, based on the influence function, we propose a general data attribution evaluation framework for meta-learning within the bilevel optimization framework. Our approach introduces task influence functions (task-IF) and instance influence functions (instance-IF) to accurately assess the impact of specific tasks and individual data points in closed forms. This framework comprehensively models data contributions across both the inner and outer training processes, capturing the direct effects of data points on meta-parameters as well as their indirect influence through task-specific parameters. We also provide several strategies to enhance computational efficiency and scalability. Experimental results demonstrate the framework's effectiveness in training data evaluation via several downstream tasks.

TTVD: Towards a Geometric Framework for Test-Time Adaptation Based on Voronoi Diagram

Deep learning models often struggle with generalization when deploying on real-world data, due to the common distributional shift to the training data. Test-time adaptation (TTA) is an emerging scheme used at inference time to address this issue. In TTA, models are adapted online at the same time when making predictions to test data. Neighbor-based approaches have gained attention recently, where prototype embeddings provide location information to alleviate the feature shift between training and testing data. However, due to their inherit limitation of simplicity, they often struggle to learn useful patterns and encounter performance degradation. To confront this challenge, we study the TTA problem from a geometric point of view. We first reveal that the underlying structure of neighbor-based methods aligns with the Voronoi Diagram, a classical computational geometry model for space partitioning. Building on this observation, we propose the Test-Time adjustment by Voronoi Diagram guidance (TTVD), a novel framework that leverages the benefits of this geometric property. Specifically, we explore two key structures: 1) Cluster-induced Voronoi Diagram (CIVD): This integrates the joint contribution of self-supervision and entropy-based methods to provide richer information. 2) Power Diagram (PD): A generalized version of the Voronoi Diagram that refines partitions by assigning weights to each Voronoi cell. Our experiments under rigid, peer-reviewed settings on CIFAR-10-C, CIFAR-100-C, ImageNet-C, and ImageNet-R shows that TTVD achieves remarkable improvements compared to state-of-the-art methods. Moreover, extensive experimental results also explore the effects of batch size and class imbalance, which are two scenarios commonly encountered in real-world applications. These analyses further validate the robustness and adaptability of our proposed framework.