Nearly Optimal Differentially Private ReLU Regression

In this paper, we investigate one of the most fundamental nonconvex learning problems, ReLU regression, in the Differential Privacy (DP) model. Previous studies on private ReLU regression heavily rely on stringent assumptions, such as constant bounded norms for feature vectors and labels. We relax these assumptions to a more standard setting, where data can be i.i.d. sampled from $O(1)$-sub-Gaussian distributions. We first show that when $\varepsilon = \tilde{O}(\sqrt{\frac{1}{N}})$ and there is some public data, it is possible to achieve an upper bound of $\Tilde{O}(\frac{d^2}{N^2 \varepsilon^2})$ for the excess population risk in $(\epsilon, \delta)$-DP, where $d$ is the dimension and $N$ is the number of data samples. Moreover, we relax the requirement of $\epsilon$ and public data by proposing and analyzing a one-pass mini-batch Generalized Linear Model Perceptron algorithm (DP-MBGLMtron). Additionally, using the tracing attack argument technique, we demonstrate that the minimax rate of the estimation error for $(\varepsilon, \delta)$-DP algorithms is lower bounded by $\Omega(\frac{d^2}{N^2 \varepsilon^2})$. This shows that DP-MBGLMtron achieves the optimal utility bound up to logarithmic factors. Experiments further support our theoretical results.

Towards User-level Private Reinforcement Learning with Human Feedback

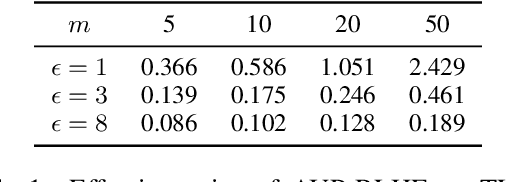
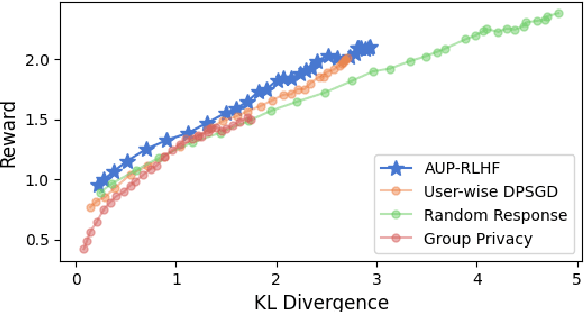
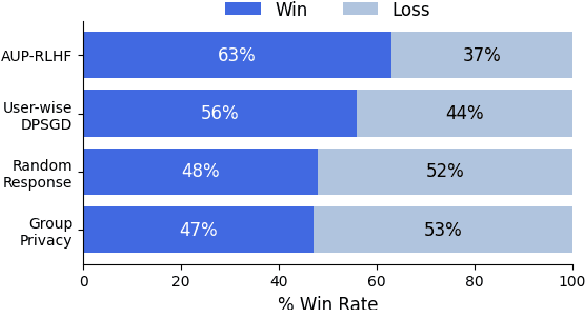
Reinforcement Learning with Human Feedback (RLHF) has emerged as an influential technique, enabling the alignment of large language models (LLMs) with human preferences. Despite the promising potential of RLHF, how to protect user preference privacy has become a crucial issue. Most previous work has focused on using differential privacy (DP) to protect the privacy of individual data. However, they have concentrated primarily on item-level privacy protection and have unsatisfactory performance for user-level privacy, which is more common in RLHF. This study proposes a novel framework, AUP-RLHF, which integrates user-level label DP into RLHF. We first show that the classical random response algorithm, which achieves an acceptable performance in item-level privacy, leads to suboptimal utility when in the user-level settings. We then establish a lower bound for the user-level label DP-RLHF and develop the AUP-RLHF algorithm, which guarantees $(\varepsilon, \delta)$ user-level privacy and achieves an improved estimation error. Experimental results show that AUP-RLHF outperforms existing baseline methods in sentiment generation and summarization tasks, achieving a better privacy-utility trade-off.

TTVD: Towards a Geometric Framework for Test-Time Adaptation Based on Voronoi Diagram

Deep learning models often struggle with generalization when deploying on real-world data, due to the common distributional shift to the training data. Test-time adaptation (TTA) is an emerging scheme used at inference time to address this issue. In TTA, models are adapted online at the same time when making predictions to test data. Neighbor-based approaches have gained attention recently, where prototype embeddings provide location information to alleviate the feature shift between training and testing data. However, due to their inherit limitation of simplicity, they often struggle to learn useful patterns and encounter performance degradation. To confront this challenge, we study the TTA problem from a geometric point of view. We first reveal that the underlying structure of neighbor-based methods aligns with the Voronoi Diagram, a classical computational geometry model for space partitioning. Building on this observation, we propose the Test-Time adjustment by Voronoi Diagram guidance (TTVD), a novel framework that leverages the benefits of this geometric property. Specifically, we explore two key structures: 1) Cluster-induced Voronoi Diagram (CIVD): This integrates the joint contribution of self-supervision and entropy-based methods to provide richer information. 2) Power Diagram (PD): A generalized version of the Voronoi Diagram that refines partitions by assigning weights to each Voronoi cell. Our experiments under rigid, peer-reviewed settings on CIFAR-10-C, CIFAR-100-C, ImageNet-C, and ImageNet-R shows that TTVD achieves remarkable improvements compared to state-of-the-art methods. Moreover, extensive experimental results also explore the effects of batch size and class imbalance, which are two scenarios commonly encountered in real-world applications. These analyses further validate the robustness and adaptability of our proposed framework.

On Stability and Generalization of Bilevel Optimization Problem

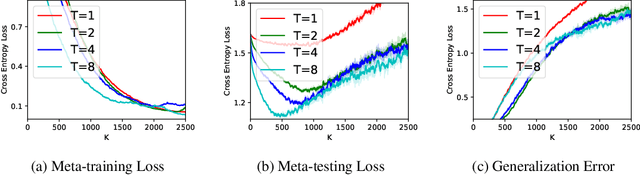
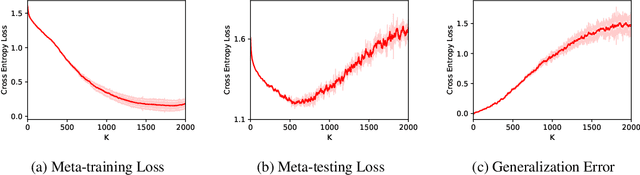
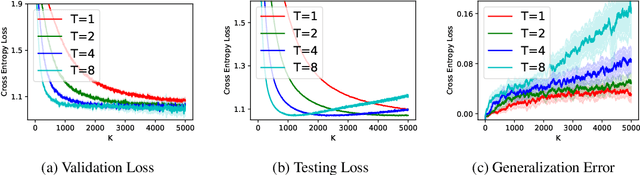
(Stochastic) bilevel optimization is a frequently encountered problem in machine learning with a wide range of applications such as meta-learning, hyper-parameter optimization, and reinforcement learning. Most of the existing studies on this problem only focused on analyzing the convergence or improving the convergence rate, while little effort has been devoted to understanding its generalization behaviors. In this paper, we conduct a thorough analysis on the generalization of first-order (gradient-based) methods for the bilevel optimization problem. We first establish a fundamental connection between algorithmic stability and generalization error in different forms and give a high probability generalization bound which improves the previous best one from $\bigO(\sqrt{n})$ to $\bigO(\log n)$, where $n$ is the sample size. We then provide the first stability bounds for the general case where both inner and outer level parameters are subject to continuous update, while existing work allows only the outer level parameter to be updated. Our analysis can be applied in various standard settings such as strongly-convex-strongly-convex (SC-SC), convex-convex (C-C), and nonconvex-nonconvex (NC-NC). Our analysis for the NC-NC setting can also be extended to a particular nonconvex-strongly-convex (NC-SC) setting that is commonly encountered in practice. Finally, we corroborate our theoretical analysis and demonstrate how iterations can affect the generalization error by experiments on meta-learning and hyper-parameter optimization.

Benchmarking features from different radiomics toolkits / toolboxes using Image Biomarkers Standardization Initiative

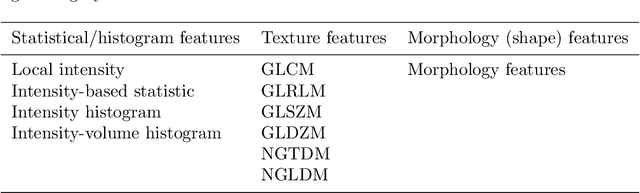
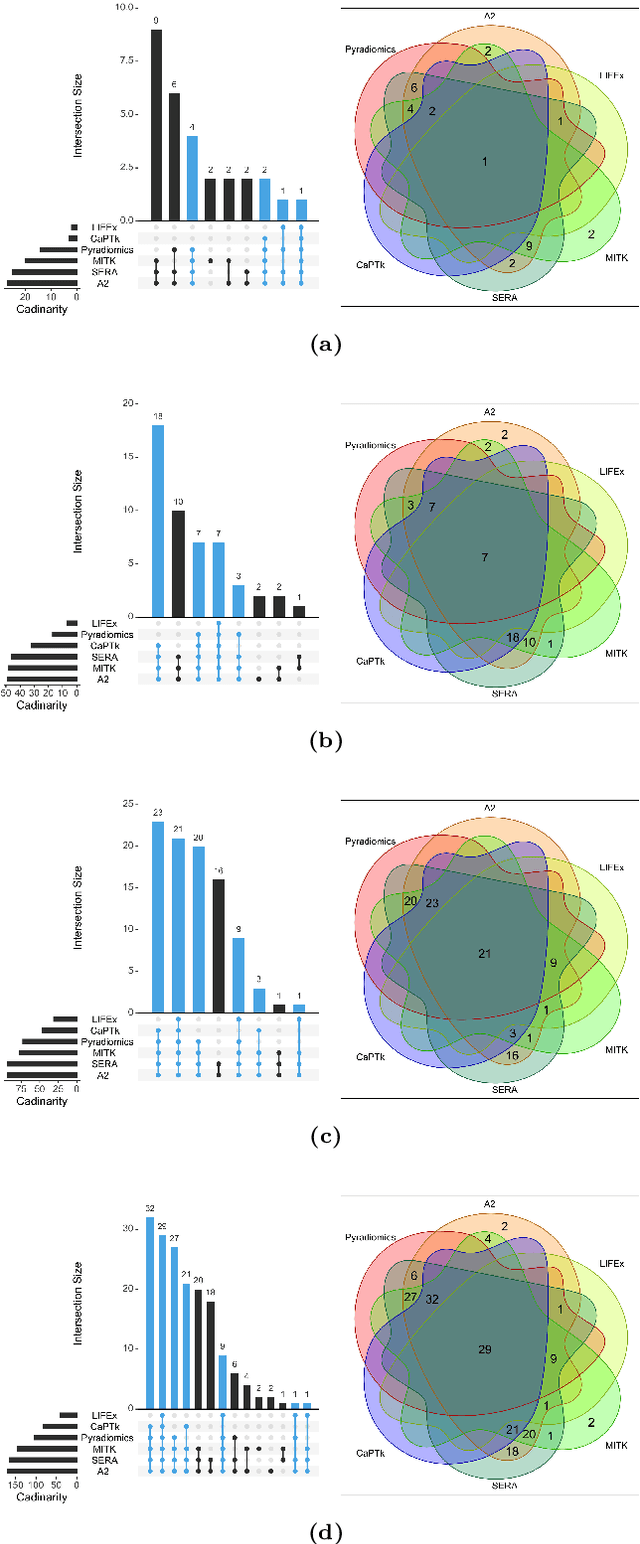
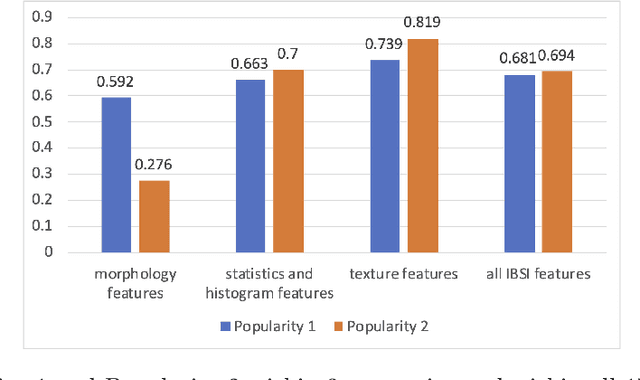
There is no consensus regarding the radiomic feature terminology, the underlying mathematics, or their implementation. This creates a scenario where features extracted using different toolboxes could not be used to build or validate the same model leading to a non-generalization of radiomic results. In this study, the image biomarker standardization initiative (IBSI) established phantom and benchmark values were used to compare the variation of the radiomic features while using 6 publicly available software programs and 1 in-house radiomics pipeline. All IBSI-standardized features (11 classes, 173 in total) were extracted. The relative differences between the extracted feature values from the different software and the IBSI benchmark values were calculated to measure the inter-software agreement. To better understand the variations, features are further grouped into 3 categories according to their properties: 1) morphology, 2) statistic/histogram and 3)texture features. While a good agreement was observed for a majority of radiomics features across the various programs, relatively poor agreement was observed for morphology features. Significant differences were also found in programs that use different gray level discretization approaches. Since these programs do not include all IBSI features, the level of quantitative assessment for each category was analyzed using Venn and the UpSet diagrams and also quantified using two ad hoc metrics. Morphology features earns lowest scores for both metrics, indicating that morphological features are not consistently evaluated among software programs. We conclude that radiomic features calculated using different software programs may not be identical and reliable. Further studies are needed to standardize the workflow of radiomic feature extraction.