TTVD: Towards a Geometric Framework for Test-Time Adaptation Based on Voronoi Diagram

Deep learning models often struggle with generalization when deploying on real-world data, due to the common distributional shift to the training data. Test-time adaptation (TTA) is an emerging scheme used at inference time to address this issue. In TTA, models are adapted online at the same time when making predictions to test data. Neighbor-based approaches have gained attention recently, where prototype embeddings provide location information to alleviate the feature shift between training and testing data. However, due to their inherit limitation of simplicity, they often struggle to learn useful patterns and encounter performance degradation. To confront this challenge, we study the TTA problem from a geometric point of view. We first reveal that the underlying structure of neighbor-based methods aligns with the Voronoi Diagram, a classical computational geometry model for space partitioning. Building on this observation, we propose the Test-Time adjustment by Voronoi Diagram guidance (TTVD), a novel framework that leverages the benefits of this geometric property. Specifically, we explore two key structures: 1) Cluster-induced Voronoi Diagram (CIVD): This integrates the joint contribution of self-supervision and entropy-based methods to provide richer information. 2) Power Diagram (PD): A generalized version of the Voronoi Diagram that refines partitions by assigning weights to each Voronoi cell. Our experiments under rigid, peer-reviewed settings on CIFAR-10-C, CIFAR-100-C, ImageNet-C, and ImageNet-R shows that TTVD achieves remarkable improvements compared to state-of-the-art methods. Moreover, extensive experimental results also explore the effects of batch size and class imbalance, which are two scenarios commonly encountered in real-world applications. These analyses further validate the robustness and adaptability of our proposed framework.

Multiset Transformer: Advancing Representation Learning in Persistence Diagrams

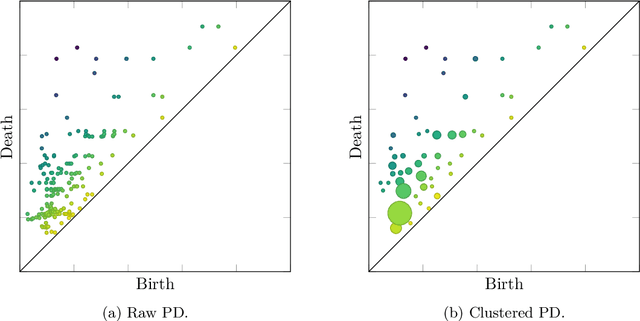
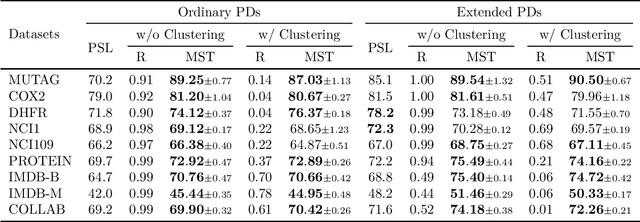
To improve persistence diagram representation learning, we propose Multiset Transformer. This is the first neural network that utilizes attention mechanisms specifically designed for multisets as inputs and offers rigorous theoretical guarantees of permutation invariance. The architecture integrates multiset-enhanced attentions with a pool-decomposition scheme, allowing multiplicities to be preserved across equivariant layers. This capability enables full leverage of multiplicities while significantly reducing both computational and spatial complexity compared to the Set Transformer. Additionally, our method can greatly benefit from clustering as a preprocessing step to further minimize complexity, an advantage not possessed by the Set Transformer. Experimental results demonstrate that the Multiset Transformer outperforms existing neural network methods in the realm of persistence diagram representation learning.

Progressive Voronoi Diagram Subdivision: Towards A Holistic Geometric Framework for Exemplar-free Class-Incremental Learning

Exemplar-free Class-incremental Learning (CIL) is a challenging problem because rehearsing data from previous phases is strictly prohibited, causing catastrophic forgetting of Deep Neural Networks (DNNs). In this paper, we present iVoro, a holistic framework for CIL, derived from computational geometry. We found Voronoi Diagram (VD), a classical model for space subdivision, is especially powerful for solving the CIL problem, because VD itself can be constructed favorably in an incremental manner -- the newly added sites (classes) will only affect the proximate classes, making the non-contiguous classes hardly forgettable. Further, in order to find a better set of centers for VD construction, we colligate DNN with VD using Power Diagram and show that the VD structure can be optimized by integrating local DNN models using a divide-and-conquer algorithm. Moreover, our VD construction is not restricted to the deep feature space, but is also applicable to multiple intermediate feature spaces, promoting VD to be multi-centered VD (CIVD) that efficiently captures multi-grained features from DNN. Importantly, iVoro is also capable of handling uncertainty-aware test-time Voronoi cell assignment and has exhibited high correlations between geometric uncertainty and predictive accuracy (up to ~0.9). Putting everything together, iVoro achieves up to 25.26%, 37.09%, and 33.21% improvements on CIFAR-100, TinyImageNet, and ImageNet-Subset, respectively, compared to the state-of-the-art non-exemplar CIL approaches. In conclusion, iVoro enables highly accurate, privacy-preserving, and geometrically interpretable CIL that is particularly useful when cross-phase data sharing is forbidden, e.g. in medical applications. Our code is available at https://machunwei.github.io/ivoro.

Few-shot Learning as Cluster-induced Voronoi Diagrams: A Geometric Approach

Few-shot learning (FSL) is the process of rapid generalization from abundant base samples to inadequate novel samples. Despite extensive research in recent years, FSL is still not yet able to generate satisfactory solutions for a wide range of real-world applications. To confront this challenge, we study the FSL problem from a geometric point of view in this paper. One observation is that the widely embraced ProtoNet model is essentially a Voronoi Diagram (VD) in the feature space. We retrofit it by making use of a recent advance in computational geometry called Cluster-induced Voronoi Diagram (CIVD). Starting from the simplest nearest neighbor model, CIVD gradually incorporates cluster-to-point and then cluster-to-cluster relationships for space subdivision, which is used to improve the accuracy and robustness at multiple stages of FSL. Specifically, we use CIVD (1) to integrate parametric and nonparametric few-shot classifiers; (2) to combine feature representation and surrogate representation; (3) and to leverage feature-level, transformation-level, and geometry-level heterogeneities for a better ensemble. Our CIVD-based workflow enables us to achieve new state-of-the-art results on mini-ImageNet, CUB, and tiered-ImagenNet datasets, with ${\sim}2\%{-}5\%$ improvements upon the next best. To summarize, CIVD provides a mathematically elegant and geometrically interpretable framework that compensates for extreme data insufficiency, prevents overfitting, and allows for fast geometric ensemble for thousands of individual VD. These together make FSL stronger.

Improving Uncertainty Calibration of Deep Neural Networks via Truth Discovery and Geometric Optimization

Deep Neural Networks (DNNs), despite their tremendous success in recent years, could still cast doubts on their predictions due to the intrinsic uncertainty associated with their learning process. Ensemble techniques and post-hoc calibrations are two types of approaches that have individually shown promise in improving the uncertainty calibration of DNNs. However, the synergistic effect of the two types of methods has not been well explored. In this paper, we propose a truth discovery framework to integrate ensemble-based and post-hoc calibration methods. Using the geometric variance of the ensemble candidates as a good indicator for sample uncertainty, we design an accuracy-preserving truth estimator with provably no accuracy drop. Furthermore, we show that post-hoc calibration can also be enhanced by truth discovery-regularized optimization. On large-scale datasets including CIFAR and ImageNet, our method shows consistent improvement against state-of-the-art calibration approaches on both histogram-based and kernel density-based evaluation metrics. Our codes are available at https://github.com/horsepurve/truly-uncertain.