Multiset Transformer: Advancing Representation Learning in Persistence Diagrams

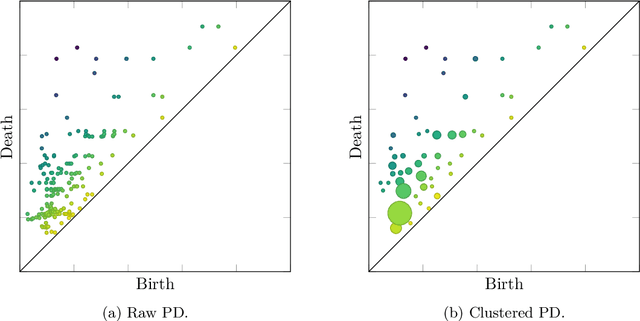
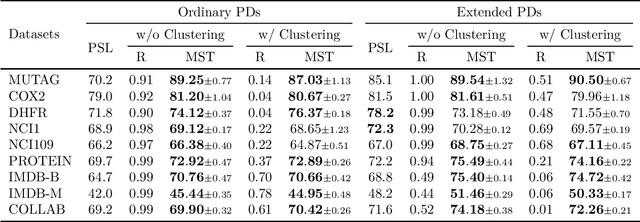
To improve persistence diagram representation learning, we propose Multiset Transformer. This is the first neural network that utilizes attention mechanisms specifically designed for multisets as inputs and offers rigorous theoretical guarantees of permutation invariance. The architecture integrates multiset-enhanced attentions with a pool-decomposition scheme, allowing multiplicities to be preserved across equivariant layers. This capability enables full leverage of multiplicities while significantly reducing both computational and spatial complexity compared to the Set Transformer. Additionally, our method can greatly benefit from clustering as a preprocessing step to further minimize complexity, an advantage not possessed by the Set Transformer. Experimental results demonstrate that the Multiset Transformer outperforms existing neural network methods in the realm of persistence diagram representation learning.

Tensor Decompositions for Hyperspectral Data Processing in Remote Sensing: A Comprehensive Review

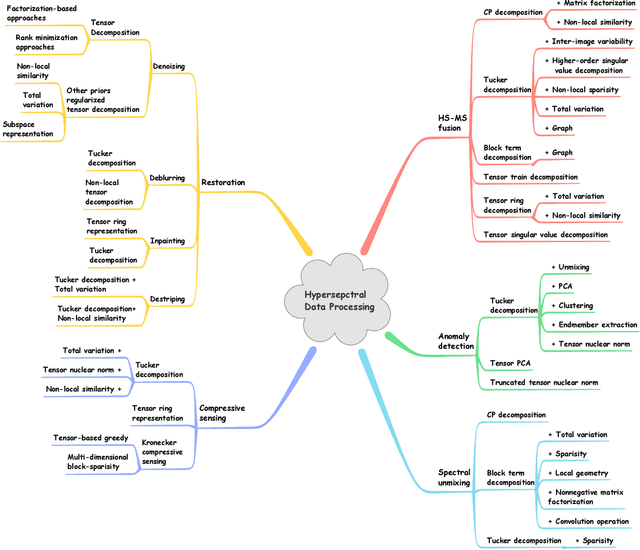
Owing to the rapid development of sensor technology, hyperspectral (HS) remote sensing (RS) imaging has provided a significant amount of spatial and spectral information for the observation and analysis of the Earth's surface at a distance of data acquisition devices, such as aircraft, spacecraft, and satellite. The recent advancement and even revolution of the HS RS technique offer opportunities to realize the full potential of various applications, while confronting new challenges for efficiently processing and analyzing the enormous HS acquisition data. Due to the maintenance of the 3-D HS inherent structure, tensor decomposition has aroused widespread concern and research in HS data processing tasks over the past decades. In this article, we aim at presenting a comprehensive overview of tensor decomposition, specifically contextualizing the five broad topics in HS data processing, and they are HS restoration, compressed sensing, anomaly detection, super-resolution, and spectral unmixing. For each topic, we elaborate on the remarkable achievements of tensor decomposition models for HS RS with a pivotal description of the existing methodologies and a representative exhibition on the experimental results. As a result, the remaining challenges of the follow-up research directions are outlined and discussed from the perspective of the real HS RS practices and tensor decomposition merged with advanced priors and even with deep neural networks. This article summarizes different tensor decomposition-based HS data processing methods and categorizes them into different classes from simple adoptions to complex combinations with other priors for the algorithm beginners. We also expect this survey can provide new investigations and development trends for the experienced researchers who understand tensor decomposition and HS RS to some extent.