Why Fine-Tuning Struggles with Forgetting in Machine Unlearning? Theoretical Insights and a Remedial Approach
Paper and Code
Oct 04, 2024


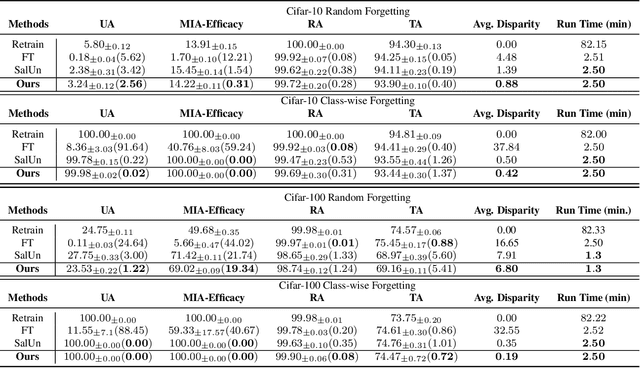
Machine Unlearning has emerged as a significant area of research, focusing on 'removing' specific subsets of data from a trained model. Fine-tuning (FT) methods have become one of the fundamental approaches for approximating unlearning, as they effectively retain model performance. However, it is consistently observed that naive FT methods struggle to forget the targeted data. In this paper, we present the first theoretical analysis of FT methods for machine unlearning within a linear regression framework, providing a deeper exploration of this phenomenon. We investigate two scenarios with distinct features and overlapping features. Our findings reveal that FT models can achieve zero remaining loss yet fail to forget the forgetting data, unlike golden models (trained from scratch without the forgetting data). This analysis reveals that naive FT methods struggle with forgetting because the pretrained model retains information about the forgetting data, and the fine-tuning process has no impact on this retained information. To address this issue, we first propose a theoretical approach to mitigate the retention of forgetting data in the pretrained model. Our analysis shows that removing the forgetting data's influence allows FT models to match the performance of the golden model. Building on this insight, we introduce a discriminative regularization term to practically reduce the unlearning loss gap between the fine-tuned model and the golden model. Our experiments on both synthetic and real-world datasets validate these theoretical insights and demonstrate the effectiveness of the proposed regularization method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge