Joint Tensor and Inter-View Low-Rank Recovery for Incomplete Multiview Clustering

Incomplete multiview clustering (IMVC) has gained significant attention for its effectiveness in handling missing sample challenges across various views in real-world multiview clustering applications. Most IMVC approaches tackle this problem by either learning consensus representations from available views or reconstructing missing samples using the underlying manifold structure. However, the reconstruction of learned similarity graph tensor in prior studies only exploits the low-tubal-rank information, neglecting the exploration of inter-view correlations. This paper propose a novel joint tensor and inter-view low-rank Recovery (JTIV-LRR), framing IMVC as a joint optimization problem that integrates incomplete similarity graph learning and tensor representation recovery. By leveraging both intra-view and inter-view low rank information, the method achieves robust estimation of the complete similarity graph tensor through sparse noise removal and low-tubal-rank constraints along different modes. Extensive experiments on both synthetic and real-world datasets demonstrate the superiority of the proposed approach, achieving significant improvements in clustering accuracy and robustness compared to state-of-the-art methods.

Determined Blind Source Separation with Sinkhorn Divergence-based Optimal Allocation of the Source Power

Blind source separation (BSS) refers to the process of recovering multiple source signals from observations recorded by an array of sensors. Common approaches to BSS, including independent vector analysis (IVA), and independent low-rank matrix analysis (ILRMA), typically rely on second-order models to capture the statistical independence of source signals for separation. However, these methods generally do not account for the implicit structural information across frequency bands, which may lead to model mismatches between the assumed source distributions and the distributions of the separated source signals estimated from the observed mixtures. To tackle these limitations, this paper shows that conventional approaches such as IVA and ILRMA can easily be leveraged by the Sinkhorn divergence, incorporating an optimal transport (OT) framework to adaptively correct source variance estimates. This allows for the recovery of the source distribution while modeling the inter-band signal dependence and reallocating source power across bands. As a result, enhanced versions of these algorithms are developed, integrating a Sinkhorn iterative scheme into their standard implementations. Extensive simulations demonstrate that the proposed methods consistently enhance BSS performance.

On-the-fly spectral unmixing based on Kalman filtering

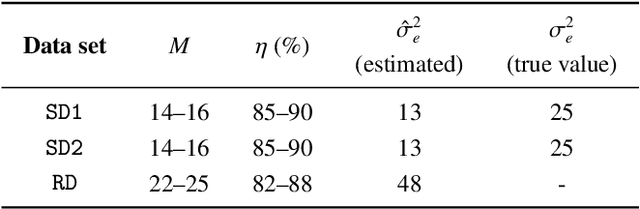
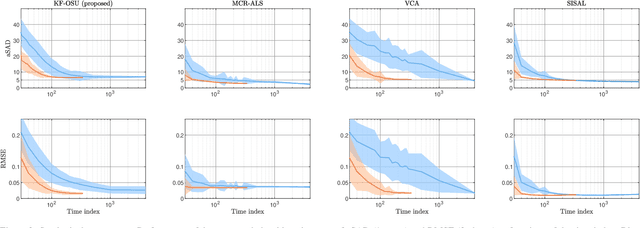
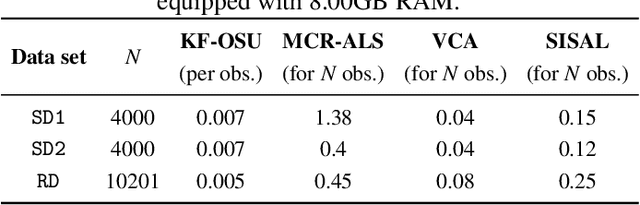
This work introduces an on-the-fly (i.e., online) linear unmixing method which is able to sequentially analyze spectral data acquired on a spectrum-by-spectrum basis. After deriving a sequential counterpart of the conventional linear mixing model, the proposed approach recasts the linear unmixing problem into a linear state-space estimation framework. Under Gaussian noise and state models, the estimation of the pure spectra can be efficiently conducted by resorting to Kalman filtering. Interestingly, it is shown that this Kalman filter can operate in a lower-dimensional subspace while ensuring the nonnegativity constraint inherent to pure spectra. This dimensionality reduction allows significantly lightening the computational burden, while leveraging recent advances related to the representation of essential spectral information. The proposed method is evaluated through extensive numerical experiments conducted on synthetic and real Raman data sets. The results show that this Kalman filter-based method offers a convenient trade-off between unmixing accuracy and computational efficiency, which is crucial for operating in an on-the-fly setting. To the best of the authors' knowledge, this is the first operational method which is able to solve the spectral unmixing problem efficiently in a dynamic fashion. It also constitutes a valuable building block for benefiting from acquisition and processing frameworks recently proposed in the microscopy literature, which are motivated by practical issues such as reducing acquisition time and avoiding potential damages being inflicted to photosensitive samples.

RFI-DRUnet: Restoring dynamic spectra corrupted by radio frequency interference -- Application to pulsar observations

Radio frequency interference (RFI) have been an enduring concern in radio astronomy, particularly for the observations of pulsars which require high timing precision and data sensitivity. In most works of the literature, RFI mitigation has been formulated as a detection task that consists of localizing possible RFI in dynamic spectra. This strategy inevitably leads to a potential loss of information since parts of the signal identified as possibly RFI-corrupted are generally not considered in the subsequent data processing pipeline. Conversely, this work proposes to tackle RFI mitigation as a joint detection and restoration that allows parts of the dynamic spectrum affected by RFI to be not only identified but also recovered. The proposed supervised method relies on a deep convolutional network whose architecture inherits the performance reached by a recent yet popular image-denoising network. To train this network, a whole simulation framework is built to generate large data sets according to physics-inspired and statistical models of the pulsar signals and of the RFI. The relevance of the proposed approach is quantitatively assessed by conducting extensive experiments. In particular, the results show that the restored dynamic spectra are sufficiently reliable to estimate pulsar times-of-arrivals with an accuracy close to the one that would be obtained from RFI-free signals.

Regularization by denoising: Bayesian model and Langevin-within-split Gibbs sampling

This paper introduces a Bayesian framework for image inversion by deriving a probabilistic counterpart to the regularization-by-denoising (RED) paradigm. It additionally implements a Monte Carlo algorithm specifically tailored for sampling from the resulting posterior distribution, based on an asymptotically exact data augmentation (AXDA). The proposed algorithm is an approximate instance of split Gibbs sampling (SGS) which embeds one Langevin Monte Carlo step. The proposed method is applied to common imaging tasks such as deblurring, inpainting and super-resolution, demonstrating its efficacy through extensive numerical experiments. These contributions advance Bayesian inference in imaging by leveraging data-driven regularization strategies within a probabilistic framework.

AE-RED: A Hyperspectral Unmixing Framework Powered by Deep Autoencoder and Regularization by Denoising

Spectral unmixing has been extensively studied with a variety of methods and used in many applications. Recently, data-driven techniques with deep learning methods have obtained great attention to spectral unmixing for its superior learning ability to automatically learn the structure information. In particular, autoencoder based architectures are elaborately designed to solve blind unmixing and model complex nonlinear mixtures. Nevertheless, these methods perform unmixing task as blackboxes and lack of interpretability. On the other hand, conventional unmixing methods carefully design the regularizer to add explicit information, in which algorithms such as plug-and-play (PnP) strategies utilize off-the-shelf denoisers to plug powerful priors. In this paper, we propose a generic unmixing framework to integrate the autoencoder network with regularization by denoising (RED), named AE-RED. More specially, we decompose the unmixing optimized problem into two subproblems. The first one is solved using deep autoencoders to implicitly regularize the estimates and model the mixture mechanism. The second one leverages the denoiser to bring in the explicit information. In this way, both the characteristics of the deep autoencoder based unmixing methods and priors provided by denoisers are merged into our well-designed framework to enhance the unmixing performance. Experiment results on both synthetic and real data sets show the superiority of our proposed framework compared with state-of-the-art unmixing approaches.

Guided Deep Generative Model-based Spatial Regularization for Multiband Imaging Inverse Problems

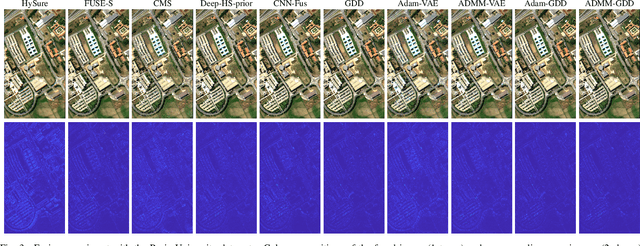
When adopting a model-based formulation, solving inverse problems encountered in multiband imaging requires to define spatial and spectral regularizations. In most of the works of the literature, spectral information is extracted from the observations directly to derive data-driven spectral priors. Conversely, the choice of the spatial regularization often boils down to the use of conventional penalizations (e.g., total variation) promoting expected features of the reconstructed image (e.g., piecewise constant). In this work, we propose a generic framework able to capitalize on an auxiliary acquisition of high spatial resolution to derive tailored data-driven spatial regularizations. This approach leverages on the ability of deep learning to extract high level features. More precisely, the regularization is conceived as a deep generative network able to encode spatial semantic features contained in this auxiliary image of high spatial resolution. To illustrate the versatility of this approach, it is instantiated to conduct two particular tasks, namely multiband image fusion and multiband image inpainting. Experimental results obtained on these two tasks demonstrate the benefit of this class of informed regularizations when compared to more conventional ones.

Normalizing flow sampling with Langevin dynamics in the latent space

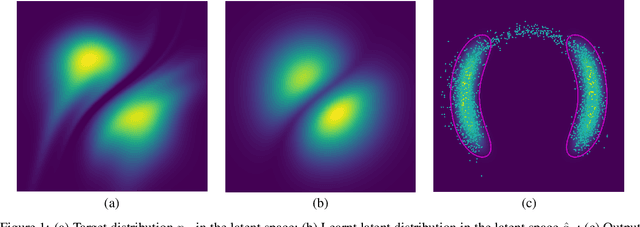
Normalizing flows (NF) use a continuous generator to map a simple latent (e.g. Gaussian) distribution, towards an empirical target distribution associated with a training data set. Once trained by minimizing a variational objective, the learnt map provides an approximate generative model of the target distribution. Since standard NF implement differentiable maps, they may suffer from pathological behaviors when targeting complex distributions. For instance, such problems may appear for distributions on multi-component topologies or characterized by multiple modes with high probability regions separated by very unlikely areas. A typical symptom is the explosion of the Jacobian norm of the transformation in very low probability areas. This paper proposes to overcome this issue thanks to a new Markov chain Monte Carlo algorithm to sample from the target distribution in the latent domain before transporting it back to the target domain. The approach relies on a Metropolis adjusted Langevin algorithm (MALA) whose dynamics explicitly exploits the Jacobian of the transformation. Contrary to alternative approaches, the proposed strategy preserves the tractability of the likelihood and it does not require a specific training. Notably, it can be straightforwardly used with any pre-trained NF network, regardless of the architecture. Experiments conducted on synthetic and high-dimensional real data sets illustrate the efficiency of the method.

Plug-and-Play split Gibbs sampler: embedding deep generative priors in Bayesian inference

This paper introduces a stochastic plug-and-play (PnP) sampling algorithm that leverages variable splitting to efficiently sample from a posterior distribution. The algorithm based on split Gibbs sampling (SGS) draws inspiration from the alternating direction method of multipliers (ADMM). It divides the challenging task of posterior sampling into two simpler sampling problems. The first problem depends on the likelihood function, while the second is interpreted as a Bayesian denoising problem that can be readily carried out by a deep generative model. Specifically, for an illustrative purpose, the proposed method is implemented in this paper using state-of-the-art diffusion-based generative models. Akin to its deterministic PnP-based counterparts, the proposed method exhibits the great advantage of not requiring an explicit choice of the prior distribution, which is rather encoded into a pre-trained generative model. However, unlike optimization methods (e.g., PnP-ADMM) which generally provide only point estimates, the proposed approach allows conventional Bayesian estimators to be accompanied by confidence intervals at a reasonable additional computational cost. Experiments on commonly studied image processing problems illustrate the efficiency of the proposed sampling strategy. Its performance is compared to recent state-of-the-art optimization and sampling methods.

Probabilistic Simplex Component Analysis by Importance Sampling

In this paper we consider the problem of linear unmixing hidden random variables defined over the simplex with additive Gaussian noise, also known as probabilistic simplex component analysis (PRISM). Previous solutions to tackle this challenging problem were based on geometrical approaches or computationally intensive variational methods. In contrast, we propose a conventional expectation maximization (EM) algorithm which embeds importance sampling. For this purpose, the proposal distribution is chosen as a simple surrogate distribution of the target posterior that is guaranteed to lie in the simplex. This distribution is based on the Gaussian linear minimum mean squared error (LMMSE) approximation which is accurate at high signal-to-noise ratio. Numerical experiments in different settings demonstrate the advantages of this adaptive surrogate over state-of-the-art methods.