Multitask Learning with Stochastic Interpolants

We propose a framework for learning maps between probability distributions that broadly generalizes the time dynamics of flow and diffusion models. To enable this, we generalize stochastic interpolants by replacing the scalar time variable with vectors, matrices, or linear operators, allowing us to bridge probability distributions across multiple dimensional spaces. This approach enables the construction of versatile generative models capable of fulfilling multiple tasks without task-specific training. Our operator-based interpolants not only provide a unifying theoretical perspective for existing generative models but also extend their capabilities. Through numerical experiments, we demonstrate the zero-shot efficacy of our method on conditional generation and inpainting, fine-tuning and posterior sampling, and multiscale modeling, suggesting its potential as a generic task-agnostic alternative to specialized models.

Normalizing flow sampling with Langevin dynamics in the latent space

Normalizing flows (NF) use a continuous generator to map a simple latent (e.g. Gaussian) distribution, towards an empirical target distribution associated with a training data set. Once trained by minimizing a variational objective, the learnt map provides an approximate generative model of the target distribution. Since standard NF implement differentiable maps, they may suffer from pathological behaviors when targeting complex distributions. For instance, such problems may appear for distributions on multi-component topologies or characterized by multiple modes with high probability regions separated by very unlikely areas. A typical symptom is the explosion of the Jacobian norm of the transformation in very low probability areas. This paper proposes to overcome this issue thanks to a new Markov chain Monte Carlo algorithm to sample from the target distribution in the latent domain before transporting it back to the target domain. The approach relies on a Metropolis adjusted Langevin algorithm (MALA) whose dynamics explicitly exploits the Jacobian of the transformation. Contrary to alternative approaches, the proposed strategy preserves the tractability of the likelihood and it does not require a specific training. Notably, it can be straightforwardly used with any pre-trained NF network, regardless of the architecture. Experiments conducted on synthetic and high-dimensional real data sets illustrate the efficiency of the method.

Plug-and-Play split Gibbs sampler: embedding deep generative priors in Bayesian inference

This paper introduces a stochastic plug-and-play (PnP) sampling algorithm that leverages variable splitting to efficiently sample from a posterior distribution. The algorithm based on split Gibbs sampling (SGS) draws inspiration from the alternating direction method of multipliers (ADMM). It divides the challenging task of posterior sampling into two simpler sampling problems. The first problem depends on the likelihood function, while the second is interpreted as a Bayesian denoising problem that can be readily carried out by a deep generative model. Specifically, for an illustrative purpose, the proposed method is implemented in this paper using state-of-the-art diffusion-based generative models. Akin to its deterministic PnP-based counterparts, the proposed method exhibits the great advantage of not requiring an explicit choice of the prior distribution, which is rather encoded into a pre-trained generative model. However, unlike optimization methods (e.g., PnP-ADMM) which generally provide only point estimates, the proposed approach allows conventional Bayesian estimators to be accompanied by confidence intervals at a reasonable additional computational cost. Experiments on commonly studied image processing problems illustrate the efficiency of the proposed sampling strategy. Its performance is compared to recent state-of-the-art optimization and sampling methods.

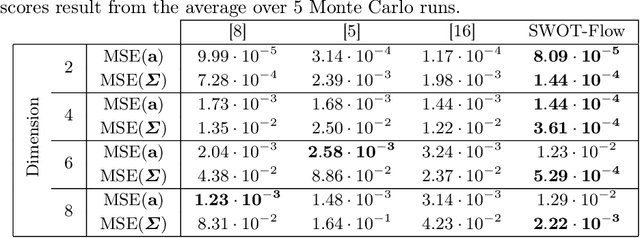
Sliced-Wasserstein normalizing flows: beyond maximum likelihood training

Despite their advantages, normalizing flows generally suffer from several shortcomings including their tendency to generate unrealistic data (e.g., images) and their failing to detect out-of-distribution data. One reason for these deficiencies lies in the training strategy which traditionally exploits a maximum likelihood principle only. This paper proposes a new training paradigm based on a hybrid objective function combining the maximum likelihood principle (MLE) and a sliced-Wasserstein distance. Results obtained on synthetic toy examples and real image data sets show better generative abilities in terms of both likelihood and visual aspects of the generated samples. Reciprocally, the proposed approach leads to a lower likelihood of out-of-distribution data, demonstrating a greater data fidelity of the resulting flows.

Learning Optimal Transport Between two Empirical Distributions with Normalizing Flows

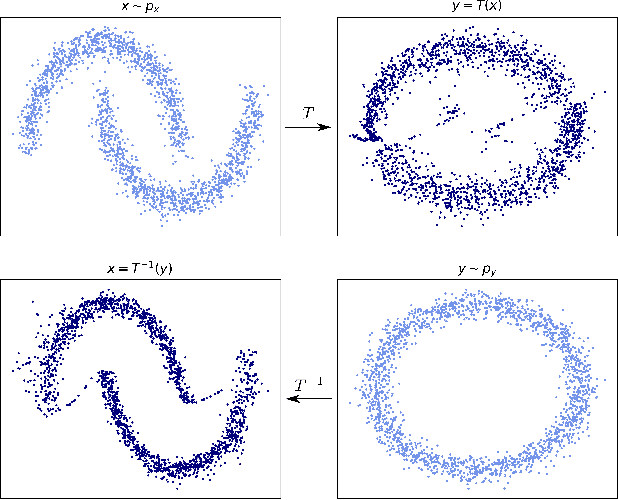
Optimal transport (OT) provides effective tools for comparing and mapping probability measures. We propose to leverage the flexibility of neural networks to learn an approximate optimal transport map. More precisely, we present a new and original method to address the problem of transporting a finite set of samples associated with a first underlying unknown distribution towards another finite set of samples drawn from another unknown distribution. We show that a particular instance of invertible neural networks, namely the normalizing flows, can be used to approximate the solution of this OT problem between a pair of empirical distributions. To this aim, we propose to relax the Monge formulation of OT by replacing the equality constraint on the push-forward measure by the minimization of the corresponding Wasserstein distance. The push-forward operator to be retrieved is then restricted to be a normalizing flow which is trained by optimizing the resulting cost function. This approach allows the transport map to be discretized as a composition of functions. Each of these functions is associated to one sub-flow of the network, whose output provides intermediate steps of the transport between the original and target measures. This discretization yields also a set of intermediate barycenters between the two measures of interest. Experiments conducted on toy examples as well as a challenging task of unsupervised translation demonstrate the interest of the proposed method. Finally, some experiments show that the proposed approach leads to a good approximation of the true OT.