Learning Optimal Transport Between two Empirical Distributions with Normalizing Flows
Paper and Code
Jul 05, 2022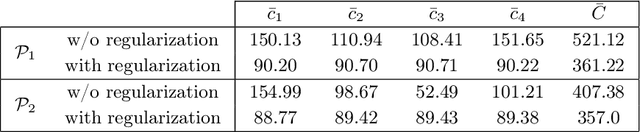
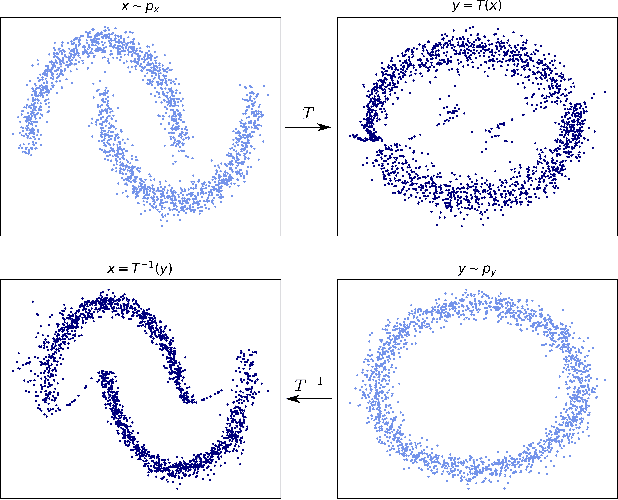
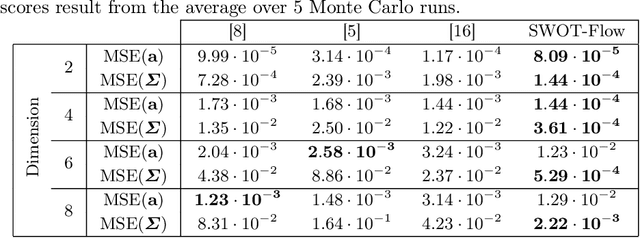

Optimal transport (OT) provides effective tools for comparing and mapping probability measures. We propose to leverage the flexibility of neural networks to learn an approximate optimal transport map. More precisely, we present a new and original method to address the problem of transporting a finite set of samples associated with a first underlying unknown distribution towards another finite set of samples drawn from another unknown distribution. We show that a particular instance of invertible neural networks, namely the normalizing flows, can be used to approximate the solution of this OT problem between a pair of empirical distributions. To this aim, we propose to relax the Monge formulation of OT by replacing the equality constraint on the push-forward measure by the minimization of the corresponding Wasserstein distance. The push-forward operator to be retrieved is then restricted to be a normalizing flow which is trained by optimizing the resulting cost function. This approach allows the transport map to be discretized as a composition of functions. Each of these functions is associated to one sub-flow of the network, whose output provides intermediate steps of the transport between the original and target measures. This discretization yields also a set of intermediate barycenters between the two measures of interest. Experiments conducted on toy examples as well as a challenging task of unsupervised translation demonstrate the interest of the proposed method. Finally, some experiments show that the proposed approach leads to a good approximation of the true OT.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge