Dictionary Learning with Low-rank Coding Coefficients for Tensor Completion
Paper and Code
Sep 26, 2020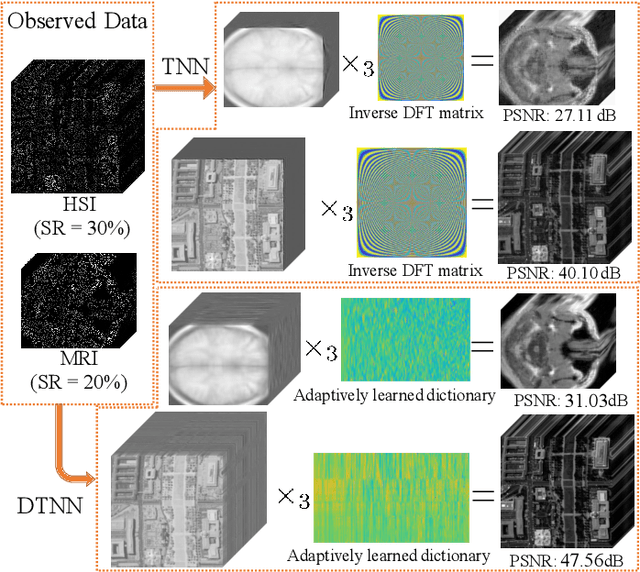


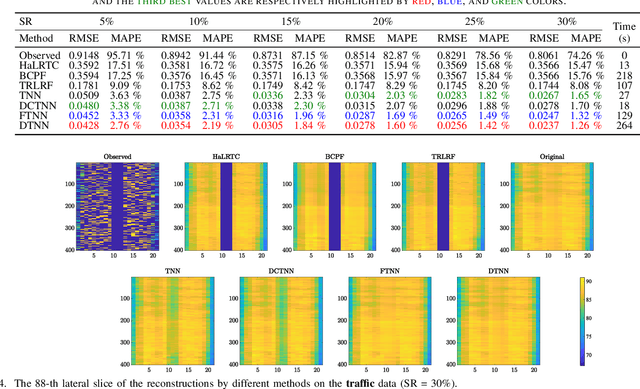
In this paper, we propose a novel tensor learning and coding model for third-order data completion. Our model is to learn a data-adaptive dictionary from the given observations, and determine the coding coefficients of third-order tensor tubes. In the completion process, we minimize the low-rankness of each tensor slice containing the coding coefficients. By comparison with the traditional pre-defined transform basis, the advantages of the proposed model are that (i) the dictionary can be learned based on the given data observations so that the basis can be more adaptively and accurately constructed, and (ii) the low-rankness of the coding coefficients can allow the linear combination of dictionary features more effectively. Also we develop a multi-block proximal alternating minimization algorithm for solving such tensor learning and coding model, and show that the sequence generated by the algorithm can globally converge to a critical point. Extensive experimental results for real data sets such as videos, hyperspectral images, and traffic data are reported to demonstrate these advantages and show the performance of the proposed tensor learning and coding method is significantly better than the other tensor completion methods in terms of several evaluation metrics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge