AgentThink: A Unified Framework for Tool-Augmented Chain-of-Thought Reasoning in Vision-Language Models for Autonomous Driving

Vision-Language Models (VLMs) show promise for autonomous driving, yet their struggle with hallucinations, inefficient reasoning, and limited real-world validation hinders accurate perception and robust step-by-step reasoning. To overcome this, we introduce \textbf{AgentThink}, a pioneering unified framework that, for the first time, integrates Chain-of-Thought (CoT) reasoning with dynamic, agent-style tool invocation for autonomous driving tasks. AgentThink's core innovations include: \textbf{(i) Structured Data Generation}, by establishing an autonomous driving tool library to automatically construct structured, self-verified reasoning data explicitly incorporating tool usage for diverse driving scenarios; \textbf{(ii) A Two-stage Training Pipeline}, employing Supervised Fine-Tuning (SFT) with Group Relative Policy Optimization (GRPO) to equip VLMs with the capability for autonomous tool invocation; and \textbf{(iii) Agent-style Tool-Usage Evaluation}, introducing a novel multi-tool assessment protocol to rigorously evaluate the model's tool invocation and utilization. Experiments on the DriveLMM-o1 benchmark demonstrate AgentThink significantly boosts overall reasoning scores by \textbf{53.91\%} and enhances answer accuracy by \textbf{33.54\%}, while markedly improving reasoning quality and consistency. Furthermore, ablation studies and robust zero-shot/few-shot generalization experiments across various benchmarks underscore its powerful capabilities. These findings highlight a promising trajectory for developing trustworthy and tool-aware autonomous driving models.

Large Language Models for Data Synthesis

Generating synthetic data that faithfully captures the statistical structure of real-world distributions is a fundamental challenge in data modeling. Classical approaches often depend on strong parametric assumptions or manual structural design and struggle in high-dimensional or heterogeneous domains. Recent progress in Large Language Models (LLMs) reveals their potential as flexible, high-dimensional priors over real-world distributions. However, when applied to data synthesis, standard LLM-based sampling is inefficient, constrained by fixed context limits, and fails to ensure statistical alignment. Given this, we introduce LLMSynthor, a general framework for data synthesis that transforms LLMs into structure-aware simulators guided by distributional feedback. LLMSynthor treats the LLM as a nonparametric copula simulator for modeling high-order dependencies and introduces LLM Proposal Sampling to generate grounded proposal distributions that improve sampling efficiency without requiring rejection. By minimizing discrepancies in the summary statistics space, the iterative synthesis loop aligns real and synthetic data while gradually uncovering and refining the latent generative structure. We evaluate LLMSynthor in both controlled and real-world settings using heterogeneous datasets in privacy-sensitive domains (e.g., e-commerce, population, and mobility) that encompass both structured and unstructured formats. The synthetic data produced by LLMSynthor shows high statistical fidelity, practical utility, and cross-data adaptability, positioning it as a valuable tool across economics, social science, urban studies, and beyond.

Nearest Neighbor Multivariate Time Series Forecasting

Multivariate time series (MTS) forecasting has a wide range of applications in both industry and academia. Recently, spatial-temporal graph neural networks (STGNNs) have gained popularity as MTS forecasting methods. However, current STGNNs can only use the finite length of MTS input data due to the computational complexity. Moreover, they lack the ability to identify similar patterns throughout the entire dataset and struggle with data that exhibit sparsely and discontinuously distributed correlations among variables over an extensive historical period, resulting in only marginal improvements. In this article, we introduce a simple yet effective k-nearest neighbor MTS forecasting ( kNN-MTS) framework, which forecasts with a nearest neighbor retrieval mechanism over a large datastore of cached series, using representations from the MTS model for similarity search. This approach requires no additional training and scales to give the MTS model direct access to the whole dataset at test time, resulting in a highly expressive model that consistently improves performance, and has the ability to extract sparse distributed but similar patterns spanning over multivariables from the entire dataset. Furthermore, a hybrid spatial-temporal encoder (HSTEncoder) is designed for kNN-MTS which can capture both long-term temporal and short-term spatial-temporal dependencies and is shown to provide accurate representation for kNN-MTSfor better forecasting. Experimental results on several real-world datasets show a significant improvement in the forecasting performance of kNN-MTS. The quantitative analysis also illustrates the interpretability and efficiency of kNN-MTS, showing better application prospects and opening up a new path for efficiently using the large dataset in MTS models.

Preference Optimization for Combinatorial Optimization Problems

Reinforcement Learning (RL) has emerged as a powerful tool for neural combinatorial optimization, enabling models to learn heuristics that solve complex problems without requiring expert knowledge. Despite significant progress, existing RL approaches face challenges such as diminishing reward signals and inefficient exploration in vast combinatorial action spaces, leading to inefficiency. In this paper, we propose Preference Optimization, a novel method that transforms quantitative reward signals into qualitative preference signals via statistical comparison modeling, emphasizing the superiority among sampled solutions. Methodologically, by reparameterizing the reward function in terms of policy and utilizing preference models, we formulate an entropy-regularized RL objective that aligns the policy directly with preferences while avoiding intractable computations. Furthermore, we integrate local search techniques into the fine-tuning rather than post-processing to generate high-quality preference pairs, helping the policy escape local optima. Empirical results on various benchmarks, such as the Traveling Salesman Problem (TSP), the Capacitated Vehicle Routing Problem (CVRP) and the Flexible Flow Shop Problem (FFSP), demonstrate that our method significantly outperforms existing RL algorithms, achieving superior convergence efficiency and solution quality.

Likelihood-Free Variational Autoencoders

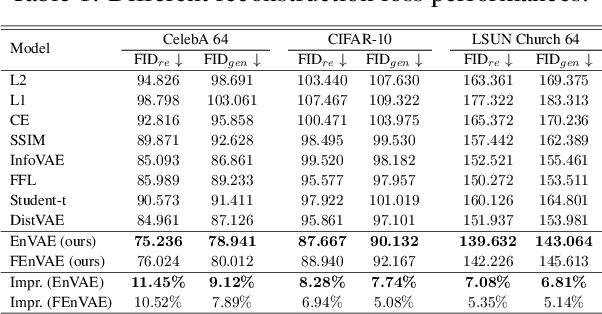
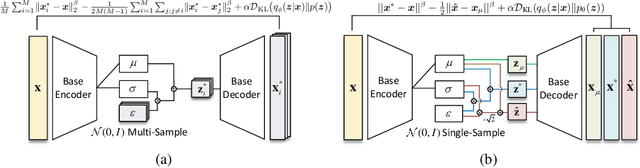
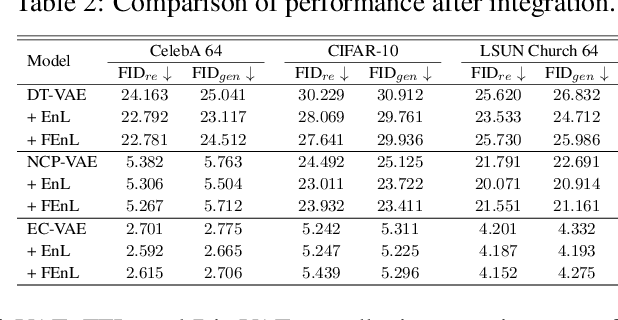
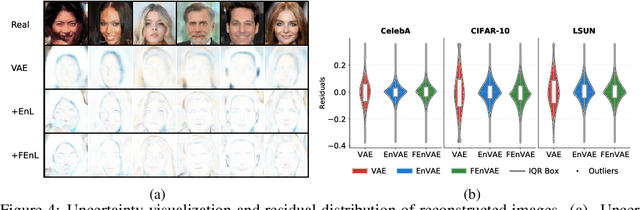
Variational Autoencoders (VAEs) typically rely on a probabilistic decoder with a predefined likelihood, most commonly an isotropic Gaussian, to model the data conditional on latent variables. While convenient for optimization, this choice often leads to likelihood misspecification, resulting in blurry reconstructions and poor data fidelity, especially for high-dimensional data such as images. In this work, we propose \textit{EnVAE}, a novel likelihood-free generative framework that has a deterministic decoder and employs the energy score -- a proper scoring rule -- to build the reconstruction loss. This enables likelihood-free inference without requiring explicit parametric density functions. To address the computational inefficiency of the energy score, we introduce a fast variant, \textit{FEnVAE}, based on the local smoothness of the decoder and the sharpness of the posterior distribution of latent variables. This yields an efficient single-sample training objective that integrates seamlessly into existing VAE pipelines with minimal overhead. Empirical results on standard benchmarks demonstrate that \textit{EnVAE} achieves superior reconstruction and generation quality compared to likelihood-based baselines. Our framework offers a general, scalable, and statistically principled alternative for flexible and nonparametric distribution learning in generative modeling.

Multi-Agent Coordination across Diverse Applications: A Survey

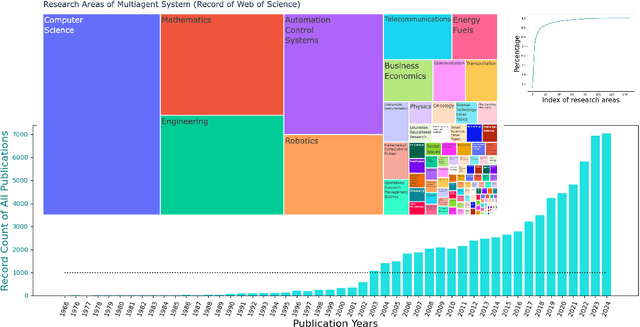
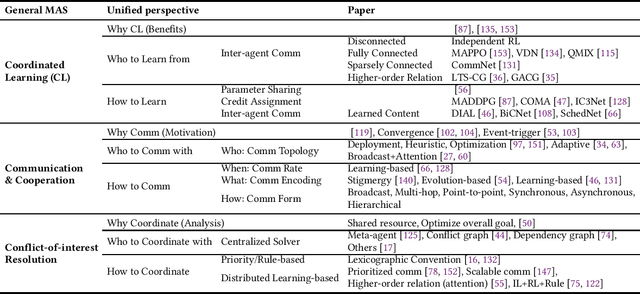
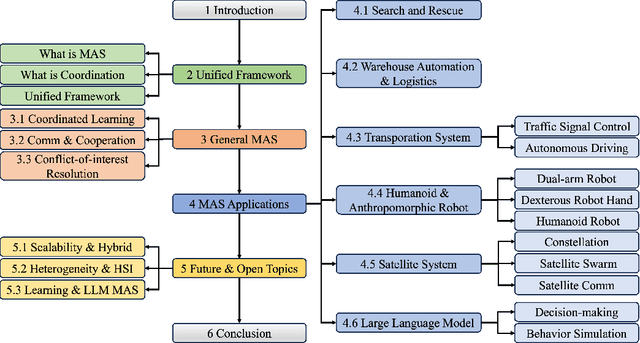
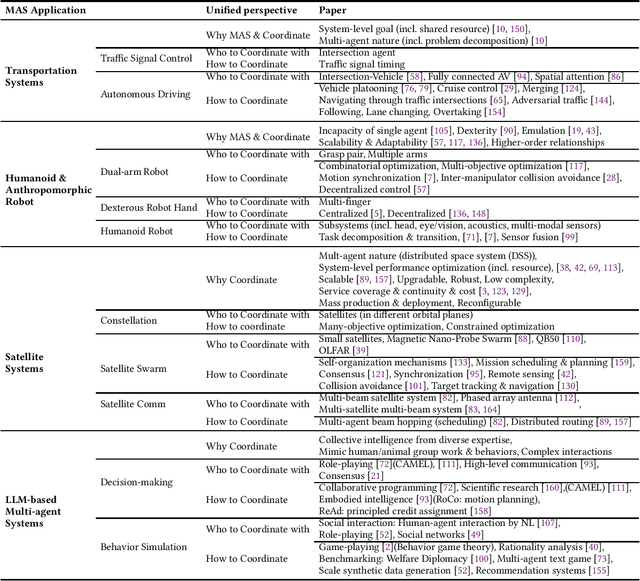
Multi-agent coordination studies the underlying mechanism enabling the trending spread of diverse multi-agent systems (MAS) and has received increasing attention, driven by the expansion of emerging applications and rapid AI advances. This survey outlines the current state of coordination research across applications through a unified understanding that answers four fundamental coordination questions: (1) what is coordination; (2) why coordination; (3) who to coordinate with; and (4) how to coordinate. Our purpose is to explore existing ideas and expertise in coordination and their connections across diverse applications, while identifying and highlighting emerging and promising research directions. First, general coordination problems that are essential to varied applications are identified and analyzed. Second, a number of MAS applications are surveyed, ranging from widely studied domains, e.g., search and rescue, warehouse automation and logistics, and transportation systems, to emerging fields including humanoid and anthropomorphic robots, satellite systems, and large language models (LLMs). Finally, open challenges about the scalability, heterogeneity, and learning mechanisms of MAS are analyzed and discussed. In particular, we identify the hybridization of hierarchical and decentralized coordination, human-MAS coordination, and LLM-based MAS as promising future directions.

Adversarial Vulnerabilities in Large Language Models for Time Series Forecasting

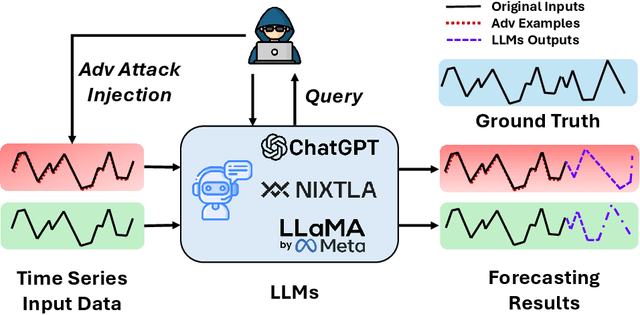
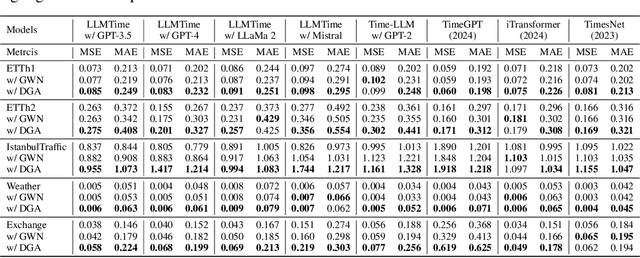
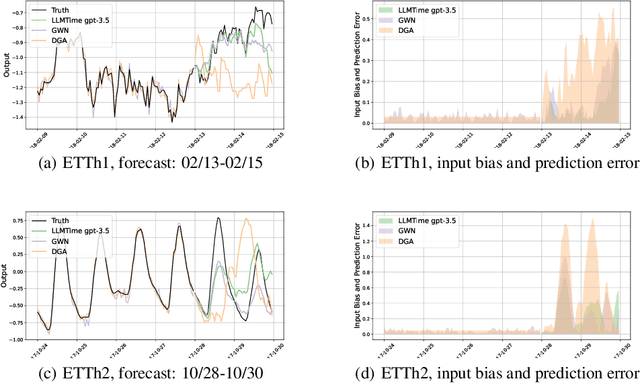
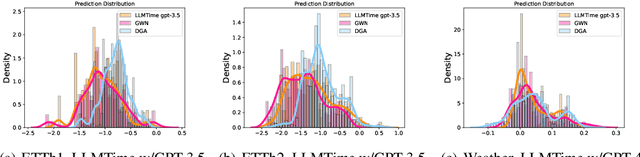
Large Language Models (LLMs) have recently demonstrated significant potential in the field of time series forecasting, offering impressive capabilities in handling complex temporal data. However, their robustness and reliability in real-world applications remain under-explored, particularly concerning their susceptibility to adversarial attacks. In this paper, we introduce a targeted adversarial attack framework for LLM-based time series forecasting. By employing both gradient-free and black-box optimization methods, we generate minimal yet highly effective perturbations that significantly degrade the forecasting accuracy across multiple datasets and LLM architectures. Our experiments, which include models like TimeGPT and LLM-Time with GPT-3.5, GPT-4, LLaMa, and Mistral, show that adversarial attacks lead to much more severe performance degradation than random noise, and demonstrate the broad effectiveness of our attacks across different LLMs. The results underscore the critical vulnerabilities of LLMs in time series forecasting, highlighting the need for robust defense mechanisms to ensure their reliable deployment in practical applications.

Generalized Least Squares Kernelized Tensor Factorization

Real-world datasets often contain missing or corrupted values. Completing multidimensional tensor-structured data with missing entries is essential for numerous applications. Smoothness-constrained low-rank factorization models have shown superior performance with reduced computational costs. While effective at capturing global and long-range correlations, these models struggle to reproduce short-scale, high-frequency variations in the data. In this paper, we introduce the \Generalized Least Squares Kernelized Tensor Factorization (GLSKF) framework for tensor completion. GLSKF integrates smoothness-constrained low-rank factorization with a locally correlated residual process; the resulting additive structure can effectively characterize both global dependencies and local variations. In particular, we define the covariance norm to enforce the smoothness of factor matrices in the global low-rank factorization, and use structured covariance/kernel functions to model the local processes. For model estimation, we develop an alternating least squares (ALS) procedure with closed-form solutions for each subproblem. To efficiently handle missing data, GLSKF utilizes projection matrices that preserve the Kronecker structure of covariances, facilitating fast computations through conjugate gradient (CG) and preconditioned conjugate gradient (PCG) algorithms. The proposed framework is evaluated on four real-world datasets across diverse tasks: traffic speed imputation, color image inpainting, video completion, and MRI image reconstruction. Experimental results confirm that GLSKF delivers superior effectiveness and scalability, establishing it as a robust solution for multidimensional tensor completion.

SPTTE: A Spatiotemporal Probabilistic Framework for Travel Time Estimation

Accurate travel time estimation is essential for navigation and itinerary planning. While existing research employs probabilistic modeling to assess travel time uncertainty and account for correlations between multiple trips, modeling the temporal variability of multi-trip travel time distributions remains a significant challenge. Capturing the evolution of joint distributions requires large, well-organized datasets; however, real-world trip data are often temporally sparse and spatially unevenly distributed. To address this issue, we propose SPTTE, a spatiotemporal probabilistic framework that models the evolving joint distribution of multi-trip travel times by formulating the estimation task as a spatiotemporal stochastic process regression problem with fragmented observations. SPTTE incorporates an RNN-based temporal Gaussian process parameterization to regularize sparse observations and capture temporal dependencies. Additionally, it employs a prior-based heterogeneity smoothing strategy to correct unreliable learning caused by unevenly distributed trips, effectively modeling temporal variability under sparse and uneven data distributions. Evaluations on real-world datasets demonstrate that SPTTE outperforms state-of-the-art deterministic and probabilistic methods by over 10.13%. Ablation studies and visualizations further confirm the effectiveness of the model components.

MVG-CRPS: A Robust Loss Function for Multivariate Probabilistic Forecasting

In probabilistic time series forecasting, the multivariate Gaussian (MVG) distribution is widely used as predictive distribution for correlated continuous random variables. Current deep probabilistic models typically employ neural networks to parameterize the mean vector and covariance matrix of the distribution, with log-score (i.e., negative log-likelihood) as the default loss function. However, log-score is highly sensitive to outliers, leading to significant errors when anomalies are present in the data. Motivated by the use of the continuous ranked probability score (CRPS) in learning univariate distributions, we propose a robust loss function specifically designed for high-dimensional MVG outputs. The proposed MVG-CRPS loss function has a closed-form expression based on the neural network outputs, making it easily integrable into deep learning models. We evaluate MVG-CRPS on two probabilistic forecasting tasks -- multivariate autoregressive and univariate sequence-to-sequence (Seq2Seq) forecasting -- both involving observations following MVG distribution. Experimental results on real-world datasets demonstrate that MVG-CRPS achieves both robustness and efficiency, offering enhanced accuracy and uncertainty quantification in probabilistic forecasting.