Bayesian Kernelized Tensor Factorization as Surrogate for Bayesian Optimization

Bayesian optimization (BO) primarily uses Gaussian processes (GP) as the key surrogate model, mostly with a simple stationary and separable kernel function such as the widely used squared-exponential kernel with automatic relevance determination (SE-ARD). However, such simple kernel specifications are deficient in learning functions with complex features, such as being nonstationary, nonseparable, and multimodal. Approximating such functions using a local GP, even in a low-dimensional space, will require a large number of samples, not to mention in a high-dimensional setting. In this paper, we propose to use Bayesian Kernelized Tensor Factorization (BKTF) -- as a new surrogate model -- for BO in a D-dimensional Cartesian product space. Our key idea is to approximate the underlying D-dimensional solid with a fully Bayesian low-rank tensor CP decomposition, in which we place GP priors on the latent basis functions for each dimension to encode local consistency and smoothness. With this formulation, information from each sample can be shared not only with neighbors but also across dimensions. Although BKTF no longer has an analytical posterior, we can still efficiently approximate the posterior distribution through Markov chain Monte Carlo (MCMC) and obtain prediction and full uncertainty quantification (UQ). We conduct numerical experiments on both standard BO testing problems and machine learning hyperparameter tuning problems, and our results confirm the superiority of BKTF in terms of sample efficiency.

Bayesian Complementary Kernelized Learning for Multidimensional Spatiotemporal Data

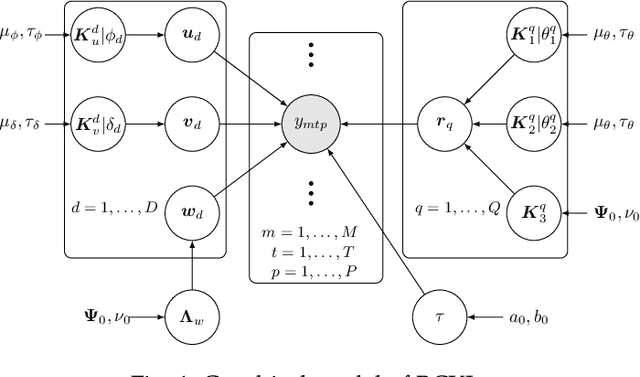
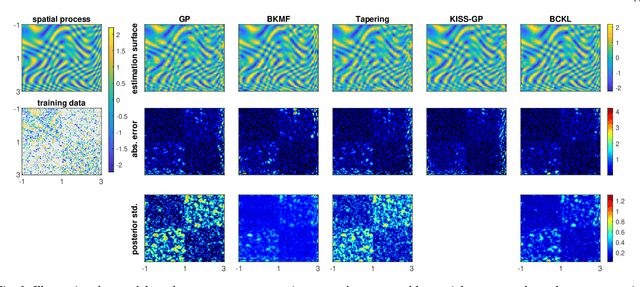
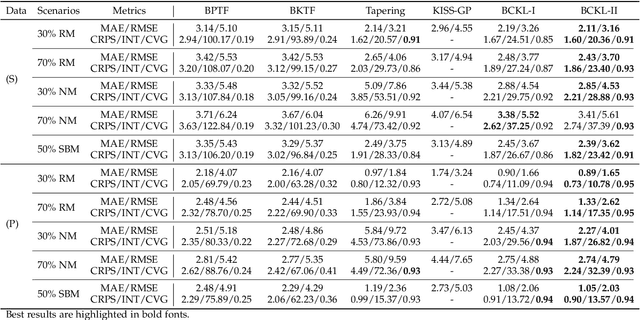
Probabilistic modeling of multidimensional spatiotemporal data is critical to many real-world applications. However, real-world spatiotemporal data often exhibits complex dependencies that are nonstationary, i.e., correlation structure varies with location/time, and nonseparable, i.e., dependencies exist between space and time. Developing effective and computationally efficient statistical models to accommodate nonstationary/nonseparable processes containing both long-range and short-scale variations becomes a challenging task, especially for large-scale datasets with various corruption/missing structures. In this paper, we propose a new statistical framework -- Bayesian Complementary Kernelized Learning (BCKL) -- to achieve scalable probabilistic modeling for multidimensional spatiotemporal data. To effectively describe complex dependencies, BCKL integrates kernelized low-rank factorization with short-range spatiotemporal Gaussian processes (GP), in which the two components complement each other. Specifically, we use a multi-linear low-rank factorization component to capture the global/long-range correlations in the data and introduce an additive short-scale GP based on compactly supported kernel functions to characterize the remaining local variabilities. We develop an efficient Markov chain Monte Carlo (MCMC) algorithm for model inference and evaluate the proposed BCKL framework on both synthetic and real-world spatiotemporal datasets. Our results confirm the superior performance of BCKL in providing accurate posterior mean and high-quality uncertainty estimates.

Spatial Aggregation and Temporal Convolution Networks for Real-time Kriging

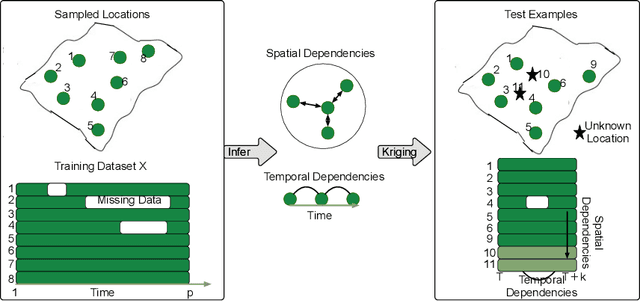
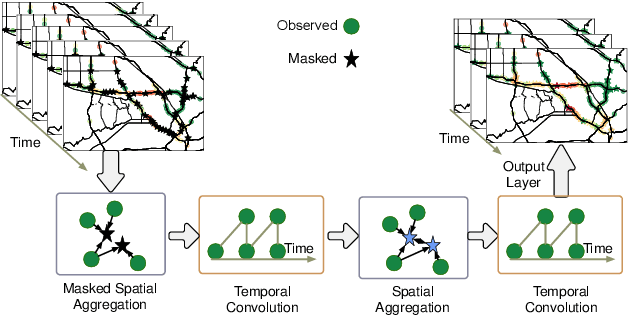
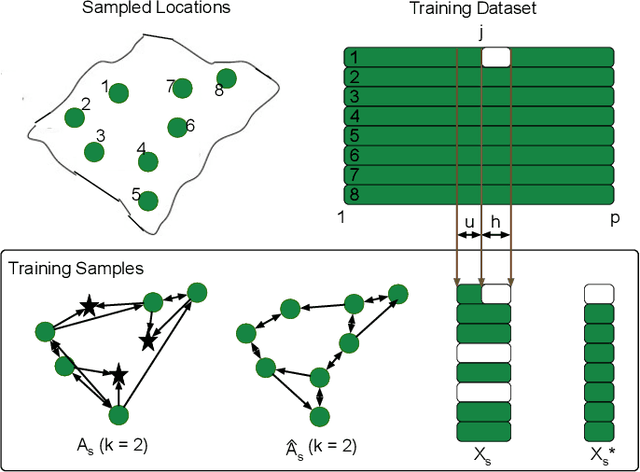
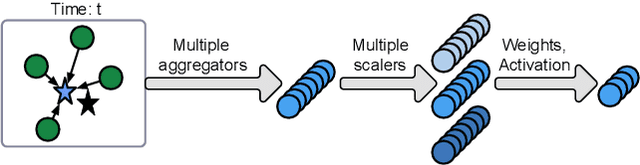
Spatiotemporal kriging is an important application in spatiotemporal data analysis, aiming to recover/interpolate signals for unsampled/unobserved locations based on observed signals. The principle challenge for spatiotemporal kriging is how to effectively model and leverage the spatiotemporal dependencies within the data. Recently, graph neural networks (GNNs) have shown great promise for spatiotemporal kriging tasks. However, standard GNNs often require a carefully designed adjacency matrix and specific aggregation functions, which are inflexible for general applications/problems. To address this issue, we present SATCN -- Spatial Aggregation and Temporal Convolution Networks -- a universal and flexible framework to perform spatiotemporal kriging for various spatiotemporal datasets without the need for model specification. Specifically, we propose a novel spatial aggregation network (SAN) inspired by Principal Neighborhood Aggregation, which uses multiple aggregation functions to help one node gather diverse information from its neighbors. To exclude information from unsampled nodes, a masking strategy that prevents the unsampled sensors from sending messages to their neighborhood is introduced to SAN. We capture temporal dependencies by the temporal convolutional networks, which allows our model to cope with data of diverse sizes. To make SATCN generalizable to unseen nodes and even unseen graph structures, we employ an inductive strategy to train SATCN. We conduct extensive experiments on three real-world spatiotemporal datasets, including traffic speed and climate recordings. Our results demonstrate the superiority of SATCN over traditional and GNN-based kriging models.

Scalable Spatiotemporally Varying Coefficient Modeling with Bayesian Kernelized Tensor Regression

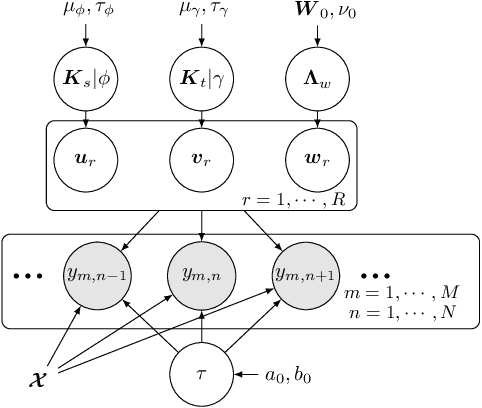
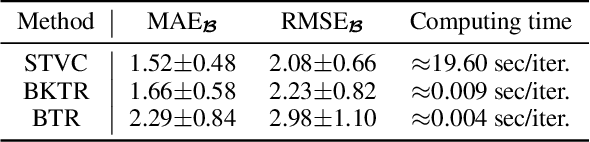
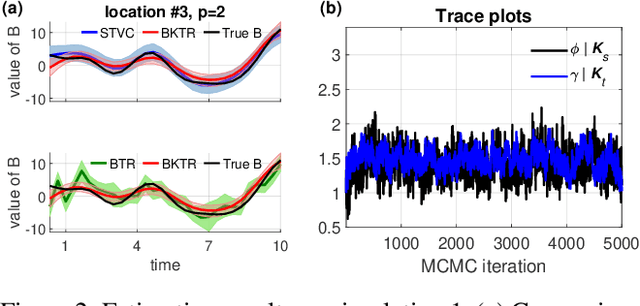
As a regression technique in spatial statistics, spatiotemporally varying coefficient model (STVC) is an important tool to discover nonstationary and interpretable response-covariate associations over both space and time. However, it is difficult to apply STVC for large-scale spatiotemporal analysis due to the high computational cost. To address this challenge, we summarize the spatiotemporally varying coefficients using a third-order tensor structure and propose to reformulate the spatiotemporally varying coefficient model as a special low-rank tensor regression problem. The low-rank decomposition can effectively model the global patterns of the large data with substantially reduced number of parameters. To further incorporate the local spatiotemporal dependencies among the samples, we place Gaussian process (GP) priors on the spatial and temporal factor matrices to better encode local spatial and temporal processes on each factor component. We refer to the overall framework as Bayesian Kernelized Tensor Regression (BKTR). For model inference, we develop an efficient Markov chain Monte Carlo (MCMC) algorithm, which uses Gibbs sampling to update factor matrices and slice sampling to update kernel hyperparameters. We conduct extensive experiments on both synthetic and real-world data sets, and our results confirm the superior performance and efficiency of BKTR for model estimation and parameter inference.

Low-Rank Autoregressive Tensor Completion for Spatiotemporal Traffic Data Imputation

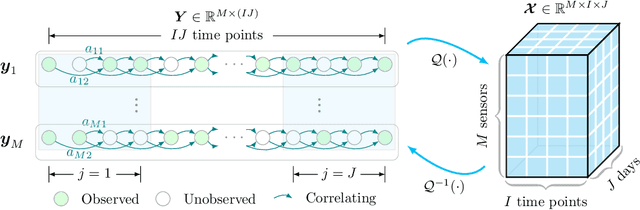
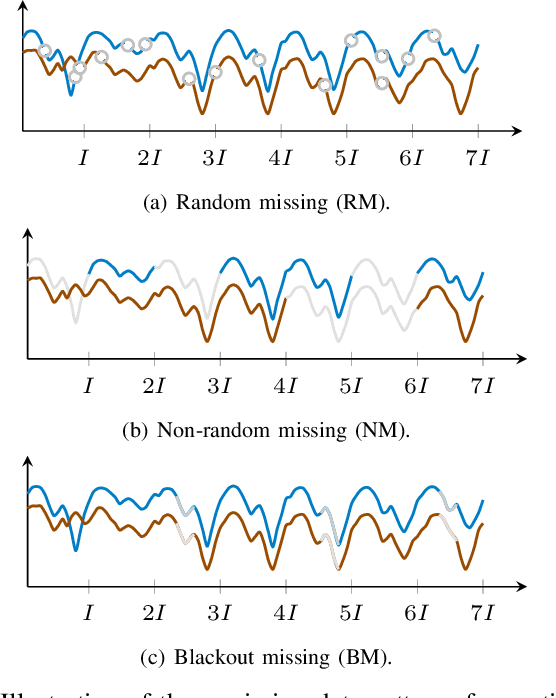
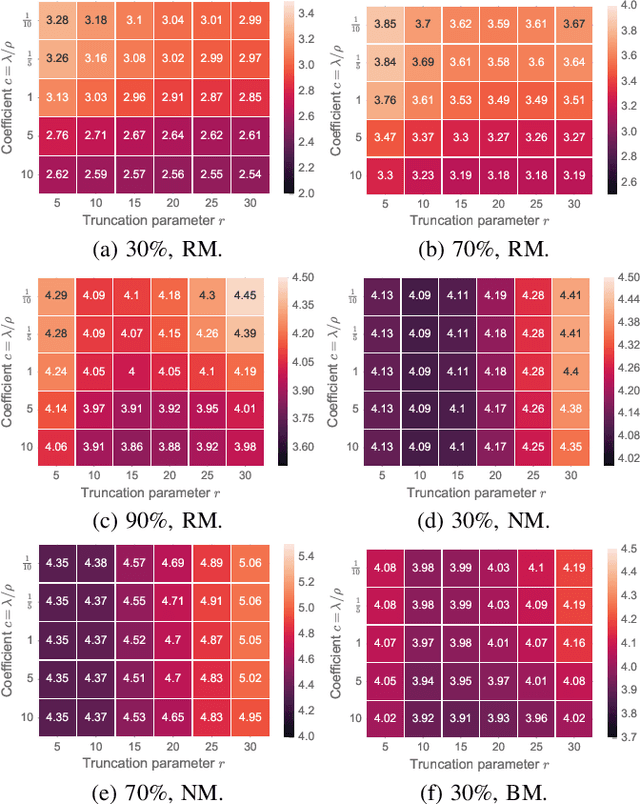
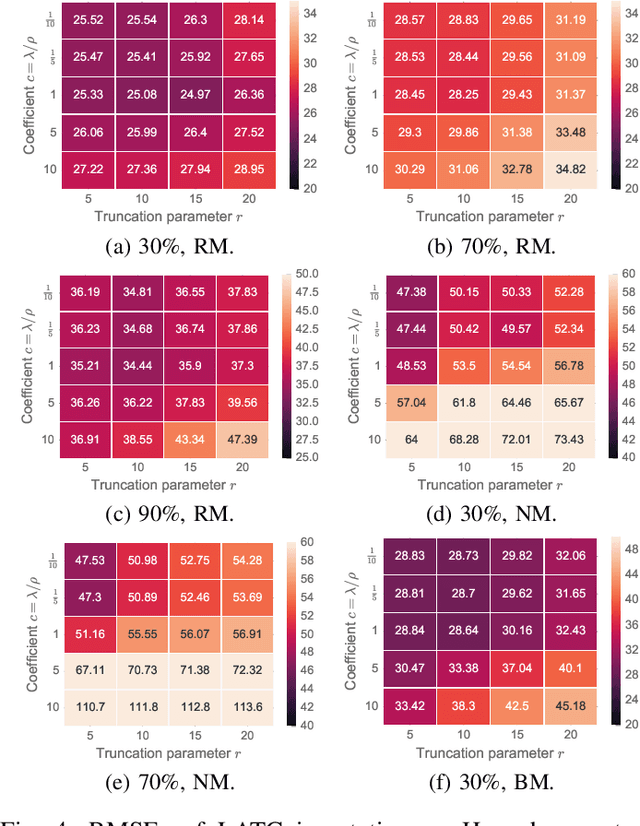
Spatiotemporal traffic time series (e.g., traffic volume/speed) collected from sensing systems are often incomplete with considerable corruption and large amounts of missing values, preventing users from harnessing the full power of the data. Missing data imputation has been a long-standing research topic and critical application for real-world intelligent transportation systems. A widely applied imputation method is low-rank matrix/tensor completion; however, the low-rank assumption only preserves the global structure while ignores the strong local consistency in spatiotemporal data. In this paper, we propose a low-rank autoregressive tensor completion (LATC) framework by introducing \textit{temporal variation} as a new regularization term into the completion of a third-order (sensor $\times$ time of day $\times$ day) tensor. The third-order tensor structure allows us to better capture the global consistency of traffic data, such as the inherent seasonality and day-to-day similarity. To achieve local consistency, we design the temporal variation by imposing an AR($p$) model for each time series with coefficients as learnable parameters. Different from previous spatial and temporal regularization schemes, the minimization of temporal variation can better characterize temporal generative mechanisms beyond local smoothness, allowing us to deal with more challenging scenarios such "blackout" missing. To solve the optimization problem in LATC, we introduce an alternating minimization scheme that estimates the low-rank tensor and autoregressive coefficients iteratively. We conduct extensive numerical experiments on several real-world traffic data sets, and our results demonstrate the effectiveness of LATC in diverse missing scenarios.

Boosted Convolutional Neural Networks for Motor Imagery EEG Decoding with Multiwavelet-based Time-Frequency Conditional Granger Causality Analysis

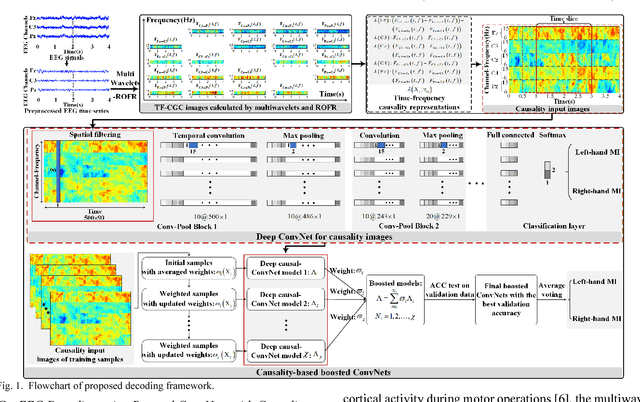
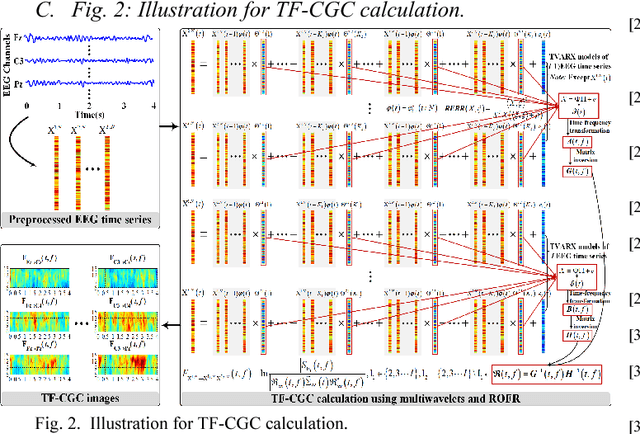
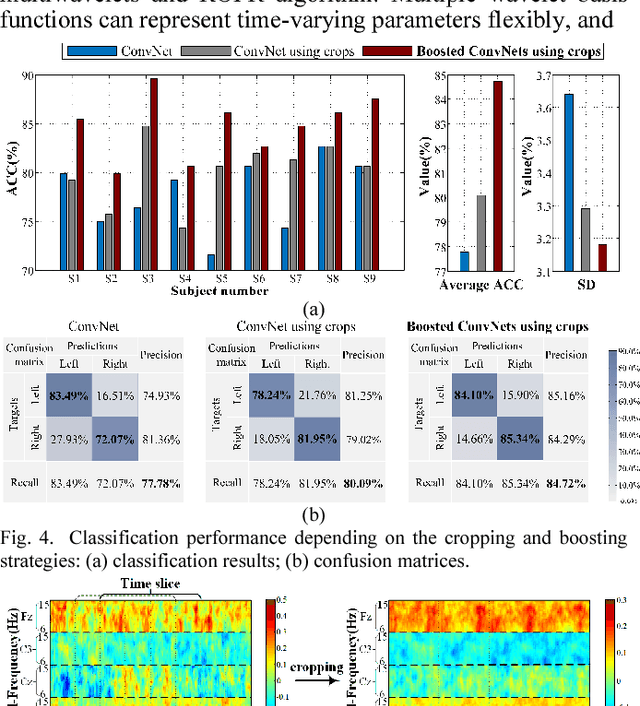
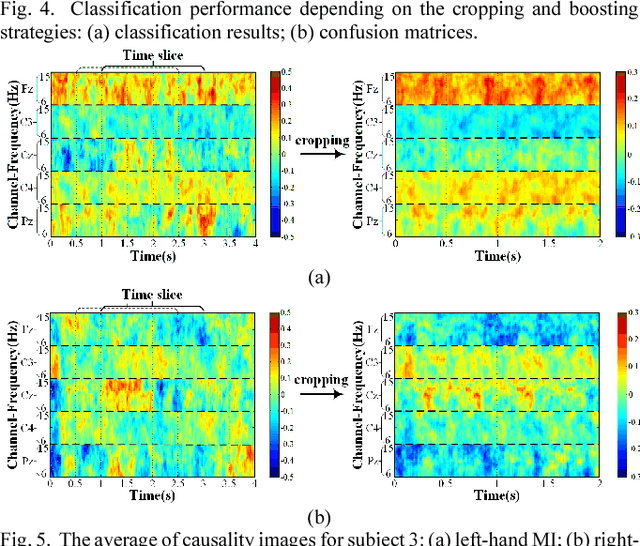
Decoding EEG signals of different mental states is a challenging task for brain-computer interfaces (BCIs) due to nonstationarity of perceptual decision processes. This paper presents a novel boosted convolutional neural networks (ConvNets) decoding scheme for motor imagery (MI) EEG signals assisted by the multiwavelet-based time-frequency (TF) causality analysis. Specifically, multiwavelet basis functions are first combined with Geweke spectral measure to obtain high-resolution TF-conditional Granger causality (CGC) representations, where a regularized orthogonal forward regression (ROFR) algorithm is adopted to detect a parsimonious model with good generalization performance. The causality images for network input preserving time, frequency and location information of connectivity are then designed based on the TF-CGC distributions of alpha band multichannel EEG signals. Further constructed boosted ConvNets by using spatio-temporal convolutions as well as advances in deep learning including cropping and boosting methods, to extract discriminative causality features and classify MI tasks. Our proposed approach outperforms the competition winner algorithm with 12.15% increase in average accuracy and 74.02% decrease in associated inter subject standard deviation for the same binary classification on BCI competition-IV dataset-IIa. Experiment results indicate that the boosted ConvNets with causality images works well in decoding MI-EEG signals and provides a promising framework for developing MI-BCI systems.