Covariance regression with random forests

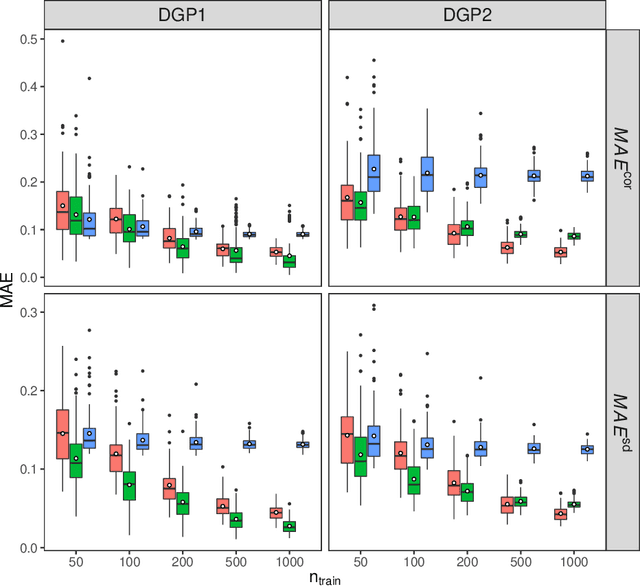
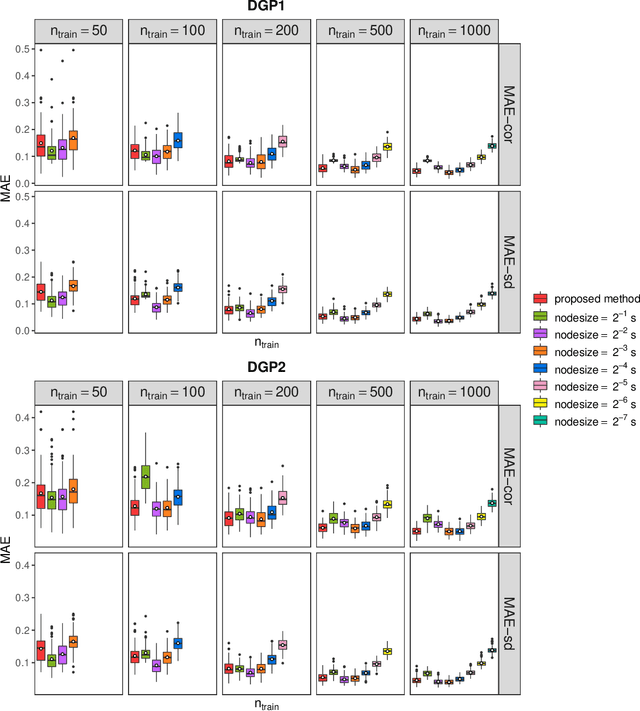
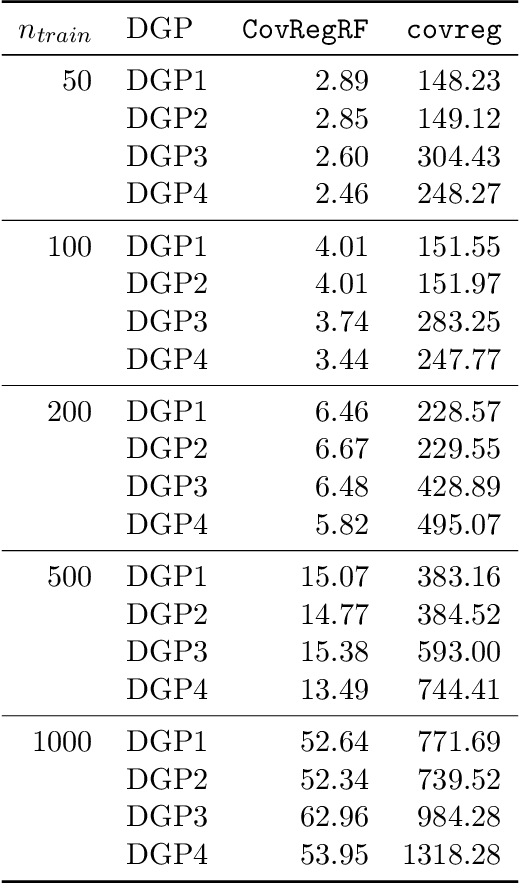
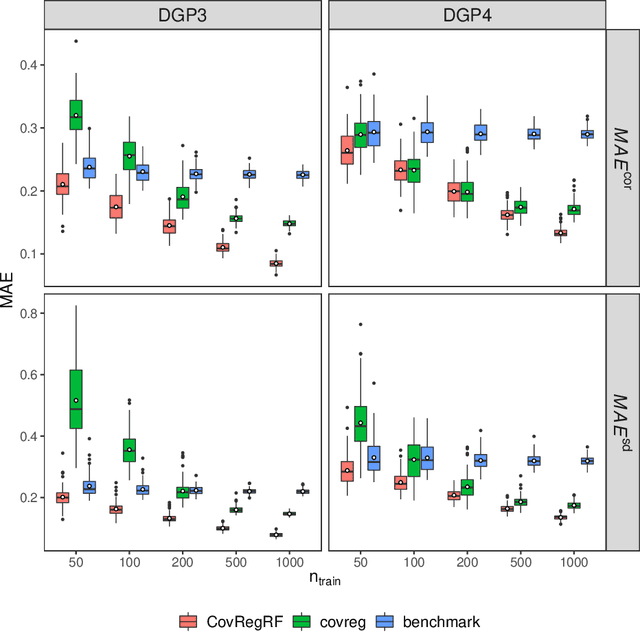
Capturing the conditional covariances or correlations among the elements of a multivariate response vector based on covariates is important to various fields including neuroscience, epidemiology and biomedicine. We propose a new method called Covariance Regression with Random Forests (CovRegRF) to estimate the covariance matrix of a multivariate response given a set of covariates, using a random forest framework. Random forest trees are built with a splitting rule specially designed to maximize the difference between the sample covariance matrix estimates of the child nodes. We also propose a significance test for the partial effect of a subset of covariates. We evaluate the performance of the proposed method and significance test through a simulation study which shows that the proposed method provides accurate covariance matrix estimates and that the Type-1 error is well controlled. We also demonstrate an application of the proposed method with a thyroid disease data set.

Bayesian Complementary Kernelized Learning for Multidimensional Spatiotemporal Data

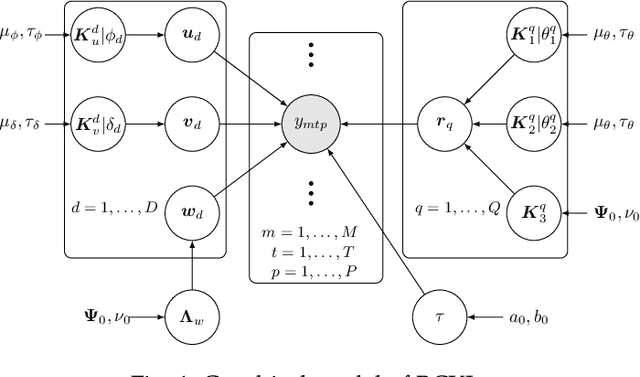
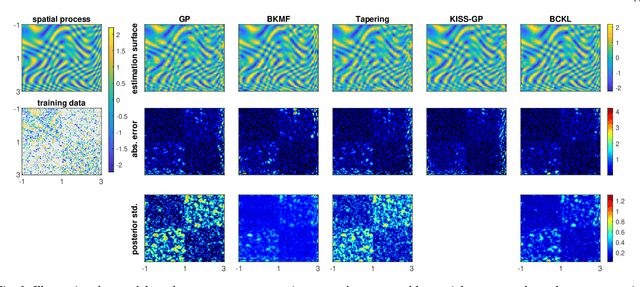
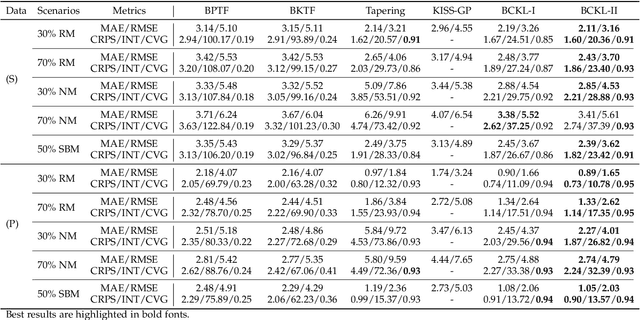
Probabilistic modeling of multidimensional spatiotemporal data is critical to many real-world applications. However, real-world spatiotemporal data often exhibits complex dependencies that are nonstationary, i.e., correlation structure varies with location/time, and nonseparable, i.e., dependencies exist between space and time. Developing effective and computationally efficient statistical models to accommodate nonstationary/nonseparable processes containing both long-range and short-scale variations becomes a challenging task, especially for large-scale datasets with various corruption/missing structures. In this paper, we propose a new statistical framework -- Bayesian Complementary Kernelized Learning (BCKL) -- to achieve scalable probabilistic modeling for multidimensional spatiotemporal data. To effectively describe complex dependencies, BCKL integrates kernelized low-rank factorization with short-range spatiotemporal Gaussian processes (GP), in which the two components complement each other. Specifically, we use a multi-linear low-rank factorization component to capture the global/long-range correlations in the data and introduce an additive short-scale GP based on compactly supported kernel functions to characterize the remaining local variabilities. We develop an efficient Markov chain Monte Carlo (MCMC) algorithm for model inference and evaluate the proposed BCKL framework on both synthetic and real-world spatiotemporal datasets. Our results confirm the superior performance of BCKL in providing accurate posterior mean and high-quality uncertainty estimates.

Spatial Aggregation and Temporal Convolution Networks for Real-time Kriging

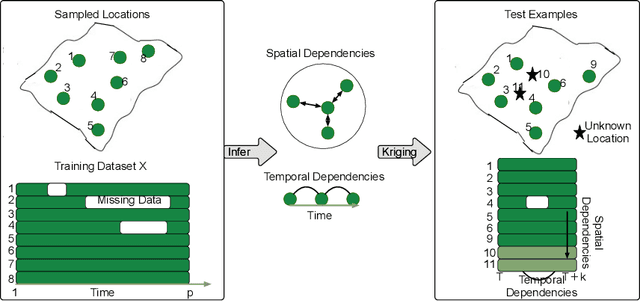
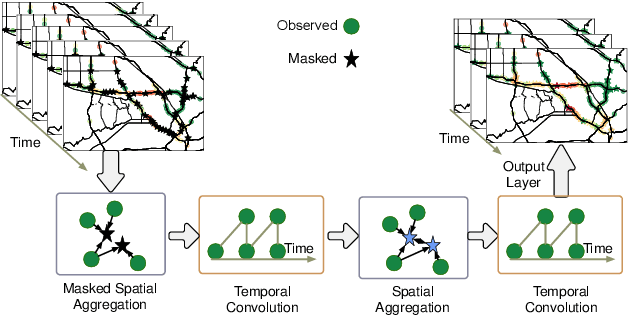
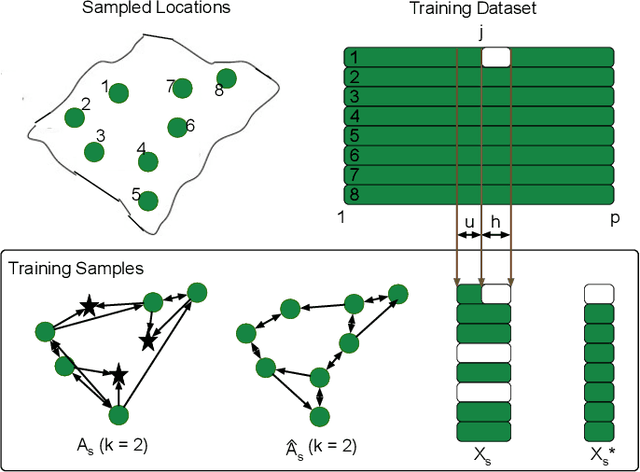
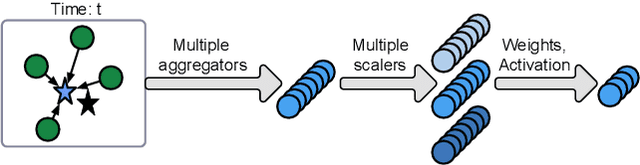
Spatiotemporal kriging is an important application in spatiotemporal data analysis, aiming to recover/interpolate signals for unsampled/unobserved locations based on observed signals. The principle challenge for spatiotemporal kriging is how to effectively model and leverage the spatiotemporal dependencies within the data. Recently, graph neural networks (GNNs) have shown great promise for spatiotemporal kriging tasks. However, standard GNNs often require a carefully designed adjacency matrix and specific aggregation functions, which are inflexible for general applications/problems. To address this issue, we present SATCN -- Spatial Aggregation and Temporal Convolution Networks -- a universal and flexible framework to perform spatiotemporal kriging for various spatiotemporal datasets without the need for model specification. Specifically, we propose a novel spatial aggregation network (SAN) inspired by Principal Neighborhood Aggregation, which uses multiple aggregation functions to help one node gather diverse information from its neighbors. To exclude information from unsampled nodes, a masking strategy that prevents the unsampled sensors from sending messages to their neighborhood is introduced to SAN. We capture temporal dependencies by the temporal convolutional networks, which allows our model to cope with data of diverse sizes. To make SATCN generalizable to unseen nodes and even unseen graph structures, we employ an inductive strategy to train SATCN. We conduct extensive experiments on three real-world spatiotemporal datasets, including traffic speed and climate recordings. Our results demonstrate the superiority of SATCN over traditional and GNN-based kriging models.

Scalable Spatiotemporally Varying Coefficient Modeling with Bayesian Kernelized Tensor Regression

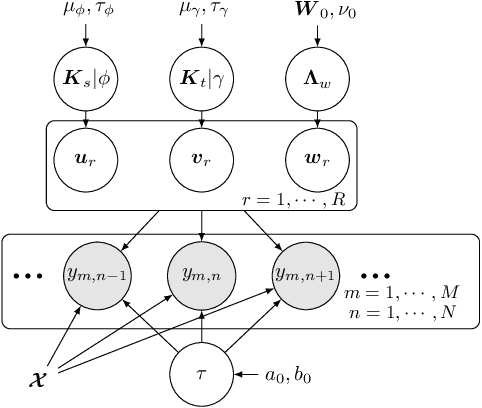
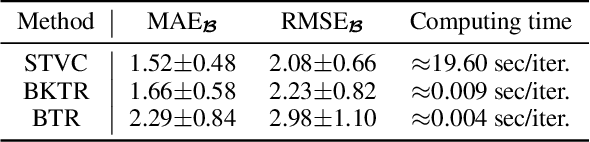
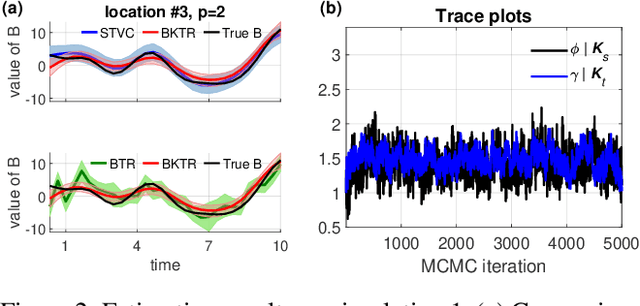
As a regression technique in spatial statistics, spatiotemporally varying coefficient model (STVC) is an important tool to discover nonstationary and interpretable response-covariate associations over both space and time. However, it is difficult to apply STVC for large-scale spatiotemporal analysis due to the high computational cost. To address this challenge, we summarize the spatiotemporally varying coefficients using a third-order tensor structure and propose to reformulate the spatiotemporally varying coefficient model as a special low-rank tensor regression problem. The low-rank decomposition can effectively model the global patterns of the large data with substantially reduced number of parameters. To further incorporate the local spatiotemporal dependencies among the samples, we place Gaussian process (GP) priors on the spatial and temporal factor matrices to better encode local spatial and temporal processes on each factor component. We refer to the overall framework as Bayesian Kernelized Tensor Regression (BKTR). For model inference, we develop an efficient Markov chain Monte Carlo (MCMC) algorithm, which uses Gibbs sampling to update factor matrices and slice sampling to update kernel hyperparameters. We conduct extensive experiments on both synthetic and real-world data sets, and our results confirm the superior performance and efficiency of BKTR for model estimation and parameter inference.

RFpredInterval: An R Package for Prediction Intervals with Random Forests and Boosted Forests

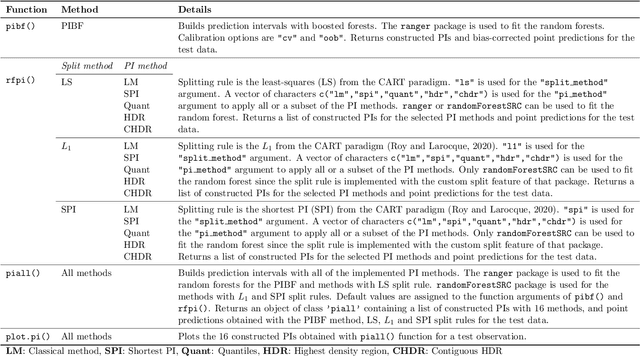
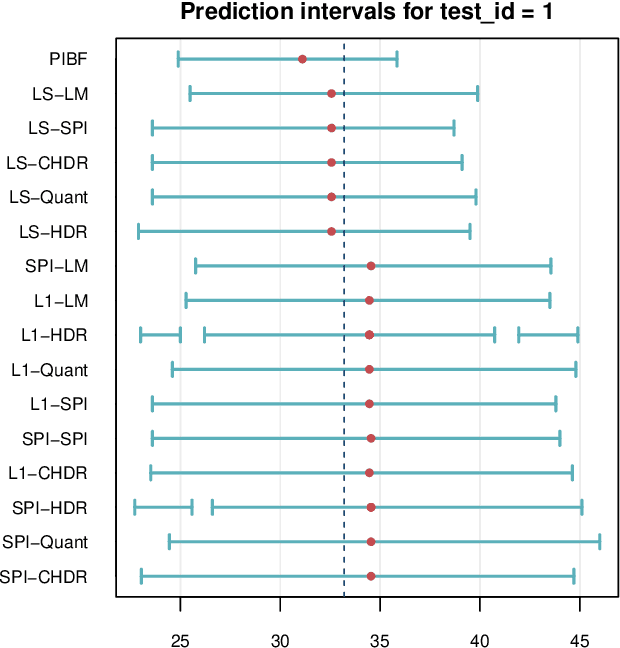
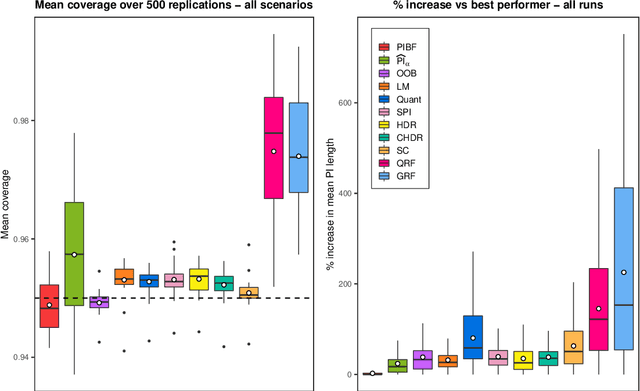
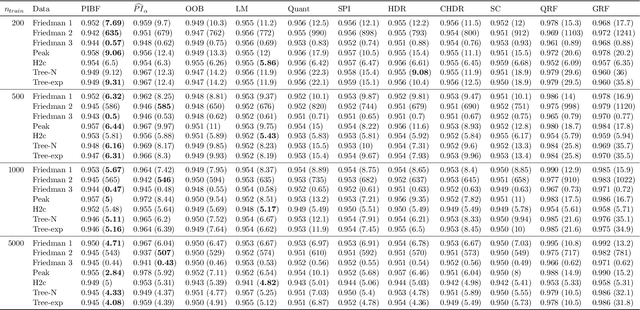
Like many predictive models, random forests provide a point prediction for a new observation. Besides the point prediction, it is important to quantify the uncertainty in the prediction. Prediction intervals provide information about the reliability of the point predictions. We have developed a comprehensive R package, RFpredInterval, that integrates 16 methods to build prediction intervals with random forests and boosted forests. The methods implemented in the package are a new method to build prediction intervals with boosted forests (PIBF) and 15 different variants to produce prediction intervals with random forests proposed by Roy and Larocque (2020). We perform an extensive simulation study and apply real data analyses to compare the performance of the proposed method to ten existing methods to build prediction intervals with random forests. The results show that the proposed method is very competitive and, globally, it outperforms the competing methods.

Conditional canonical correlation estimation based on covariates with random forests

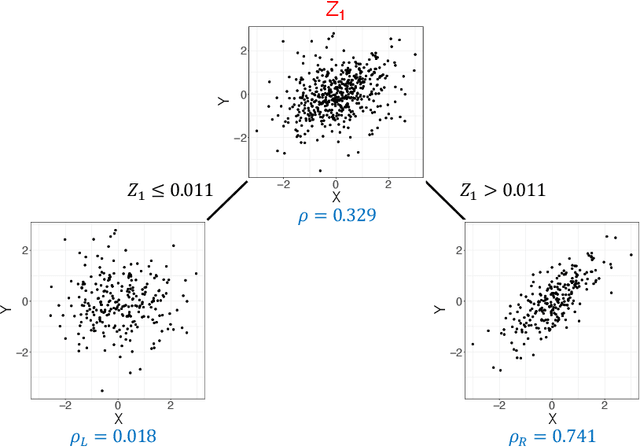
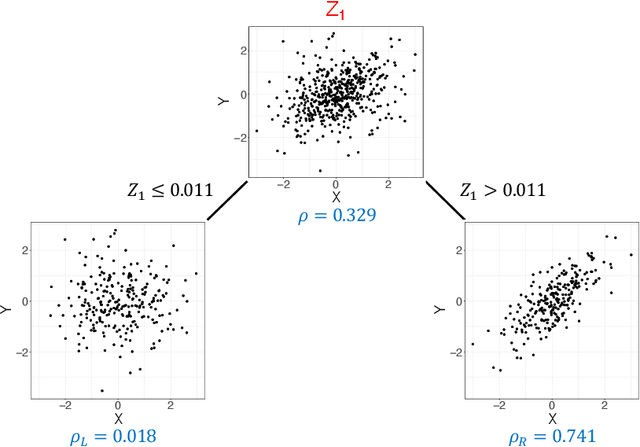
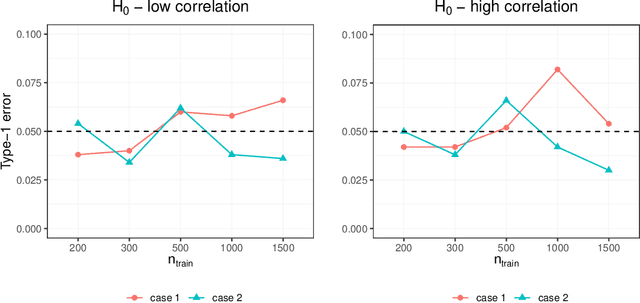
Investigating the relationships between two sets of variables helps to understand their interactions and can be done with canonical correlation analysis (CCA). However, the correlation between the two sets can sometimes depend on a third set of covariates, often subject-related ones such as age, gender, or other clinical measures. In this case, applying CCA to the whole population is not optimal and methods to estimate conditional CCA, given the covariates, can be useful. We propose a new method called Random Forest with Canonical Correlation Analysis (RFCCA) to estimate the conditional canonical correlations between two sets of variables given subject-related covariates. The individual trees in the forest are built with a splitting rule specifically designed to partition the data to maximize the canonical correlation heterogeneity between child nodes. We also propose a significance test to detect the global effect of the covariates on the relationship between two sets of variables. The performance of the proposed method and the global significance test is evaluated through simulation studies that show it provides accurate canonical correlation estimations and well-controlled Type-1 error. We also show an application of the proposed method with EEG data.

Inductive Graph Neural Networks for Spatiotemporal Kriging

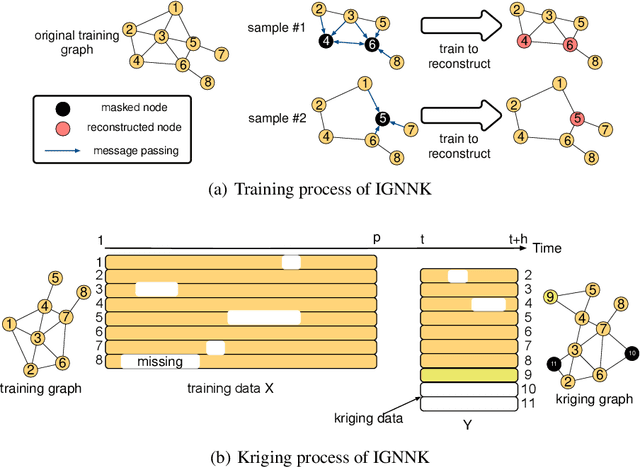
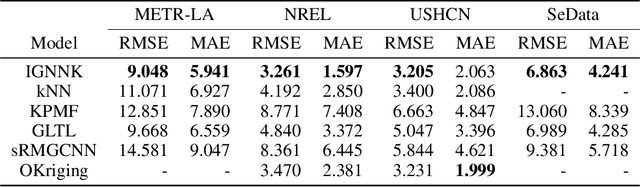
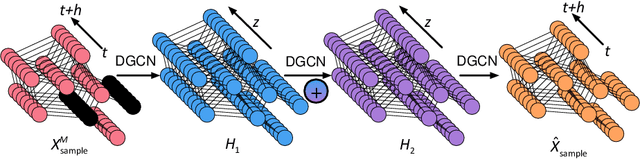
Time series forecasting and spatiotemporal kriging are the two most important tasks in spatiotemporal data analysis. Recent research on graph neural networks has made substantial progress in time series forecasting, while little attention is paid to the kriging problem---recovering signals for unsampled locations/sensors. Most existing scalable kriging methods (e.g., matrix/tensor completion) are transductive, and thus full retraining is required when we have a new sensor to interpolate. In this paper, we develop an Inductive Graph Neural Network Kriging (IGNNK) model to recover data for unsampled sensors on a network/graph structure. To generalize the effect of distance and reachability, we generate random subgraphs as samples and reconstruct the corresponding adjacency matrix for each sample. By reconstructing all signals on each sample subgraph, IGNNK can effectively learn the spatial message passing mechanism. Empirical results on several real-world spatiotemporal datasets demonstrate the effectiveness of our model. In addition, we also find that the learned model can be successfully transferred to the same type of kriging tasks on an unseen dataset. Our results show that: 1) GNN is an efficient and effective tool for spatial kriging; 2) inductive GNNs can be trained using dynamic adjacency matrices; and 3) a trained model can be transferred to new graph structures.