Improving the generalizability and robustness of large-scale traffic signal control

A number of deep reinforcement-learning (RL) approaches propose to control traffic signals. In this work, we study the robustness of such methods along two axes. First, sensor failures and GPS occlusions create missing-data challenges and we show that recent methods remain brittle in the face of these missing data. Second, we provide a more systematic study of the generalization ability of RL methods to new networks with different traffic regimes. Again, we identify the limitations of recent approaches. We then propose using a combination of distributional and vanilla reinforcement learning through a policy ensemble. Building upon the state-of-the-art previous model which uses a decentralized approach for large-scale traffic signal control with graph convolutional networks (GCNs), we first learn models using a distributional reinforcement learning (DisRL) approach. In particular, we use implicit quantile networks (IQN) to model the state-action return distribution with quantile regression. For traffic signal control problems, an ensemble of standard RL and DisRL yields superior performance across different scenarios, including different levels of missing sensor data and traffic flow patterns. Furthermore, the learning scheme of the resulting model can improve zero-shot transferability to different road network structures, including both synthetic networks and real-world networks (e.g., Luxembourg, Manhattan). We conduct extensive experiments to compare our approach to multi-agent reinforcement learning and traditional transportation approaches. Results show that the proposed method improves robustness and generalizability in the face of missing data, varying road networks, and traffic flows.

Covariance regression with random forests

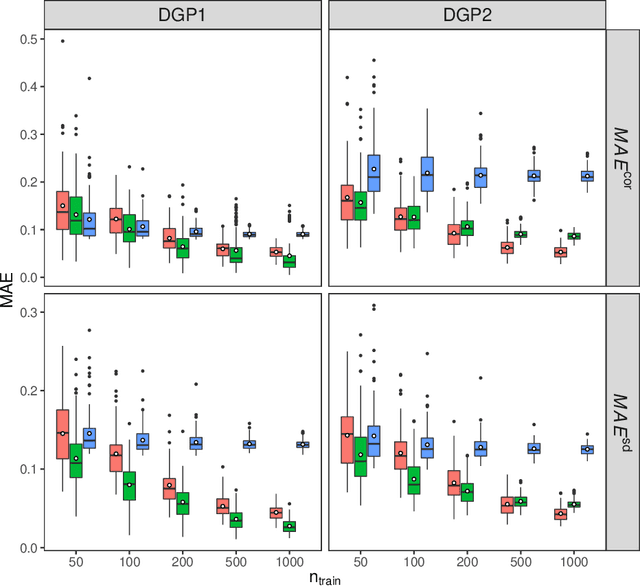
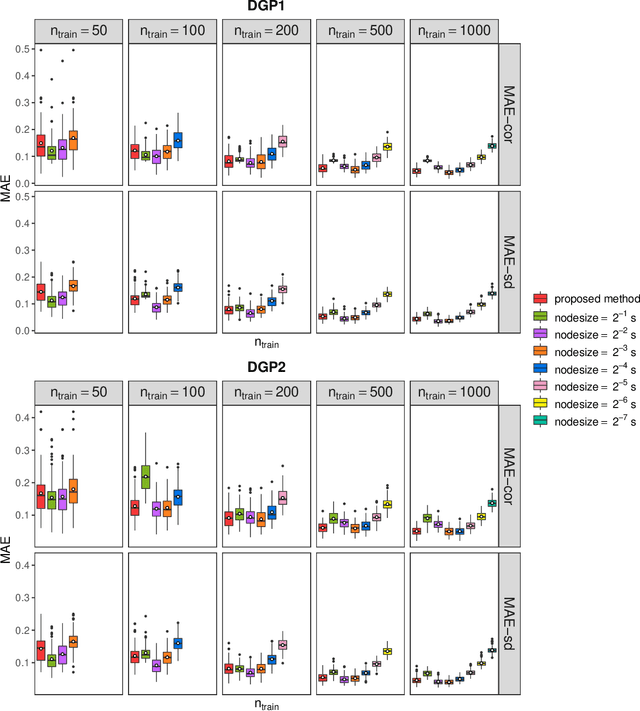
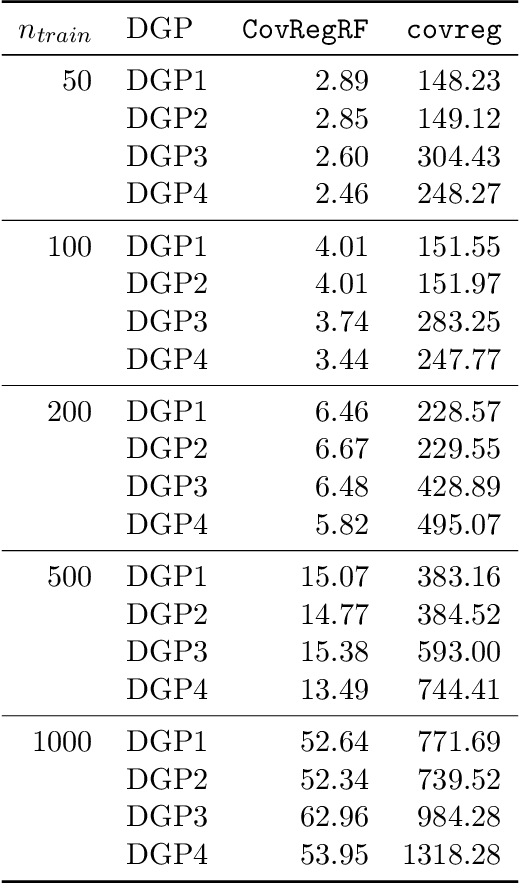
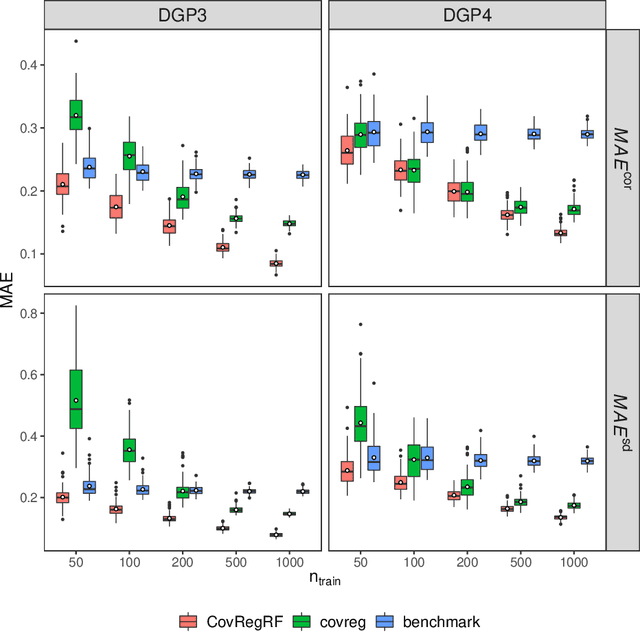
Capturing the conditional covariances or correlations among the elements of a multivariate response vector based on covariates is important to various fields including neuroscience, epidemiology and biomedicine. We propose a new method called Covariance Regression with Random Forests (CovRegRF) to estimate the covariance matrix of a multivariate response given a set of covariates, using a random forest framework. Random forest trees are built with a splitting rule specially designed to maximize the difference between the sample covariance matrix estimates of the child nodes. We also propose a significance test for the partial effect of a subset of covariates. We evaluate the performance of the proposed method and significance test through a simulation study which shows that the proposed method provides accurate covariance matrix estimates and that the Type-1 error is well controlled. We also demonstrate an application of the proposed method with a thyroid disease data set.

Model-based graph reinforcement learning for inductive traffic signal control

Most reinforcement learning methods for adaptive-traffic-signal-control require training from scratch to be applied on any new intersection or after any modification to the road network, traffic distribution, or behavioral constraints experienced during training. Considering 1) the massive amount of experience required to train such methods, and 2) that experience must be gathered by interacting in an exploratory fashion with real road-network-users, such a lack of transferability limits experimentation and applicability. Recent approaches enable learning policies that generalize for unseen road-network topologies and traffic distributions, partially tackling this challenge. However, the literature remains divided between the learning of cyclic (the evolution of connectivity at an intersection must respect a cycle) and acyclic (less constrained) policies, and these transferable methods 1) are only compatible with cyclic constraints and 2) do not enable coordination. We introduce a new model-based method, MuJAM, which, on top of enabling explicit coordination at scale for the first time, pushes generalization further by allowing a generalization to the controllers' constraints. In a zero-shot transfer setting involving both road networks and traffic settings never experienced during training, and in a larger transfer experiment involving the control of 3,971 traffic signal controllers in Manhattan, we show that MuJAM, using both cyclic and acyclic constraints, outperforms domain-specific baselines as well as another transferable approach.

RFpredInterval: An R Package for Prediction Intervals with Random Forests and Boosted Forests

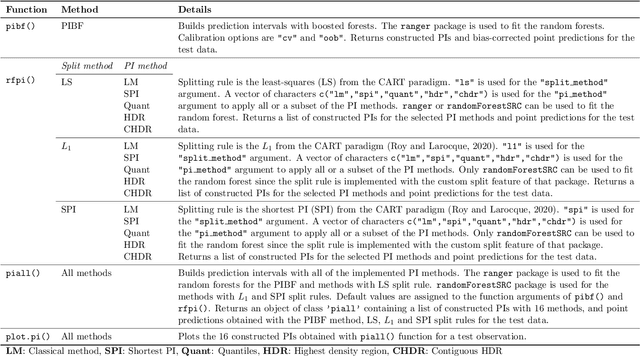
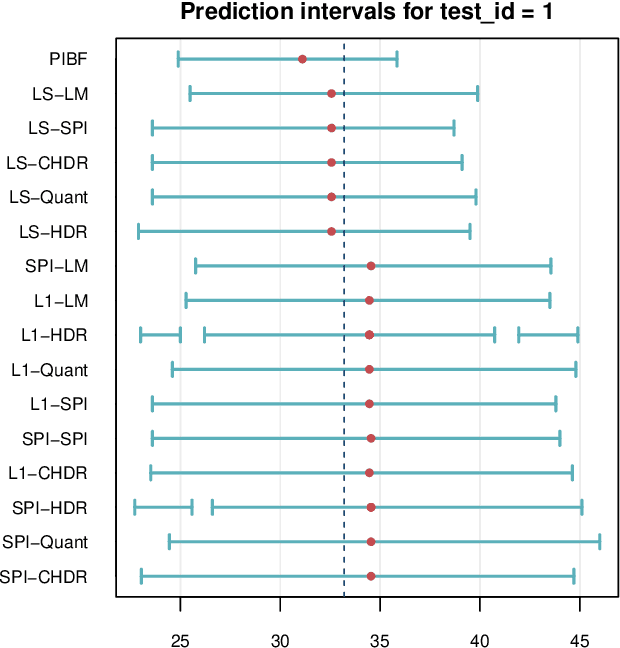
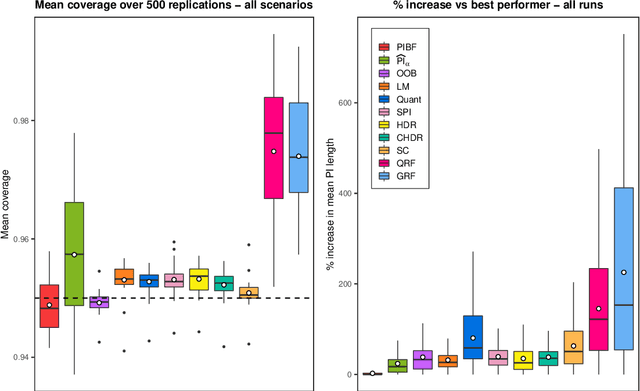
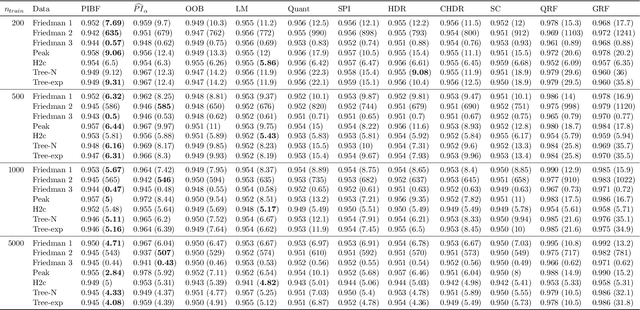
Like many predictive models, random forests provide a point prediction for a new observation. Besides the point prediction, it is important to quantify the uncertainty in the prediction. Prediction intervals provide information about the reliability of the point predictions. We have developed a comprehensive R package, RFpredInterval, that integrates 16 methods to build prediction intervals with random forests and boosted forests. The methods implemented in the package are a new method to build prediction intervals with boosted forests (PIBF) and 15 different variants to produce prediction intervals with random forests proposed by Roy and Larocque (2020). We perform an extensive simulation study and apply real data analyses to compare the performance of the proposed method to ten existing methods to build prediction intervals with random forests. The results show that the proposed method is very competitive and, globally, it outperforms the competing methods.

Conditional canonical correlation estimation based on covariates with random forests

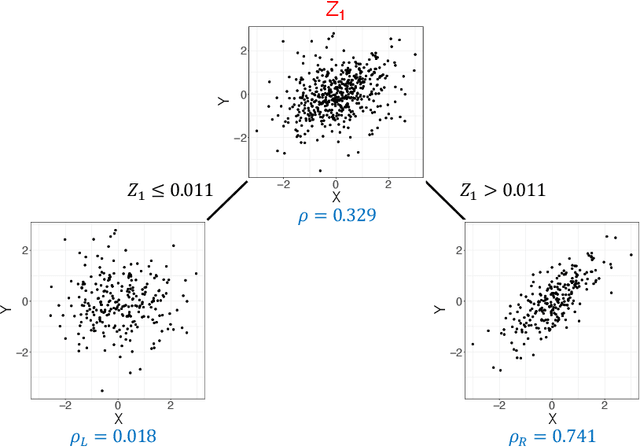
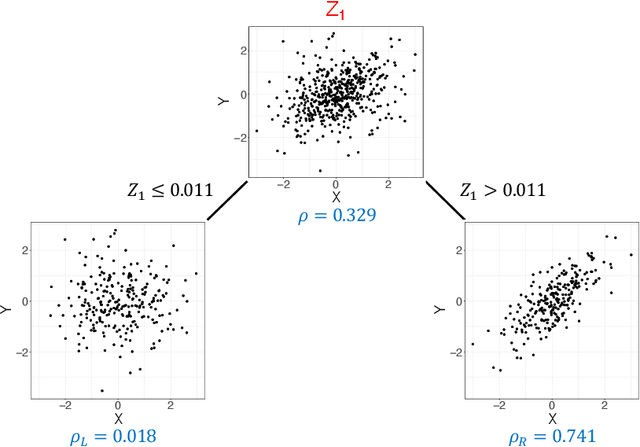
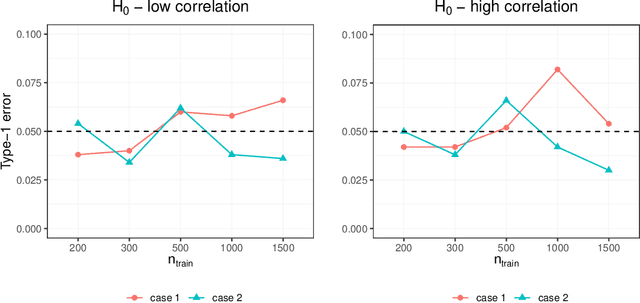
Investigating the relationships between two sets of variables helps to understand their interactions and can be done with canonical correlation analysis (CCA). However, the correlation between the two sets can sometimes depend on a third set of covariates, often subject-related ones such as age, gender, or other clinical measures. In this case, applying CCA to the whole population is not optimal and methods to estimate conditional CCA, given the covariates, can be useful. We propose a new method called Random Forest with Canonical Correlation Analysis (RFCCA) to estimate the conditional canonical correlations between two sets of variables given subject-related covariates. The individual trees in the forest are built with a splitting rule specifically designed to partition the data to maximize the canonical correlation heterogeneity between child nodes. We also propose a significance test to detect the global effect of the covariates on the relationship between two sets of variables. The performance of the proposed method and the global significance test is evaluated through simulation studies that show it provides accurate canonical correlation estimations and well-controlled Type-1 error. We also show an application of the proposed method with EEG data.

Ensemble Methods for Survival Data with Time-Varying Covariates

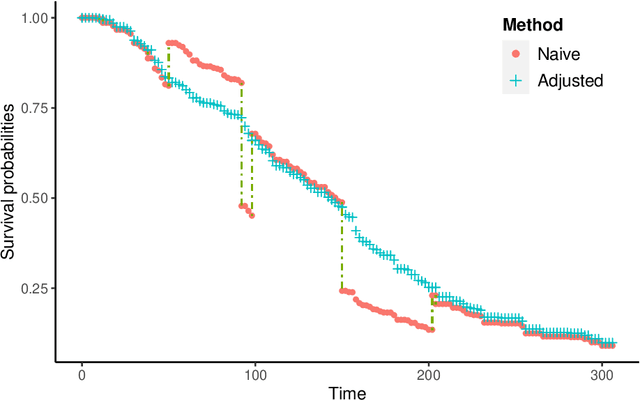
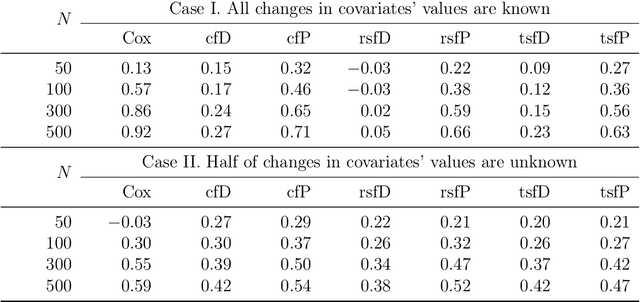
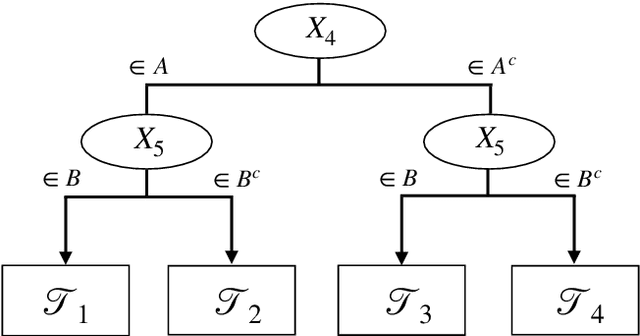
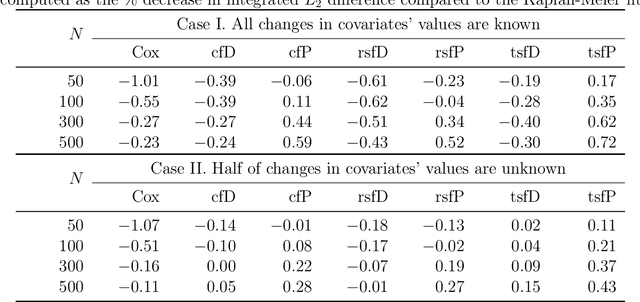
We propose two new survival forests for survival data with time-varying covariates. They are generalizations of random survival forest and conditional inference forest -- the traditional survival forests for right-censored data with time-invariant covariates. We investigate the properties of these new forests, as well as that of the recently-proposed transformation forest, and compare their performances with that of the Cox model via a comprehensive simulation study. In particular, the simulations compare the performance of the forests when all changes in the covariates' values are known with the case when not all changes are known. We also study the forests under the proportional hazards setting as well as the non-proportional hazards setting, where the forests based on log-rank splitting tend to perform worse than does the transformation forest. We then provide guidance for choosing among the modeling methods. Finally, we show that the performance of the survival forests for time-invariant covariate data is broadly similar to that found for time-varying covariate data.

IG-RL: Inductive Graph Reinforcement Learning for Massive-Scale Traffic Signal Control

Scaling adaptive traffic-signal control involves dealing with combinatorial state and action spaces. Multi-agent reinforcement learning attempts to address this challenge by distributing control to specialized agents. However, specialization hinders generalization and transferability, and the computational graphs underlying neural-networks architectures---dominating in the multi-agent setting---do not offer the flexibility to handle an arbitrary number of entities which changes both between road networks, and over time as vehicles traverse the network. We introduce Inductive Graph Reinforcement Learning (IG-RL) based on graph-convolutional networks which adapts to the structure of any road network, to learn detailed representations of traffic-controllers and their surroundings. Our decentralized approach enables learning of a transferable-adaptive-traffic-signal-control policy. After being trained on an arbitrary set of road networks, our model can generalize to new road networks, traffic distributions, and traffic regimes, with no additional training and a constant number of parameters, enabling greater scalability compared to prior methods. Furthermore, our approach can exploit the granularity of available data by capturing the (dynamic) demand at both the lane and the vehicle levels. The proposed method is tested on both road networks and traffic settings never experienced during training. We compare IG-RL to multi-agent reinforcement learning and domain-specific baselines. In both synthetic road networks and in a larger experiment involving the control of the 3,971 traffic signals of Manhattan, we show that different instantiations of IG-RL outperform baselines.