Ensemble Methods for Survival Data with Time-Varying Covariates

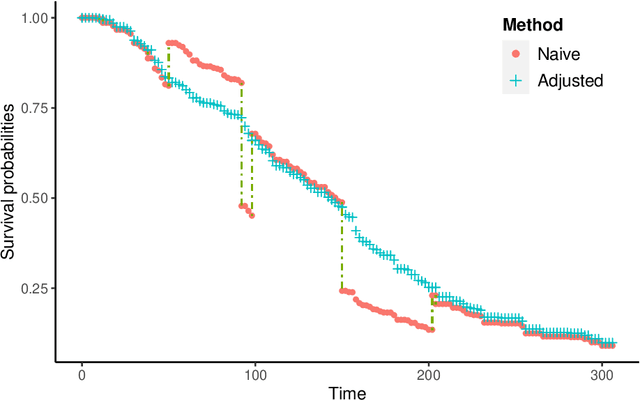
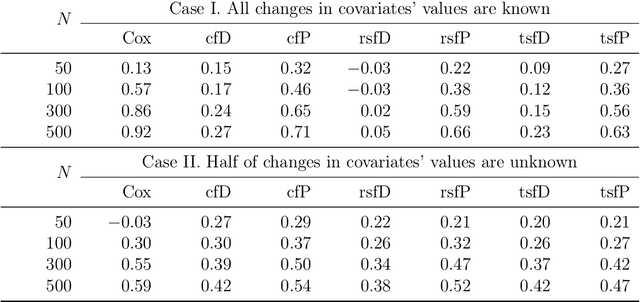
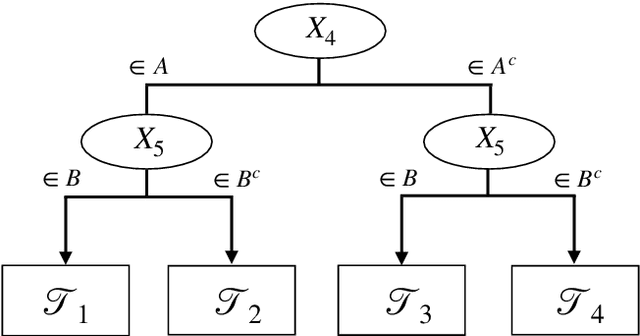
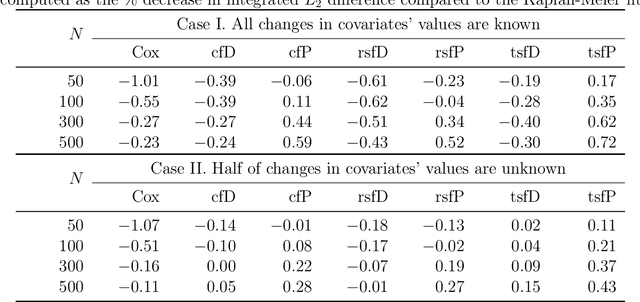
We propose two new survival forests for survival data with time-varying covariates. They are generalizations of random survival forest and conditional inference forest -- the traditional survival forests for right-censored data with time-invariant covariates. We investigate the properties of these new forests, as well as that of the recently-proposed transformation forest, and compare their performances with that of the Cox model via a comprehensive simulation study. In particular, the simulations compare the performance of the forests when all changes in the covariates' values are known with the case when not all changes are known. We also study the forests under the proportional hazards setting as well as the non-proportional hazards setting, where the forests based on log-rank splitting tend to perform worse than does the transformation forest. We then provide guidance for choosing among the modeling methods. Finally, we show that the performance of the survival forests for time-invariant covariate data is broadly similar to that found for time-varying covariate data.