The passive symmetries of machine learning

Any representation of data involves arbitrary investigator choices. Because those choices are external to the data-generating process, each choice leads to an exact symmetry, corresponding to the group of transformations that takes one possible representation to another. These are the passive symmetries; they include coordinate freedom, gauge symmetry and units covariance, all of which have led to important results in physics. Our goal is to understand the implications of passive symmetries for machine learning: Which passive symmetries play a role (e.g., permutation symmetry in graph neural networks)? What are dos and don'ts in machine learning practice? We assay conditions under which passive symmetries can be implemented as group equivariances. We also discuss links to causal modeling, and argue that the implementation of passive symmetries is particularly valuable when the goal of the learning problem is to generalize out of sample. While this paper is purely conceptual, we believe that it can have a significant impact on helping machine learning make the transition that took place for modern physics in the first half of the Twentieth century.

Dimensionless machine learning: Imposing exact units equivariance

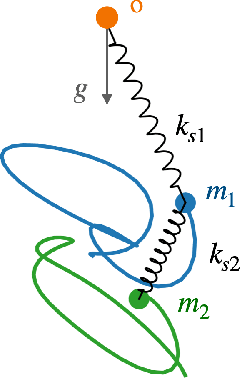
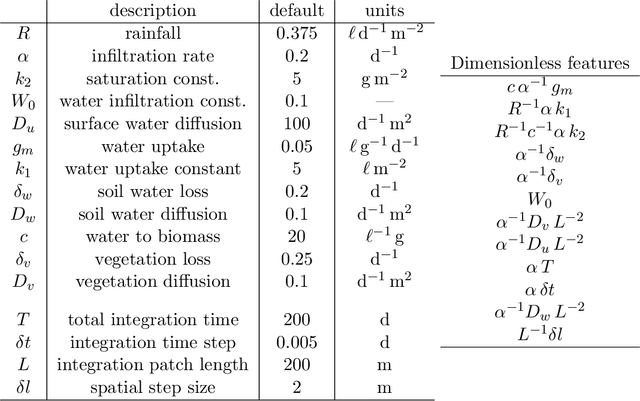
Units equivariance is the exact symmetry that follows from the requirement that relationships among measured quantities of physics relevance must obey self-consistent dimensional scalings. Here, we employ dimensional analysis and ideas from equivariant machine learning to provide a two stage learning procedure for units-equivariant machine learning. For a given learning task, we first construct a dimensionless version of its inputs using classic results from dimensional analysis, and then perform inference in the dimensionless space. Our approach can be used to impose units equivariance across a broad range of machine learning methods which are equivariant to rotations and other groups. We discuss the in-sample and out-of-sample prediction accuracy gains one can obtain in contexts like symbolic regression and emulation, where symmetry is important. We illustrate our approach with simple numerical examples involving dynamical systems in physics and ecology.

A simple equivariant machine learning method for dynamics based on scalars

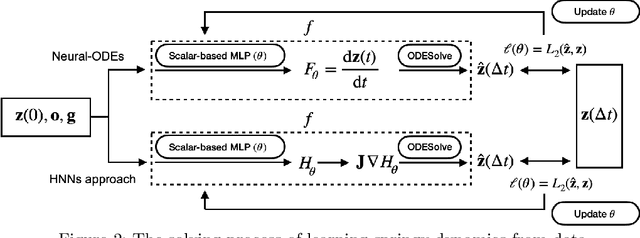
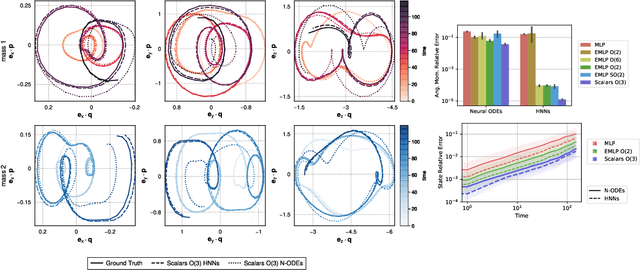
Physical systems obey strict symmetry principles. We expect that machine learning methods that intrinsically respect these symmetries should have higher prediction accuracy and better generalization in prediction of physical dynamics. In this work we implement a principled model based on invariant scalars, and release open-source code. We apply this Scalars method to a simple chaotic dynamical system, the springy double pendulum. We show that the Scalars method outperforms state-of-the-art approaches for learning the properties of physical systems with symmetries, both in terms of accuracy and speed. Because the method incorporates the fundamental symmetries, we expect it to generalize to different settings, such as changes in the force laws in the system.

Scalars are universal: Gauge-equivariant machine learning, structured like classical physics

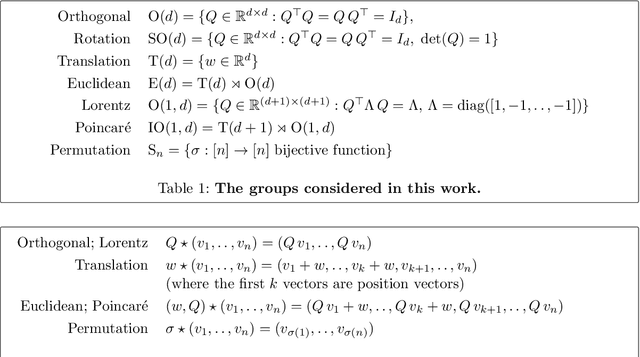
There has been enormous progress in the last few years in designing conceivable (though not always practical) neural networks that respect the gauge symmetries -- or coordinate freedom -- of physical law. Some of these frameworks make use of irreducible representations, some make use of higher order tensor objects, and some apply symmetry-enforcing constraints. Different physical laws obey different combinations of fundamental symmetries, but a large fraction (possibly all) of classical physics is equivariant to translation, rotation, reflection (parity), boost (relativity), and permutations. Here we show that it is simple to parameterize universally approximating polynomial functions that are equivariant under these symmetries, or under the Euclidean, Lorentz, and Poincar\'e groups, at any dimensionality $d$. The key observation is that nonlinear O($d$)-equivariant (and related-group-equivariant) functions can be expressed in terms of a lightweight collection of scalars -- scalar products and scalar contractions of the scalar, vector, and tensor inputs. These results demonstrate theoretically that gauge-invariant deep learning models for classical physics with good scaling for large problems are feasible right now.

Ensemble Methods for Survival Data with Time-Varying Covariates

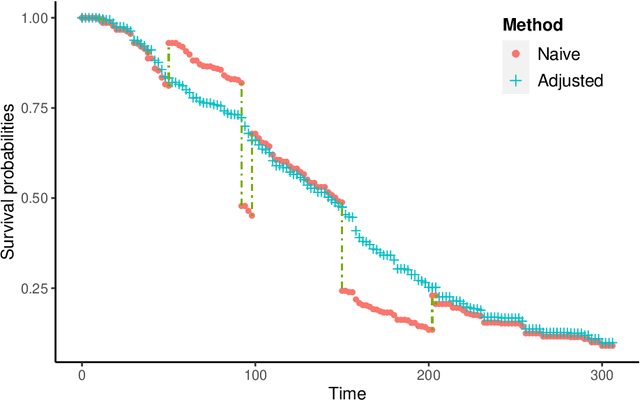
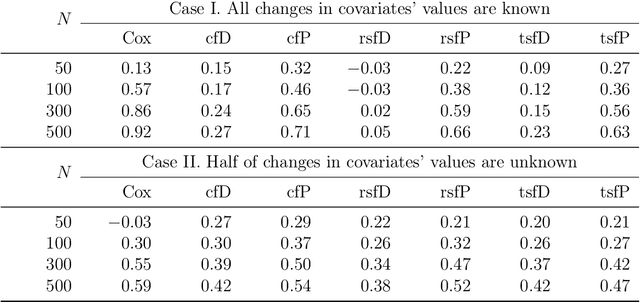
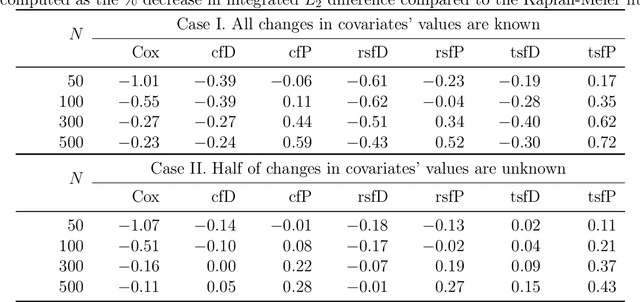
We propose two new survival forests for survival data with time-varying covariates. They are generalizations of random survival forest and conditional inference forest -- the traditional survival forests for right-censored data with time-invariant covariates. We investigate the properties of these new forests, as well as that of the recently-proposed transformation forest, and compare their performances with that of the Cox model via a comprehensive simulation study. In particular, the simulations compare the performance of the forests when all changes in the covariates' values are known with the case when not all changes are known. We also study the forests under the proportional hazards setting as well as the non-proportional hazards setting, where the forests based on log-rank splitting tend to perform worse than does the transformation forest. We then provide guidance for choosing among the modeling methods. Finally, we show that the performance of the survival forests for time-invariant covariate data is broadly similar to that found for time-varying covariate data.

Experimental performance of graph neural networks on random instances of max-cut

This note explores the applicability of unsupervised machine learning techniques towards hard optimization problems on random inputs. In particular we consider Graph Neural Networks (GNNs) -- a class of neural networks designed to learn functions on graphs -- and we apply them to the max-cut problem on random regular graphs. We focus on the max-cut problem on random regular graphs because it is a fundamental problem that has been widely studied. In particular, even though there is no known explicit solution to compare the output of our algorithm to, we can leverage the known asymptotics of the optimal max-cut value in order to evaluate the performance of the GNNs. In order to put the performance of the GNNs in context, we compare it with the classical semidefinite relaxation approach by Goemans and Williamson~(SDP), and with extremal optimization, which is a local optimization heuristic from the statistical physics literature. The numerical results we obtain indicate that, surprisingly, Graph Neural Networks attain comparable performance to the Goemans and Williamson SDP. We also observe that extremal optimization consistently outperforms the other two methods. Furthermore, the performances of the three methods present similar patterns, that is, for sparser, and for larger graphs, the size of the found cuts are closer to the asymptotic optimal max-cut value.