A simple equivariant machine learning method for dynamics based on scalars

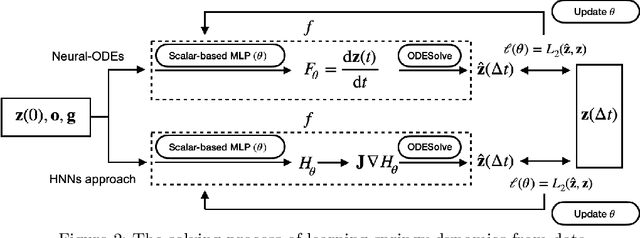
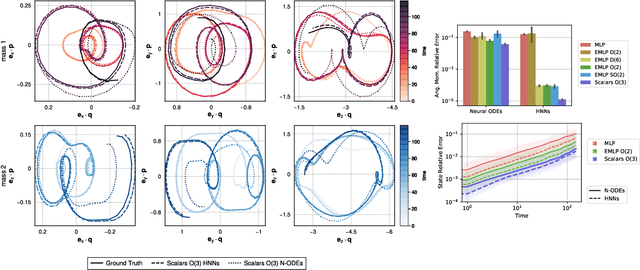
Physical systems obey strict symmetry principles. We expect that machine learning methods that intrinsically respect these symmetries should have higher prediction accuracy and better generalization in prediction of physical dynamics. In this work we implement a principled model based on invariant scalars, and release open-source code. We apply this Scalars method to a simple chaotic dynamical system, the springy double pendulum. We show that the Scalars method outperforms state-of-the-art approaches for learning the properties of physical systems with symmetries, both in terms of accuracy and speed. Because the method incorporates the fundamental symmetries, we expect it to generalize to different settings, such as changes in the force laws in the system.

Scalars are universal: Gauge-equivariant machine learning, structured like classical physics

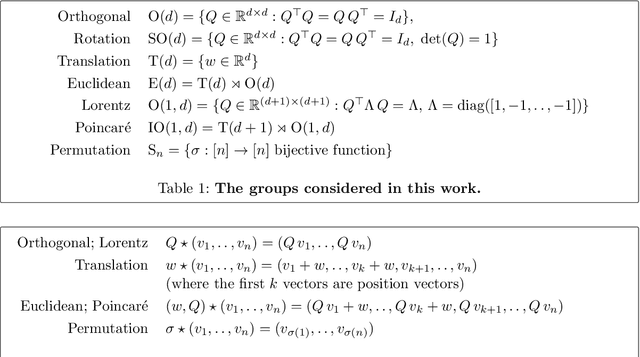
There has been enormous progress in the last few years in designing conceivable (though not always practical) neural networks that respect the gauge symmetries -- or coordinate freedom -- of physical law. Some of these frameworks make use of irreducible representations, some make use of higher order tensor objects, and some apply symmetry-enforcing constraints. Different physical laws obey different combinations of fundamental symmetries, but a large fraction (possibly all) of classical physics is equivariant to translation, rotation, reflection (parity), boost (relativity), and permutations. Here we show that it is simple to parameterize universally approximating polynomial functions that are equivariant under these symmetries, or under the Euclidean, Lorentz, and Poincar\'e groups, at any dimensionality $d$. The key observation is that nonlinear O($d$)-equivariant (and related-group-equivariant) functions can be expressed in terms of a lightweight collection of scalars -- scalar products and scalar contractions of the scalar, vector, and tensor inputs. These results demonstrate theoretically that gauge-invariant deep learning models for classical physics with good scaling for large problems are feasible right now.