A simple equivariant machine learning method for dynamics based on scalars
Paper and Code
Oct 30, 2021
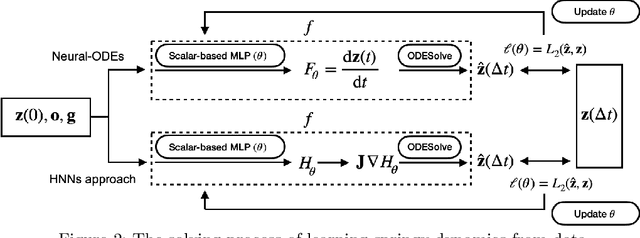
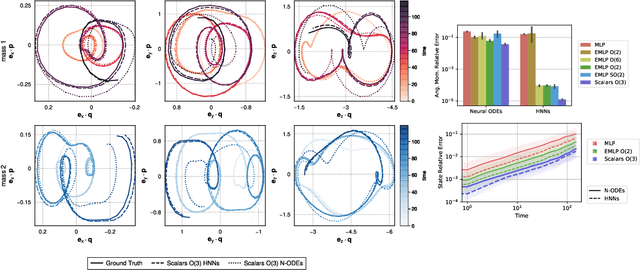
Physical systems obey strict symmetry principles. We expect that machine learning methods that intrinsically respect these symmetries should have higher prediction accuracy and better generalization in prediction of physical dynamics. In this work we implement a principled model based on invariant scalars, and release open-source code. We apply this Scalars method to a simple chaotic dynamical system, the springy double pendulum. We show that the Scalars method outperforms state-of-the-art approaches for learning the properties of physical systems with symmetries, both in terms of accuracy and speed. Because the method incorporates the fundamental symmetries, we expect it to generalize to different settings, such as changes in the force laws in the system.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge