Conditional canonical correlation estimation based on covariates with random forests

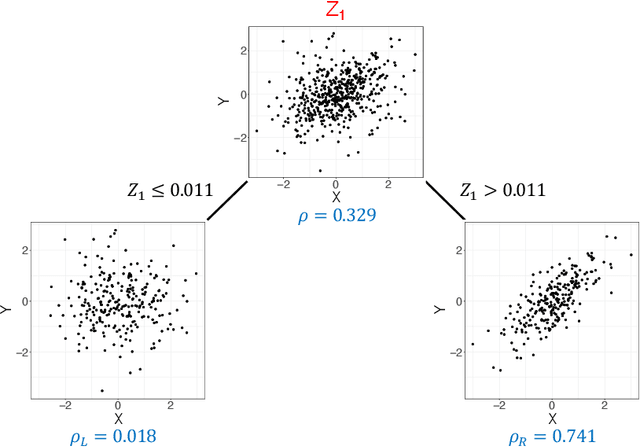
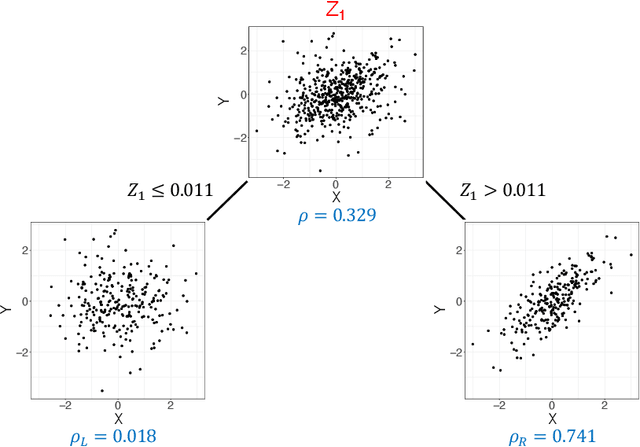
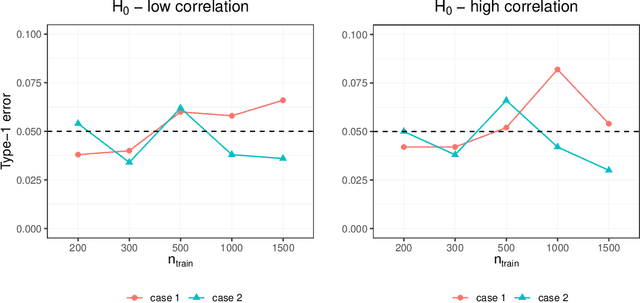
Investigating the relationships between two sets of variables helps to understand their interactions and can be done with canonical correlation analysis (CCA). However, the correlation between the two sets can sometimes depend on a third set of covariates, often subject-related ones such as age, gender, or other clinical measures. In this case, applying CCA to the whole population is not optimal and methods to estimate conditional CCA, given the covariates, can be useful. We propose a new method called Random Forest with Canonical Correlation Analysis (RFCCA) to estimate the conditional canonical correlations between two sets of variables given subject-related covariates. The individual trees in the forest are built with a splitting rule specifically designed to partition the data to maximize the canonical correlation heterogeneity between child nodes. We also propose a significance test to detect the global effect of the covariates on the relationship between two sets of variables. The performance of the proposed method and the global significance test is evaluated through simulation studies that show it provides accurate canonical correlation estimations and well-controlled Type-1 error. We also show an application of the proposed method with EEG data.