Covariance regression with random forests

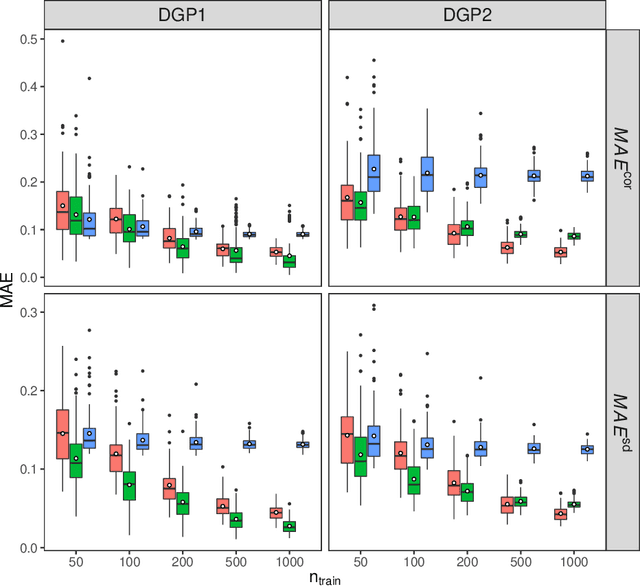
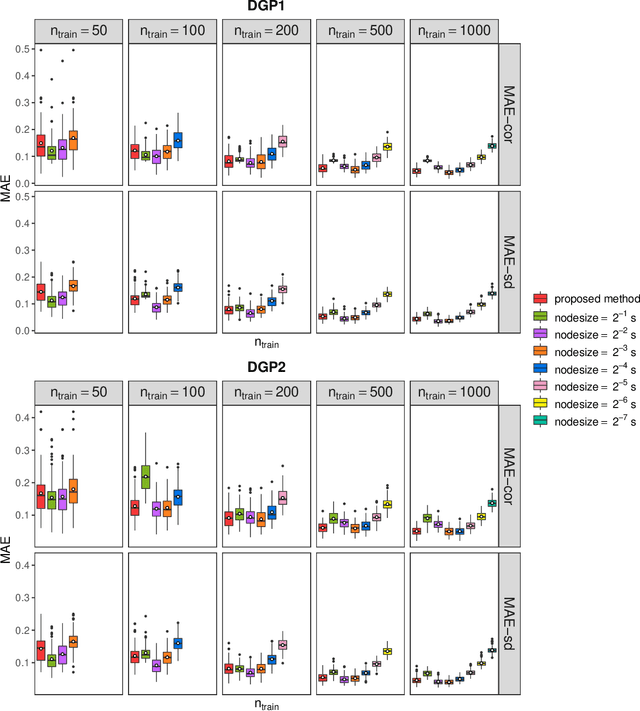
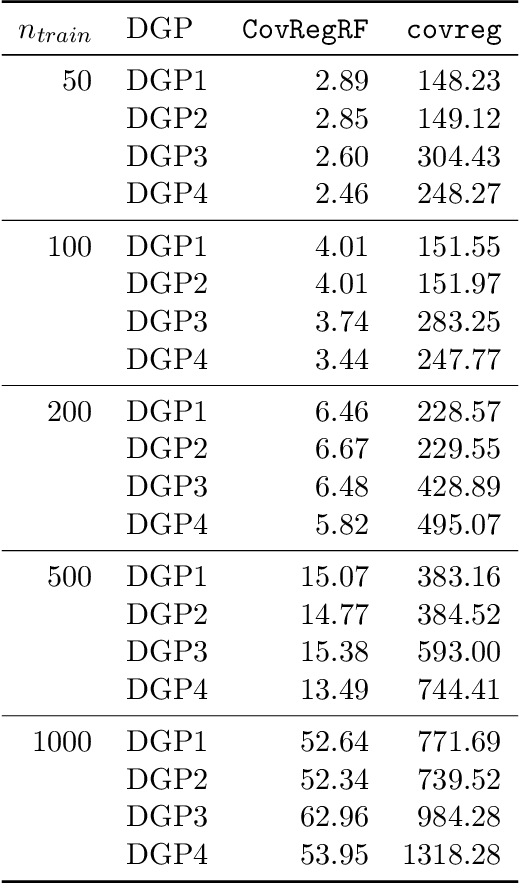
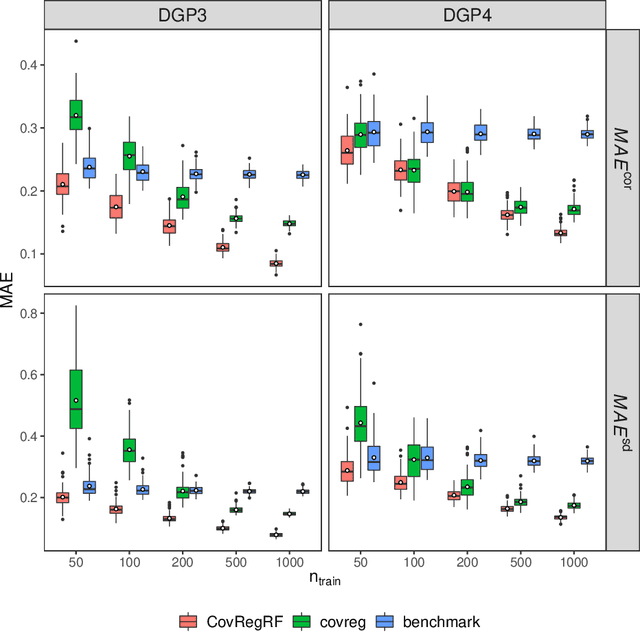
Capturing the conditional covariances or correlations among the elements of a multivariate response vector based on covariates is important to various fields including neuroscience, epidemiology and biomedicine. We propose a new method called Covariance Regression with Random Forests (CovRegRF) to estimate the covariance matrix of a multivariate response given a set of covariates, using a random forest framework. Random forest trees are built with a splitting rule specially designed to maximize the difference between the sample covariance matrix estimates of the child nodes. We also propose a significance test for the partial effect of a subset of covariates. We evaluate the performance of the proposed method and significance test through a simulation study which shows that the proposed method provides accurate covariance matrix estimates and that the Type-1 error is well controlled. We also demonstrate an application of the proposed method with a thyroid disease data set.

RFpredInterval: An R Package for Prediction Intervals with Random Forests and Boosted Forests

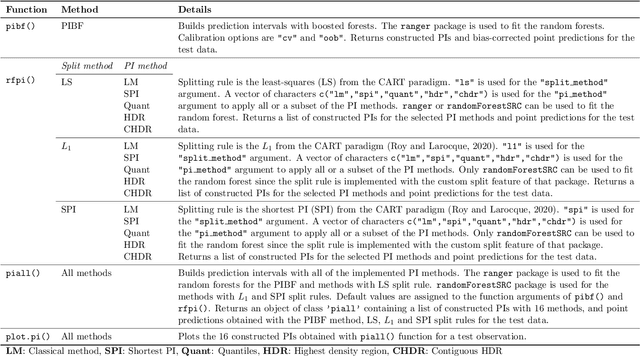
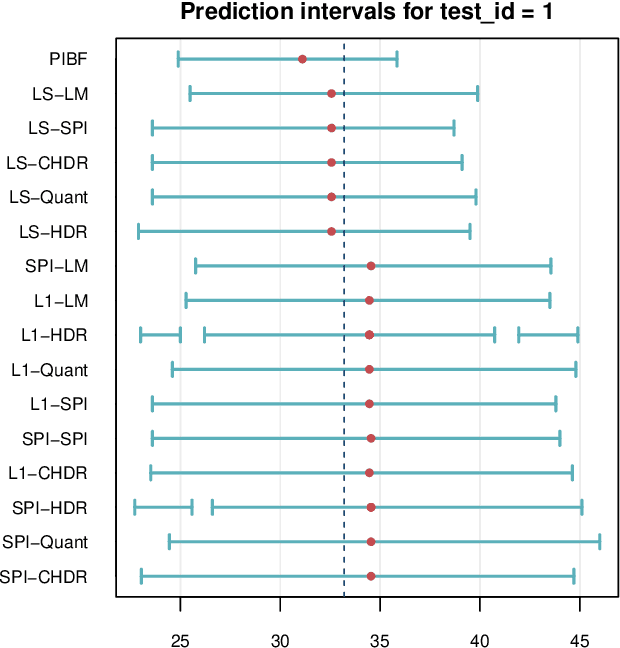
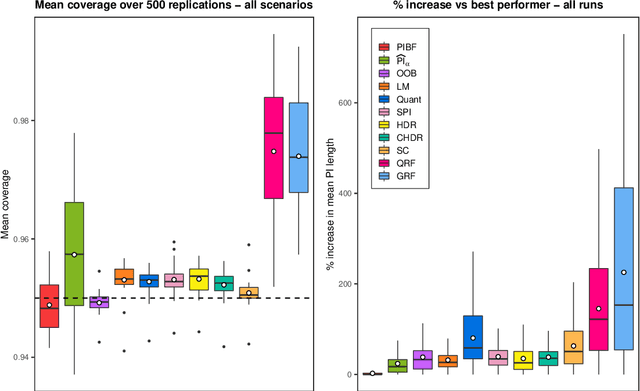
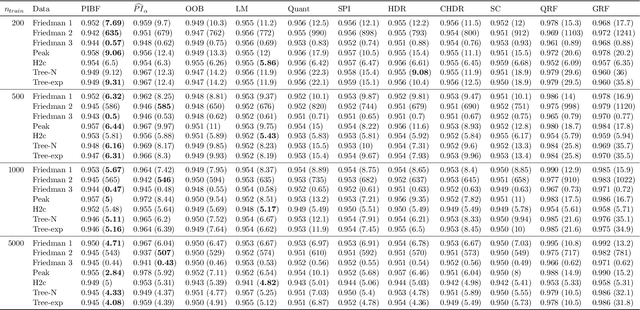
Like many predictive models, random forests provide a point prediction for a new observation. Besides the point prediction, it is important to quantify the uncertainty in the prediction. Prediction intervals provide information about the reliability of the point predictions. We have developed a comprehensive R package, RFpredInterval, that integrates 16 methods to build prediction intervals with random forests and boosted forests. The methods implemented in the package are a new method to build prediction intervals with boosted forests (PIBF) and 15 different variants to produce prediction intervals with random forests proposed by Roy and Larocque (2020). We perform an extensive simulation study and apply real data analyses to compare the performance of the proposed method to ten existing methods to build prediction intervals with random forests. The results show that the proposed method is very competitive and, globally, it outperforms the competing methods.

Conditional canonical correlation estimation based on covariates with random forests

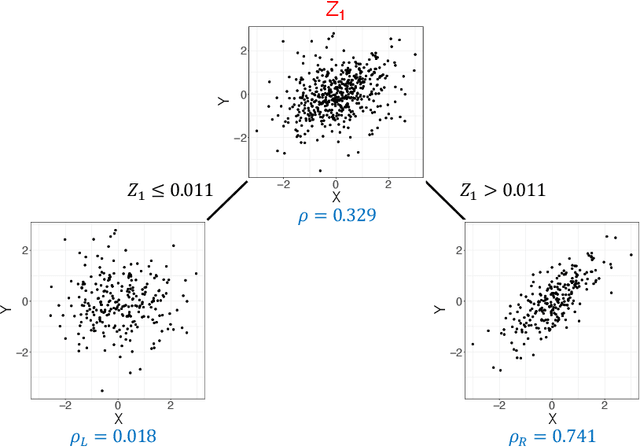
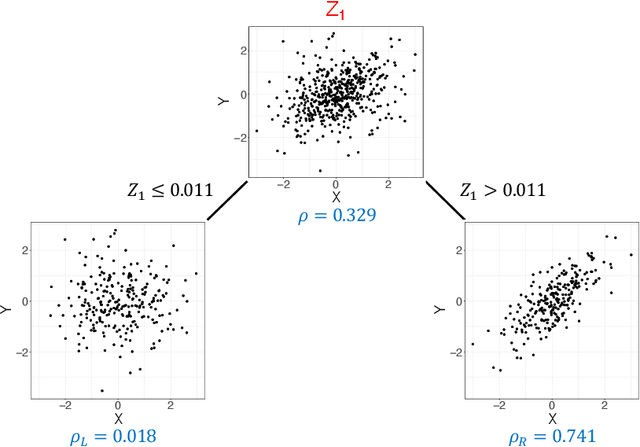
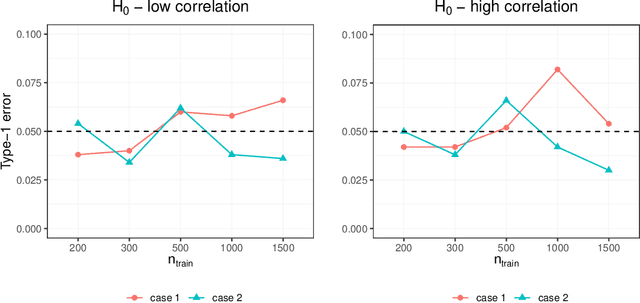
Investigating the relationships between two sets of variables helps to understand their interactions and can be done with canonical correlation analysis (CCA). However, the correlation between the two sets can sometimes depend on a third set of covariates, often subject-related ones such as age, gender, or other clinical measures. In this case, applying CCA to the whole population is not optimal and methods to estimate conditional CCA, given the covariates, can be useful. We propose a new method called Random Forest with Canonical Correlation Analysis (RFCCA) to estimate the conditional canonical correlations between two sets of variables given subject-related covariates. The individual trees in the forest are built with a splitting rule specifically designed to partition the data to maximize the canonical correlation heterogeneity between child nodes. We also propose a significance test to detect the global effect of the covariates on the relationship between two sets of variables. The performance of the proposed method and the global significance test is evaluated through simulation studies that show it provides accurate canonical correlation estimations and well-controlled Type-1 error. We also show an application of the proposed method with EEG data.