COD: Learning Conditional Invariant Representation for Domain Adaptation Regression

Aiming to generalize the label knowledge from a source domain with continuous outputs to an unlabeled target domain, Domain Adaptation Regression (DAR) is developed for complex practical learning problems. However, due to the continuity problem in regression, existing conditional distribution alignment theory and methods with discrete prior, which are proven to be effective in classification settings, are no longer applicable. In this work, focusing on the feasibility problems in DAR, we establish the sufficiency theory for the regression model, which shows the generalization error can be sufficiently dominated by the cross-domain conditional discrepancy. Further, to characterize conditional discrepancy with continuous conditioning variable, a novel Conditional Operator Discrepancy (COD) is proposed, which admits the metric property on conditional distributions via the kernel embedding theory. Finally, to minimize the discrepancy, a COD-based conditional invariant representation learning model is proposed, and the reformulation is derived to show that reasonable modifications on moment statistics can further improve the discriminability of the adaptation model. Extensive experiments on standard DAR datasets verify the validity of theoretical results and the superiority over SOTA DAR methods.

When Invariant Representation Learning Meets Label Shift: Insufficiency and Theoretical Insights

As a crucial step toward real-world learning scenarios with changing environments, dataset shift theory and invariant representation learning algorithm have been extensively studied to relax the identical distribution assumption in classical learning setting. Among the different assumptions on the essential of shifting distributions, generalized label shift (GLS) is the latest developed one which shows great potential to deal with the complex factors within the shift. In this paper, we aim to explore the limitations of current dataset shift theory and algorithm, and further provide new insights by presenting a comprehensive understanding of GLS. From theoretical aspect, two informative generalization bounds are derived, and the GLS learner is proved to be sufficiently close to optimal target model from the Bayesian perspective. The main results show the insufficiency of invariant representation learning, and prove the sufficiency and necessity of GLS correction for generalization, which provide theoretical supports and innovations for exploring generalizable model under dataset shift. From methodological aspect, we provide a unified view of existing shift correction frameworks, and propose a kernel embedding-based correction algorithm (KECA) to minimize the generalization error and achieve successful knowledge transfer. Both theoretical results and extensive experiment evaluations demonstrate the sufficiency and necessity of GLS correction for addressing dataset shift and the superiority of proposed algorithm.

Maximizing Conditional Independence for Unsupervised Domain Adaptation

Unsupervised domain adaptation studies how to transfer a learner from a labeled source domain to an unlabeled target domain with different distributions. Existing methods mainly focus on matching the marginal distributions of the source and target domains, which probably lead a misalignment of samples from the same class but different domains. In this paper, we deal with this misalignment by achieving the class-conditioned transferring from a new perspective. We aim to maximize the conditional independence of feature and domain given class in the reproducing kernel Hilbert space. The optimization of the conditional independence measure can be viewed as minimizing a surrogate of a certain mutual information between feature and domain. An interpretable empirical estimation of the conditional dependence is deduced and connected with the unconditional case. Besides, we provide an upper bound on the target error by taking the class-conditional distribution into account, which provides a new theoretical insight for most class-conditioned transferring methods. In addition to unsupervised domain adaptation, we extend our method to the multi-source scenario in a natural and elegant way. Extensive experiments on four benchmarks validate the effectiveness of the proposed models in both unsupervised domain adaptation and multiple source domain adaptation.

Generalized Label Shift Correction via Minimum Uncertainty Principle: Theory and Algorithm

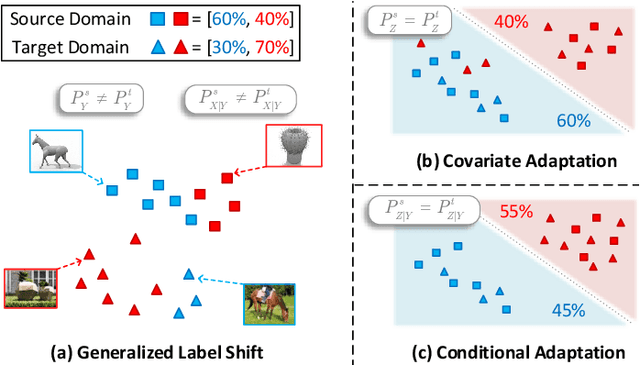
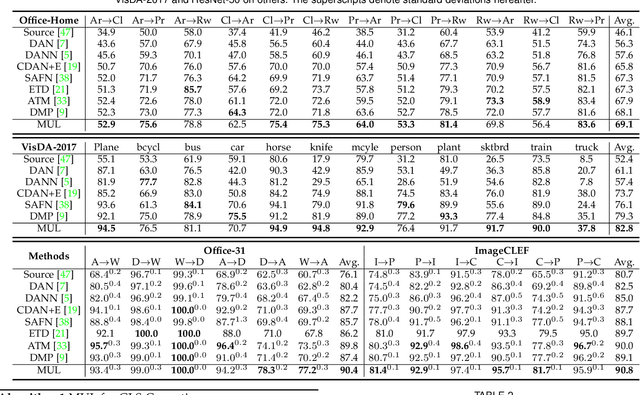
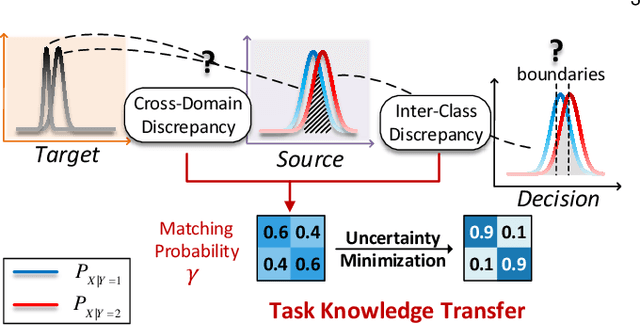
As a fundamental problem in machine learning, dataset shift induces a paradigm to learn and transfer knowledge under changing environment. Previous methods assume the changes are induced by covariate, which is less practical for complex real-world data. We consider the Generalized Label Shift (GLS), which provides an interpretable insight into the learning and transfer of desirable knowledge. Current GLS methods: 1) are not well-connected with the statistical learning theory; 2) usually assume the shifting conditional distributions will be matched with an implicit transformation, but its explicit modeling is unexplored. In this paper, we propose a conditional adaptation framework to deal with these challenges. From the perspective of learning theory, we prove that the generalization error of conditional adaptation is lower than previous covariate adaptation. Following the theoretical results, we propose the minimum uncertainty principle to learn conditional invariant transformation via discrepancy optimization. Specifically, we propose the \textit{conditional metric operator} on Hilbert space to characterize the distinctness of conditional distributions. For finite observations, we prove that the empirical estimation is always well-defined and will converge to underlying truth as sample size increases. The results of extensive experiments demonstrate that the proposed model achieves competitive performance under different GLS scenarios.

Geometry-Aware Unsupervised Domain Adaptation

Unsupervised Domain Adaptation (UDA) aims to transfer the knowledge from the labeled source domain to the unlabeled target domain in the presence of dataset shift. Most existing methods cannot address the domain alignment and class discrimination well, which may distort the intrinsic data structure for downstream tasks (e.g., classification). To this end, we propose a novel geometry-aware model to learn the transferability and discriminability simultaneously via nuclear norm optimization. We introduce the domain coherence and class orthogonality for UDA from the perspective of subspace geometry. The domain coherence will ensure the model has a larger capacity for learning separable representations, and class orthogonality will minimize the correlation between clusters to alleviate the misalignment. So, they are consistent and can benefit from each other. Besides, we provide a theoretical insight into the norm-based learning literature in UDA, which ensures the interpretability of our model. We show that the norms of domains and clusters are expected to be larger and smaller to enhance the transferability and discriminability, respectively. Extensive experimental results on standard UDA datasets demonstrate the effectiveness of our theory and model.

Conditional Bures Metric for Domain Adaptation

As a vital problem in classification-oriented transfer, unsupervised domain adaptation (UDA) has attracted widespread attention in recent years. Previous UDA methods assume the marginal distributions of different domains are shifted while ignoring the discriminant information in the label distributions. This leads to classification performance degeneration in real applications. In this work, we focus on the conditional distribution shift problem which is of great concern to current conditional invariant models. We aim to seek a kernel covariance embedding for conditional distribution which remains yet unexplored. Theoretically, we propose the Conditional Kernel Bures (CKB) metric for characterizing conditional distribution discrepancy, and derive an empirical estimation for the CKB metric without introducing the implicit kernel feature map. It provides an interpretable approach to understand the knowledge transfer mechanism. The established consistency theory of the empirical estimation provides a theoretical guarantee for convergence. A conditional distribution matching network is proposed to learn the conditional invariant and discriminative features for UDA. Extensive experiments and analysis show the superiority of our proposed model.

Unsupervised Domain Adaptation via Discriminative Manifold Propagation

Unsupervised domain adaptation is effective in leveraging rich information from a labeled source domain to an unlabeled target domain. Though deep learning and adversarial strategy made a significant breakthrough in the adaptability of features, there are two issues to be further studied. First, hard-assigned pseudo labels on the target domain are arbitrary and error-prone, and direct application of them may destroy the intrinsic data structure. Second, batch-wise training of deep learning limits the characterization of the global structure. In this paper, a Riemannian manifold learning framework is proposed to achieve transferability and discriminability simultaneously. For the first issue, this framework establishes a probabilistic discriminant criterion on the target domain via soft labels. Based on pre-built prototypes, this criterion is extended to a global approximation scheme for the second issue. Manifold metric alignment is adopted to be compatible with the embedding space. The theoretical error bounds of different alignment metrics are derived for constructive guidance. The proposed method can be used to tackle a series of variants of domain adaptation problems, including both vanilla and partial settings. Extensive experiments have been conducted to investigate the method and a comparative study shows the superiority of the discriminative manifold learning framework.

Discriminative Residual Analysis for Image Set Classification with Posture and Age Variations

Image set recognition has been widely applied in many practical problems like real-time video retrieval and image caption tasks. Due to its superior performance, it has grown into a significant topic in recent years. However, images with complicated variations, e.g., postures and human ages, are difficult to address, as these variations are continuous and gradual with respect to image appearance. Consequently, the crucial point of image set recognition is to mine the intrinsic connection or structural information from the image batches with variations. In this work, a Discriminant Residual Analysis (DRA) method is proposed to improve the classification performance by discovering discriminant features in related and unrelated groups. Specifically, DRA attempts to obtain a powerful projection which casts the residual representations into a discriminant subspace. Such a projection subspace is expected to magnify the useful information of the input space as much as possible, then the relation between the training set and the test set described by the given metric or distance will be more precise in the discriminant subspace. We also propose a nonfeasance strategy by defining another approach to construct the unrelated groups, which help to reduce furthermore the cost of sampling errors. Two regularization approaches are used to deal with the probable small sample size problem. Extensive experiments are conducted on benchmark databases, and the results show superiority and efficiency of the new methods.

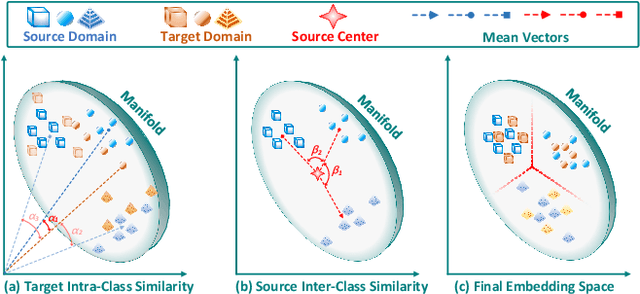
Unsupervised Domain Adaptation via Discriminative Manifold Embedding and Alignment

Unsupervised domain adaptation is effective in leveraging the rich information from the source domain to the unsupervised target domain. Though deep learning and adversarial strategy make an important breakthrough in the adaptability of features, there are two issues to be further explored. First, the hard-assigned pseudo labels on the target domain are risky to the intrinsic data structure. Second, the batch-wise training manner in deep learning limits the description of the global structure. In this paper, a Riemannian manifold learning framework is proposed to achieve transferability and discriminability consistently. As to the first problem, this method establishes a probabilistic discriminant criterion on the target domain via soft labels. Further, this criterion is extended to a global approximation scheme for the second issue; such approximation is also memory-saving. The manifold metric alignment is exploited to be compatible with the embedding space. A theoretical error bound is derived to facilitate the alignment. Extensive experiments have been conducted to investigate the proposal and results of the comparison study manifest the superiority of consistent manifold learning framework.