Bures Joint Distribution Alignment with Dynamic Margin for Unsupervised Domain Adaptation

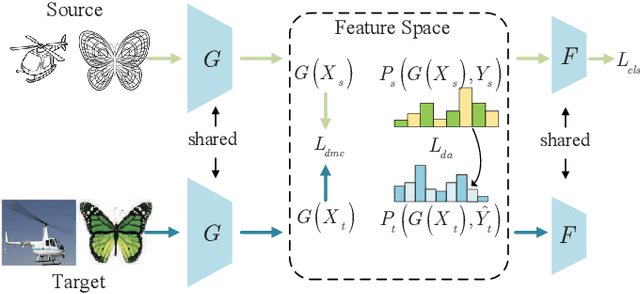
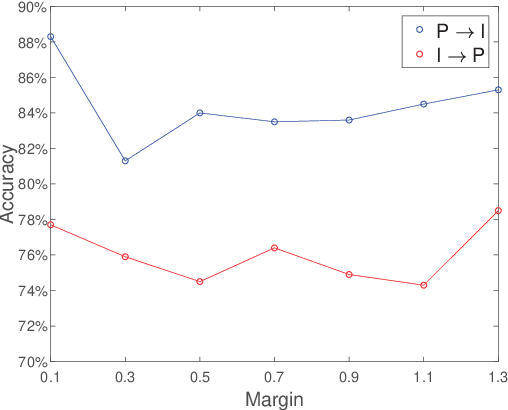
Unsupervised domain adaptation (UDA) is one of the prominent tasks of transfer learning, and it provides an effective approach to mitigate the distribution shift between the labeled source domain and the unlabeled target domain. Prior works mainly focus on aligning the marginal distributions or the estimated class-conditional distributions. However, the joint dependency among the feature and the label is crucial for the adaptation task and is not fully exploited. To address this problem, we propose the Bures Joint Distribution Alignment (BJDA) algorithm which directly models the joint distribution shift based on the optimal transport theory in the infinite-dimensional kernel spaces. Specifically, we propose a novel alignment loss term that minimizes the kernel Bures-Wasserstein distance between the joint distributions. Technically, BJDA can effectively capture the nonlinear structures underlying the data. In addition, we introduce a dynamic margin in contrastive learning phase to flexibly characterize the class separability and improve the discriminative ability of representations. It also avoids the cross-validation procedure to determine the margin parameter in traditional triplet loss based methods. Extensive experiments show that BJDA is very effective for the UDA tasks, as it outperforms state-of-the-art algorithms in most experimental settings. In particular, BJDA improves the average accuracy of UDA tasks by 2.8% on Adaptiope, 1.4% on Office-Caltech10, and 1.1% on ImageCLEF-DA.

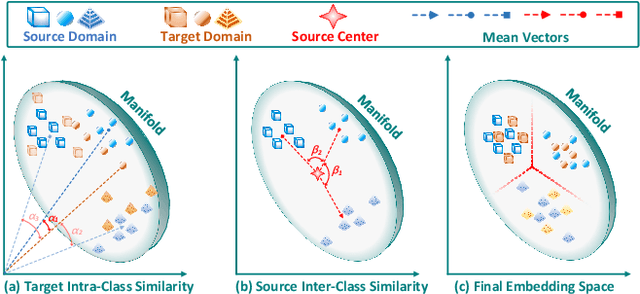
Unsupervised Domain Adaptation via Discriminative Manifold Embedding and Alignment

Unsupervised domain adaptation is effective in leveraging the rich information from the source domain to the unsupervised target domain. Though deep learning and adversarial strategy make an important breakthrough in the adaptability of features, there are two issues to be further explored. First, the hard-assigned pseudo labels on the target domain are risky to the intrinsic data structure. Second, the batch-wise training manner in deep learning limits the description of the global structure. In this paper, a Riemannian manifold learning framework is proposed to achieve transferability and discriminability consistently. As to the first problem, this method establishes a probabilistic discriminant criterion on the target domain via soft labels. Further, this criterion is extended to a global approximation scheme for the second issue; such approximation is also memory-saving. The manifold metric alignment is exploited to be compatible with the embedding space. A theoretical error bound is derived to facilitate the alignment. Extensive experiments have been conducted to investigate the proposal and results of the comparison study manifest the superiority of consistent manifold learning framework.