Low-Tubal-Rank Tensor Recovery via Factorized Gradient Descent
Paper and Code
Feb 03, 2024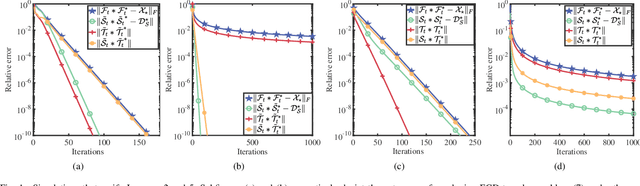
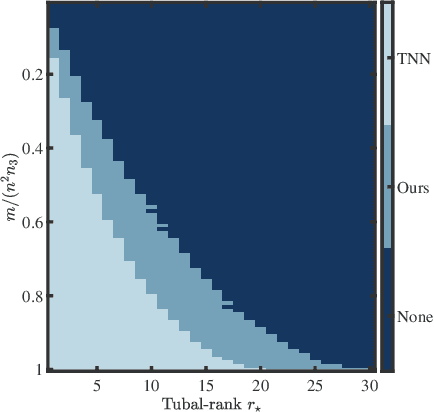
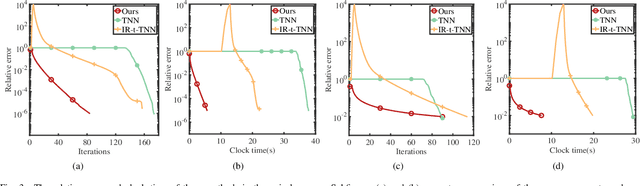
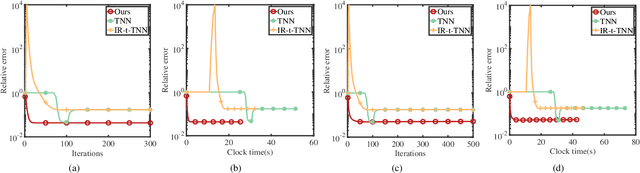
This paper considers the problem of recovering a tensor with an underlying low-tubal-rank structure from a small number of corrupted linear measurements. Traditional approaches tackling such a problem require the computation of tensor Singular Value Decomposition (t-SVD), that is a computationally intensive process, rendering them impractical for dealing with large-scale tensors. Aim to address this challenge, we propose an efficient and effective low-tubal-rank tensor recovery method based on a factorization procedure akin to the Burer-Monteiro (BM) method. Precisely, our fundamental approach involves decomposing a large tensor into two smaller factor tensors, followed by solving the problem through factorized gradient descent (FGD). This strategy eliminates the need for t-SVD computation, thereby reducing computational costs and storage requirements. We provide rigorous theoretical analysis to ensure the convergence of FGD under both noise-free and noisy situations. Additionally, it is worth noting that our method does not require the precise estimation of the tensor tubal-rank. Even in cases where the tubal-rank is slightly overestimated, our approach continues to demonstrate robust performance. A series of experiments have been carried out to demonstrate that, as compared to other popular ones, our approach exhibits superior performance in multiple scenarios, in terms of the faster computational speed and the smaller convergence error.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge