Nonstationary Temporal Matrix Factorization for Multivariate Time Series Forecasting
Paper and Code
Mar 20, 2022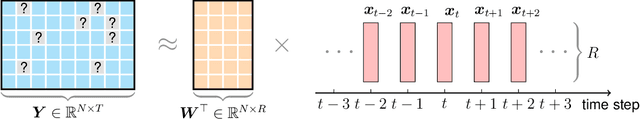
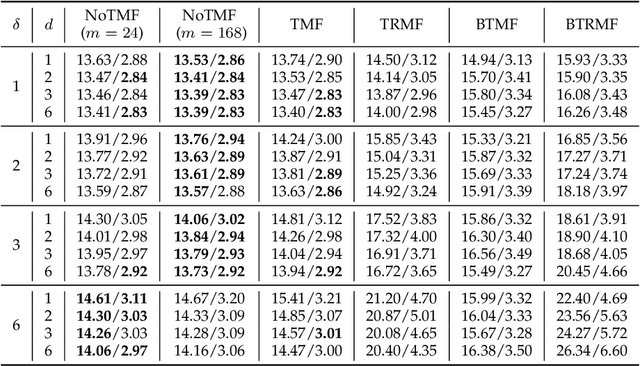
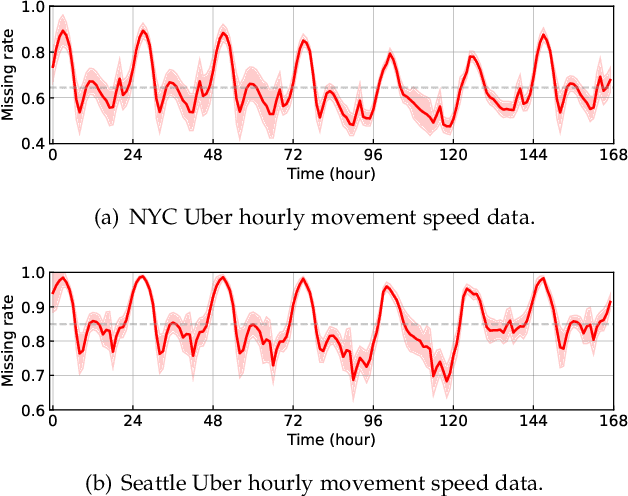
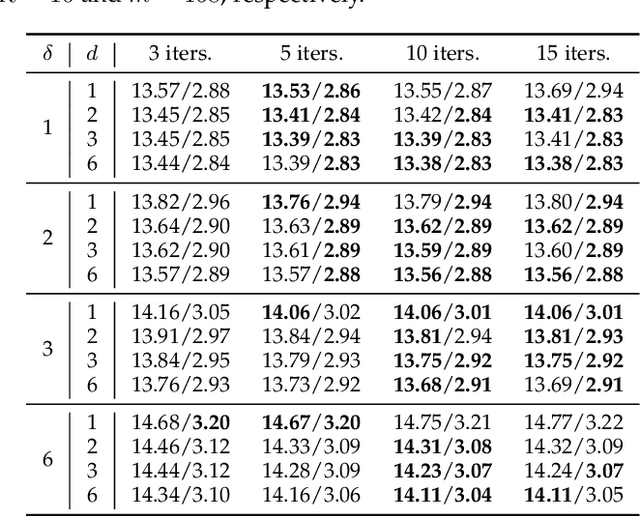
Modern time series datasets are often high-dimensional, incomplete/sparse, and nonstationary. These properties hinder the development of scalable and efficient solutions for time series forecasting and analysis. To address these challenges, we propose a Nonstationary Temporal Matrix Factorization (NoTMF) model, in which matrix factorization is used to reconstruct the whole time series matrix and vector autoregressive (VAR) process is imposed on a properly differenced copy of the temporal factor matrix. This approach not only preserves the low-rank property of the data but also offers consistent temporal dynamics. The learning process of NoTMF involves the optimization of two factor matrices and a collection of VAR coefficient matrices. To efficiently solve the optimization problem, we derive an alternating minimization framework, in which subproblems are solved using conjugate gradient and least squares methods. In particular, the use of conjugate gradient method offers an efficient routine and allows us to apply NoTMF on large-scale problems. Through extensive experiments on Uber movement speed dataset, we demonstrate the superior accuracy and effectiveness of NoTMF over other baseline models. Our results also confirm the importance of addressing the nonstationarity of real-world time series data such as spatiotemporal traffic flow/speed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge