Accelerating Large-Scale Regularized High-Order Tensor Recovery

Currently, existing tensor recovery methods fail to recognize the impact of tensor scale variations on their structural characteristics. Furthermore, existing studies face prohibitive computational costs when dealing with large-scale high-order tensor data. To alleviate these issue, assisted by the Krylov subspace iteration, block Lanczos bidiagonalization process, and random projection strategies, this article first devises two fast and accurate randomized algorithms for low-rank tensor approximation (LRTA) problem. Theoretical bounds on the accuracy of the approximation error estimate are established. Next, we develop a novel generalized nonconvex modeling framework tailored to large-scale tensor recovery, in which a new regularization paradigm is exploited to achieve insightful prior representation for large-scale tensors. On the basis of the above, we further investigate new unified nonconvex models and efficient optimization algorithms, respectively, for several typical high-order tensor recovery tasks in unquantized and quantized situations. To render the proposed algorithms practical and efficient for large-scale tensor data, the proposed randomized LRTA schemes are integrated into their central and time-intensive computations. Finally, we conduct extensive experiments on various large-scale tensors, whose results demonstrate the practicability, effectiveness and superiority of the proposed method in comparison with some state-of-the-art approaches.

Hyperspectral Anomaly Detection Fused Unified Nonconvex Tensor Ring Factors Regularization

In recent years, tensor decomposition-based approaches for hyperspectral anomaly detection (HAD) have gained significant attention in the field of remote sensing. However, existing methods often fail to fully leverage both the global correlations and local smoothness of the background components in hyperspectral images (HSIs), which exist in both the spectral and spatial domains. This limitation results in suboptimal detection performance. To mitigate this critical issue, we put forward a novel HAD method named HAD-EUNTRFR, which incorporates an enhanced unified nonconvex tensor ring (TR) factors regularization. In the HAD-EUNTRFR framework, the raw HSIs are first decomposed into background and anomaly components. The TR decomposition is then employed to capture the spatial-spectral correlations within the background component. Additionally, we introduce a unified and efficient nonconvex regularizer, induced by tensor singular value decomposition (TSVD), to simultaneously encode the low-rankness and sparsity of the 3-D gradient TR factors into a unique concise form. The above characterization scheme enables the interpretable gradient TR factors to inherit the low-rankness and smoothness of the original background. To further enhance anomaly detection, we design a generalized nonconvex regularization term to exploit the group sparsity of the anomaly component. To solve the resulting doubly nonconvex model, we develop a highly efficient optimization algorithm based on the alternating direction method of multipliers (ADMM) framework. Experimental results on several benchmark datasets demonstrate that our proposed method outperforms existing state-of-the-art (SOTA) approaches in terms of detection accuracy.

Nonconvex Robust High-Order Tensor Completion Using Randomized Low-Rank Approximation

Within the tensor singular value decomposition (T-SVD) framework, existing robust low-rank tensor completion approaches have made great achievements in various areas of science and engineering. Nevertheless, these methods involve the T-SVD based low-rank approximation, which suffers from high computational costs when dealing with large-scale tensor data. Moreover, most of them are only applicable to third-order tensors. Against these issues, in this article, two efficient low-rank tensor approximation approaches fusing randomized techniques are first devised under the order-d (d >= 3) T-SVD framework. On this basis, we then further investigate the robust high-order tensor completion (RHTC) problem, in which a double nonconvex model along with its corresponding fast optimization algorithms with convergence guarantees are developed. To the best of our knowledge, this is the first study to incorporate the randomized low-rank approximation into the RHTC problem. Empirical studies on large-scale synthetic and real tensor data illustrate that the proposed method outperforms other state-of-the-art approaches in terms of both computational efficiency and estimated precision.

Guaranteed Tensor Recovery Fused Low-rankness and Smoothness

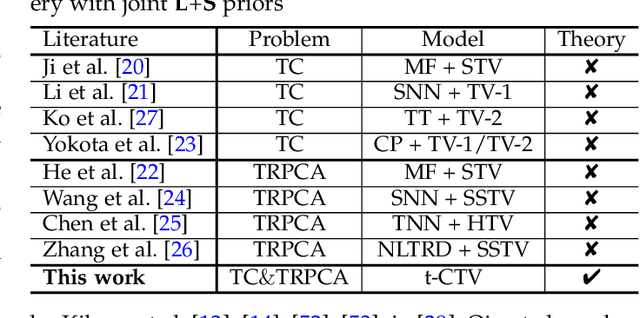
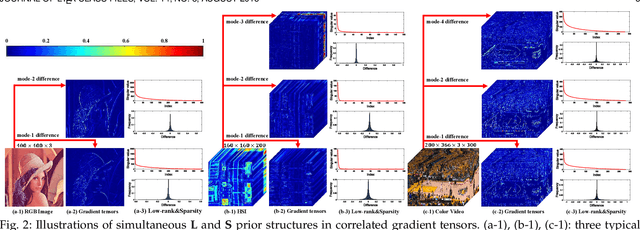
The tensor data recovery task has thus attracted much research attention in recent years. Solving such an ill-posed problem generally requires to explore intrinsic prior structures underlying tensor data, and formulate them as certain forms of regularization terms for guiding a sound estimate of the restored tensor. Recent research have made significant progress by adopting two insightful tensor priors, i.e., global low-rankness (L) and local smoothness (S) across different tensor modes, which are always encoded as a sum of two separate regularization terms into the recovery models. However, unlike the primary theoretical developments on low-rank tensor recovery, these joint L+S models have no theoretical exact-recovery guarantees yet, making the methods lack reliability in real practice. To this crucial issue, in this work, we build a unique regularization term, which essentially encodes both L and S priors of a tensor simultaneously. Especially, by equipping this single regularizer into the recovery models, we can rigorously prove the exact recovery guarantees for two typical tensor recovery tasks, i.e., tensor completion (TC) and tensor robust principal component analysis (TRPCA). To the best of our knowledge, this should be the first exact-recovery results among all related L+S methods for tensor recovery. Significant recovery accuracy improvements over many other SOTA methods in several TC and TRPCA tasks with various kinds of visual tensor data are observed in extensive experiments. Typically, our method achieves a workable performance when the missing rate is extremely large, e.g., 99.5%, for the color image inpainting task, while all its peers totally fail in such challenging case.

Exact Decomposition of Joint Low Rankness and Local Smoothness Plus Sparse Matrices

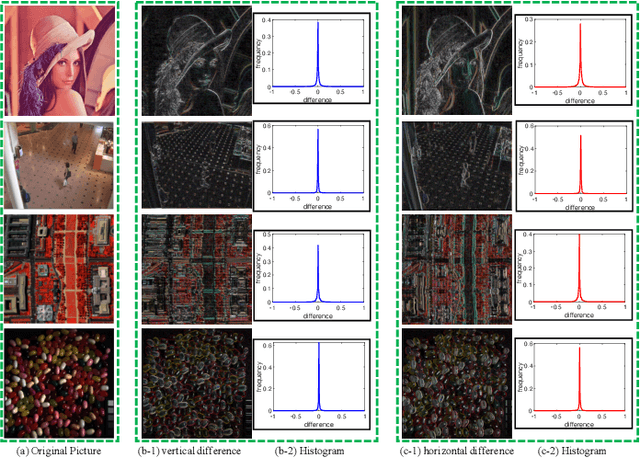
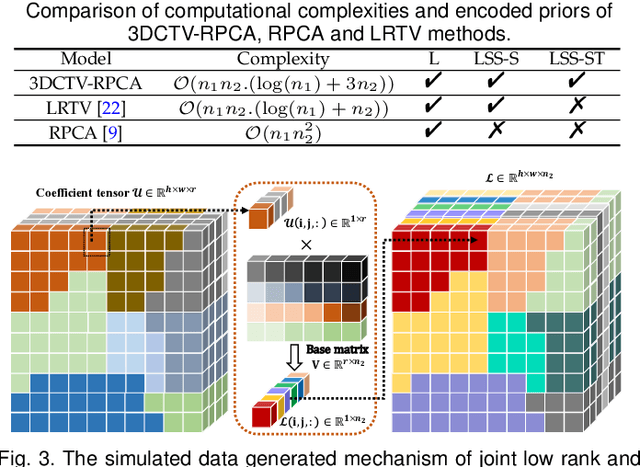
It is known that the decomposition in low-rank and sparse matrices (\textbf{L+S} for short) can be achieved by several Robust PCA techniques. Besides the low rankness, the local smoothness (\textbf{LSS}) is a vitally essential prior for many real-world matrix data such as hyperspectral images and surveillance videos, which makes such matrices have low-rankness and local smoothness properties at the same time. This poses an interesting question: Can we make a matrix decomposition in terms of \textbf{L\&LSS +S } form exactly? To address this issue, we propose in this paper a new RPCA model based on three-dimensional correlated total variation regularization (3DCTV-RPCA for short) by fully exploiting and encoding the prior expression underlying such joint low-rank and local smoothness matrices. Specifically, using a modification of Golfing scheme, we prove that under some mild assumptions, the proposed 3DCTV-RPCA model can decompose both components exactly, which should be the first theoretical guarantee among all such related methods combining low rankness and local smoothness. In addition, by utilizing Fast Fourier Transform (FFT), we propose an efficient ADMM algorithm with a solid convergence guarantee for solving the resulting optimization problem. Finally, a series of experiments on both simulations and real applications are carried out to demonstrate the general validity of the proposed 3DCTV-RPCA model.

Tensor Restricted Isometry Property Analysis For a Large Class of Random Measurement Ensembles

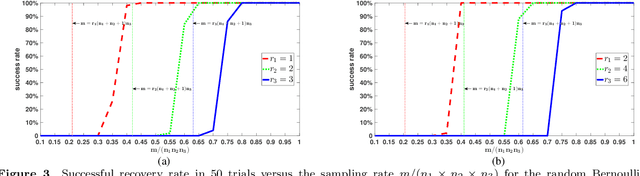
In previous work, theoretical analysis based on the tensor Restricted Isometry Property (t-RIP) established the robust recovery guarantees of a low-tubal-rank tensor. The obtained sufficient conditions depend strongly on the assumption that the linear measurement maps satisfy the t-RIP. In this paper, by exploiting the probabilistic arguments, we prove that such linear measurement maps exist under suitable conditions on the number of measurements in terms of the tubal rank r and the size of third-order tensor n1, n2, n3. And the obtained minimal possible number of linear measurements is nearly optimal compared with the degrees of freedom of a tensor with tubal rank r. Specially, we consider a random sub-Gaussian distribution that includes Gaussian, Bernoulli and all bounded distributions and construct a large class of linear maps that satisfy a t-RIP with high probability. Moreover, the validity of the required number of measurements is verified by numerical experiments.