Cross-view geo-localization, Image retrieval, Multiscale geometric modeling, Frequency domain enhancement

Cross-view geo-localization (CVGL) aims to establish spatial correspondences between images captured from significantly different viewpoints and constitutes a fundamental technique for visual localization in GNSS-denied environments. Nevertheless, CVGL remains challenging due to severe geometric asymmetry, texture inconsistency across imaging domains, and the progressive degradation of discriminative local information. Existing methods predominantly rely on spatial domain feature alignment, which is inherently sensitive to large scale viewpoint variations and local disturbances. To alleviate these limitations, this paper proposes the Spatial and Frequency Domain Enhancement Network (SFDE), which leverages complementary representations from spatial and frequency domains. SFDE adopts a three branch parallel architecture to model global semantic context, local geometric structure, and statistical stability in the frequency domain, respectively, thereby characterizing consistency across domains from the perspectives of scene topology, multiscale structural patterns, and frequency invariance. The resulting complementary features are jointly optimized in a unified embedding space via progressive enhancement and coupled constraints, enabling the learning of cross-view representations with consistency across multiple granularities. Comprehensive experiments show that SFDE achieves competitive performance and in many cases even surpasses state-of-the-art methods, while maintaining a lightweight and computationally efficient design. {Our code is available at https://github.com/Mashuaishuai669/SFDE

A Hypernetwork Based Framework for Non-Stationary Channel Prediction

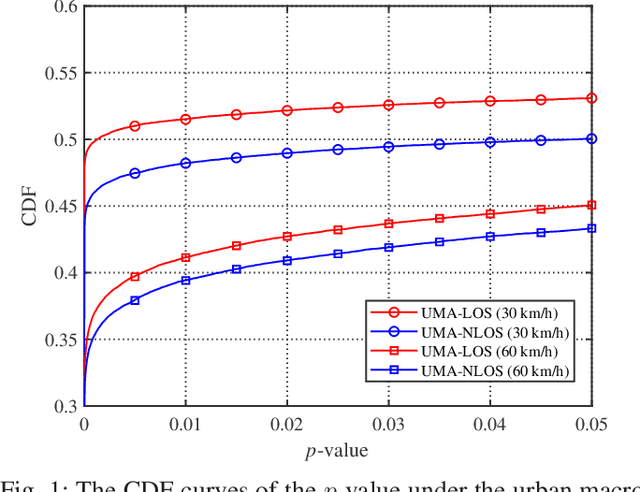
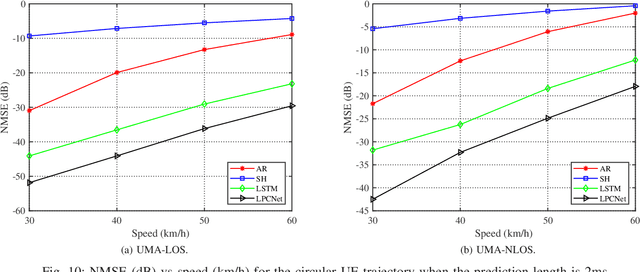
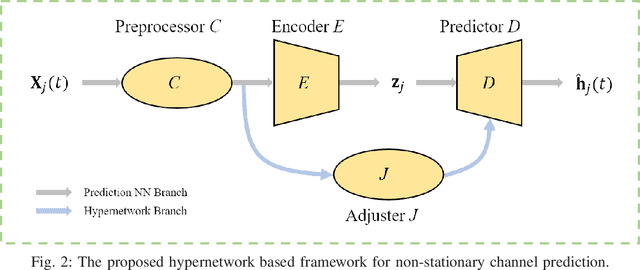
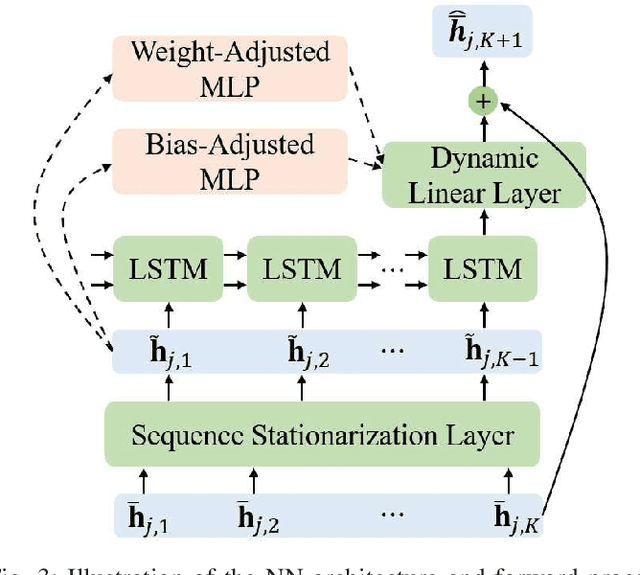
In order to break through the development bottleneck of modern wireless communication networks, a critical issue is the out-of-date channel state information (CSI) in high mobility scenarios. In general, non-stationary CSI has statistical properties which vary with time, implying that the data distribution changes continuously over time. This temporal distribution shift behavior undermines the accurate channel prediction and it is still an open problem in the related literature. In this paper, a hypernetwork based framework is proposed for non-stationary channel prediction. The framework aims to dynamically update the neural network (NN) parameters as the wireless channel changes to automatically adapt to various input CSI distributions. Based on this framework, we focus on low-complexity hypernetwork design and present a deep learning (DL) based channel prediction method, termed as LPCNet, which improves the CSI prediction accuracy with acceptable complexity. Moreover, to maximize the achievable downlink spectral efficiency (SE), a joint channel prediction and beamforming (BF) method is developed, termed as JLPCNet, which seeks to predict the BF vector. Our numerical results showcase the effectiveness and flexibility of the proposed framework, and demonstrate the superior performance of LPCNet and JLPCNet in various scenarios for fixed and varying user speeds.

Exact Decomposition of Joint Low Rankness and Local Smoothness Plus Sparse Matrices

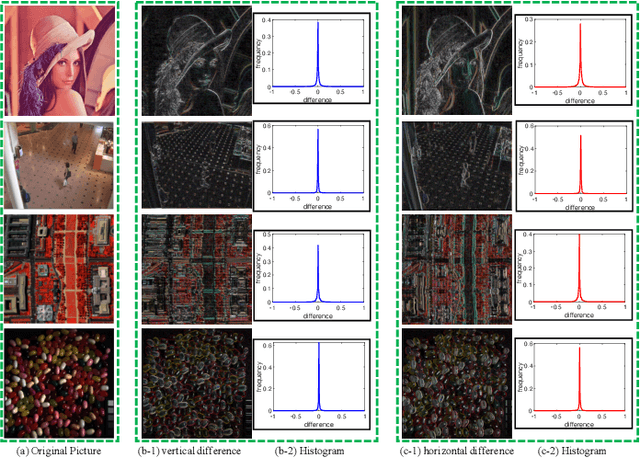
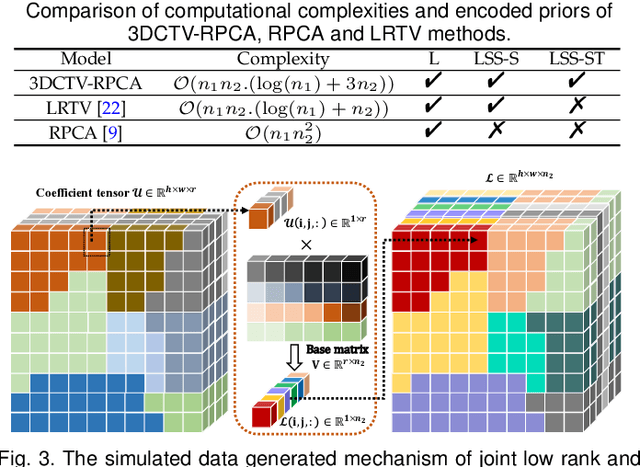
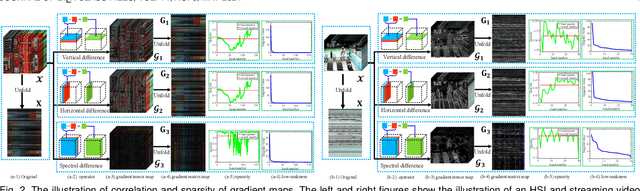
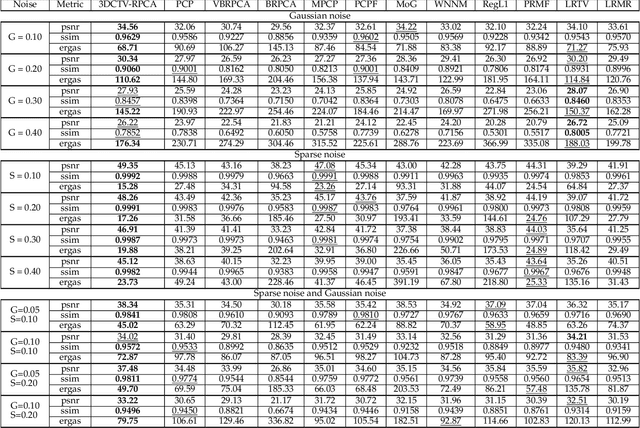
It is known that the decomposition in low-rank and sparse matrices (\textbf{L+S} for short) can be achieved by several Robust PCA techniques. Besides the low rankness, the local smoothness (\textbf{LSS}) is a vitally essential prior for many real-world matrix data such as hyperspectral images and surveillance videos, which makes such matrices have low-rankness and local smoothness properties at the same time. This poses an interesting question: Can we make a matrix decomposition in terms of \textbf{L\&LSS +S } form exactly? To address this issue, we propose in this paper a new RPCA model based on three-dimensional correlated total variation regularization (3DCTV-RPCA for short) by fully exploiting and encoding the prior expression underlying such joint low-rank and local smoothness matrices. Specifically, using a modification of Golfing scheme, we prove that under some mild assumptions, the proposed 3DCTV-RPCA model can decompose both components exactly, which should be the first theoretical guarantee among all such related methods combining low rankness and local smoothness. In addition, by utilizing Fast Fourier Transform (FFT), we propose an efficient ADMM algorithm with a solid convergence guarantee for solving the resulting optimization problem. Finally, a series of experiments on both simulations and real applications are carried out to demonstrate the general validity of the proposed 3DCTV-RPCA model.