Adaptive Query Prompting for Multi-Domain Landmark Detection

Medical landmark detection is crucial in various medical imaging modalities and procedures. Although deep learning-based methods have achieve promising performance, they are mostly designed for specific anatomical regions or tasks. In this work, we propose a universal model for multi-domain landmark detection by leveraging transformer architecture and developing a prompting component, named as Adaptive Query Prompting (AQP). Instead of embedding additional modules in the backbone network, we design a separate module to generate prompts that can be effectively extended to any other transformer network. In our proposed AQP, prompts are learnable parameters maintained in a memory space called prompt pool. The central idea is to keep the backbone frozen and then optimize prompts to instruct the model inference process. Furthermore, we employ a lightweight decoder to decode landmarks from the extracted features, namely Light-MLD. Thanks to the lightweight nature of the decoder and AQP, we can handle multiple datasets by sharing the backbone encoder and then only perform partial parameter tuning without incurring much additional cost. It has the potential to be extended to more landmark detection tasks. We conduct experiments on three widely used X-ray datasets for different medical landmark detection tasks. Our proposed Light-MLD coupled with AQP achieves SOTA performance on many metrics even without the use of elaborate structural designs or complex frameworks.

Tensor Restricted Isometry Property Analysis For a Large Class of Random Measurement Ensembles

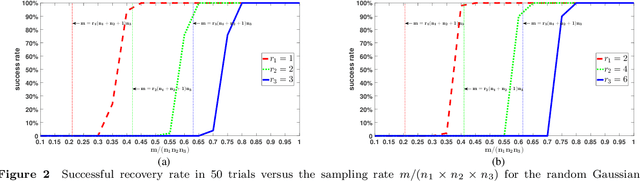
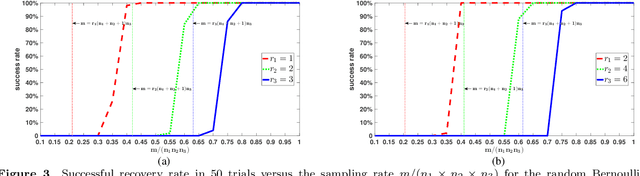
In previous work, theoretical analysis based on the tensor Restricted Isometry Property (t-RIP) established the robust recovery guarantees of a low-tubal-rank tensor. The obtained sufficient conditions depend strongly on the assumption that the linear measurement maps satisfy the t-RIP. In this paper, by exploiting the probabilistic arguments, we prove that such linear measurement maps exist under suitable conditions on the number of measurements in terms of the tubal rank r and the size of third-order tensor n1, n2, n3. And the obtained minimal possible number of linear measurements is nearly optimal compared with the degrees of freedom of a tensor with tubal rank r. Specially, we consider a random sub-Gaussian distribution that includes Gaussian, Bernoulli and all bounded distributions and construct a large class of linear maps that satisfy a t-RIP with high probability. Moreover, the validity of the required number of measurements is verified by numerical experiments.