Cesar Caiafa
Alternating Local Enumeration (TnALE): Solving Tensor Network Structure Search with Fewer Evaluations
May 08, 2023
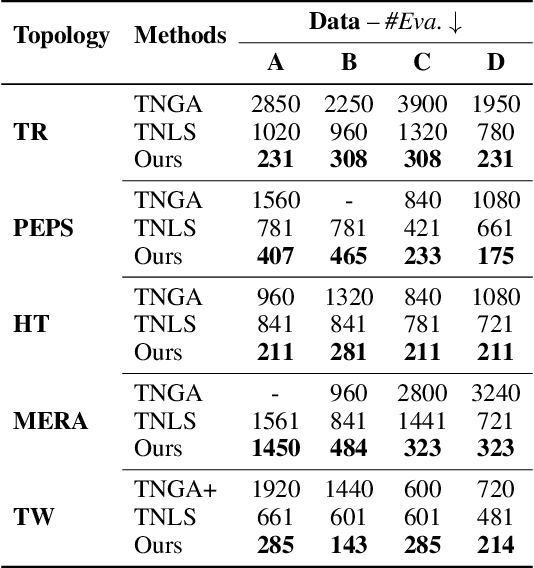
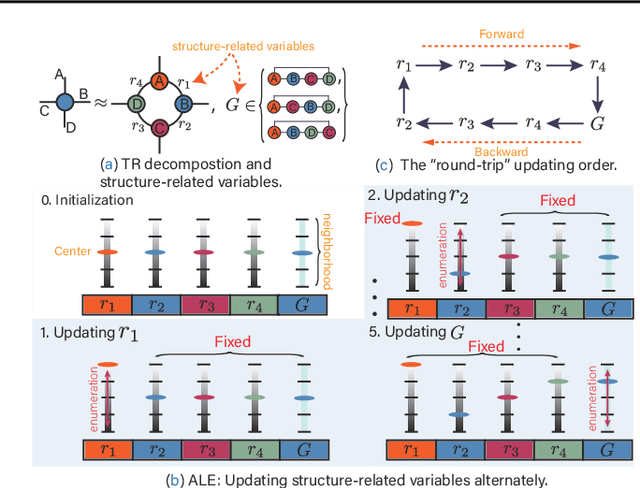
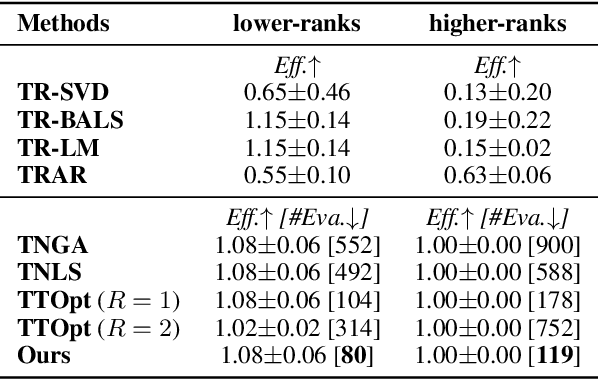
Abstract:Tensor network (TN) is a powerful framework in machine learning, but selecting a good TN model, known as TN structure search (TN-SS), is a challenging and computationally intensive task. The recent approach TNLS~\cite{li2022permutation} showed promising results for this task, however, its computational efficiency is still unaffordable, requiring too many evaluations of the objective function. We propose TnALE, a new algorithm that updates each structure-related variable alternately by local enumeration, \emph{greatly} reducing the number of evaluations compared to TNLS. We theoretically investigate the descent steps for TNLS and TnALE, proving that both algorithms can achieve linear convergence up to a constant if a sufficient reduction of the objective is \emph{reached} in each neighborhood. We also compare the evaluation efficiency of TNLS and TnALE, revealing that $\Omega(2^N)$ evaluations are typically required in TNLS for \emph{reaching} the objective reduction in the neighborhood, while ideally $O(N^2R)$ evaluations are sufficient in TnALE, where $N$ denotes the tensor order and $R$ reflects the \emph{``low-rankness''} of the neighborhood. Experimental results verify that TnALE can find practically good TN-ranks and permutations with vastly fewer evaluations than the state-of-the-art algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge