Transformed Low-Rank Parameterization Can Help Robust Generalization for Tensor Neural Networks

Achieving efficient and robust multi-channel data learning is a challenging task in data science. By exploiting low-rankness in the transformed domain, i.e., transformed low-rankness, tensor Singular Value Decomposition (t-SVD) has achieved extensive success in multi-channel data representation and has recently been extended to function representation such as Neural Networks with t-product layers (t-NNs). However, it still remains unclear how t-SVD theoretically affects the learning behavior of t-NNs. This paper is the first to answer this question by deriving the upper bounds of the generalization error of both standard and adversarially trained t-NNs. It reveals that the t-NNs compressed by exact transformed low-rank parameterization can achieve a sharper adversarial generalization bound. In practice, although t-NNs rarely have exactly transformed low-rank weights, our analysis further shows that by adversarial training with gradient flow (GF), the over-parameterized t-NNs with ReLU activations are trained with implicit regularization towards transformed low-rank parameterization under certain conditions. We also establish adversarial generalization bounds for t-NNs with approximately transformed low-rank weights. Our analysis indicates that the transformed low-rank parameterization can promisingly enhance robust generalization for t-NNs.

SA-MLP: Distilling Graph Knowledge from GNNs into Structure-Aware MLP

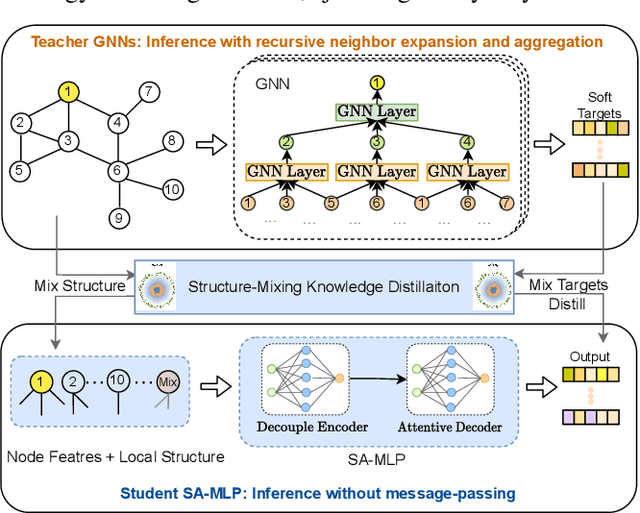
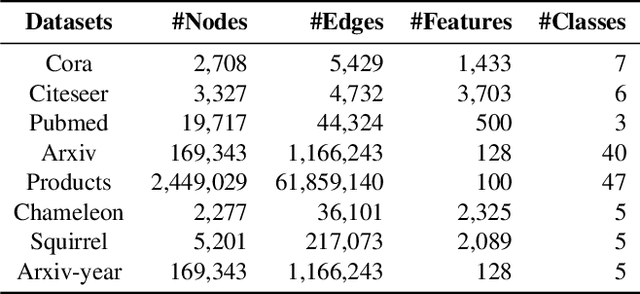
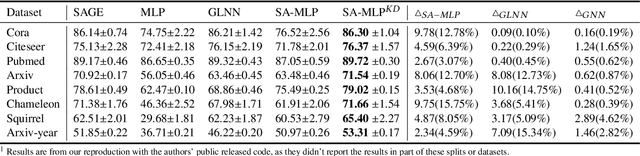
The message-passing mechanism helps Graph Neural Networks (GNNs) achieve remarkable results on various node classification tasks. Nevertheless, the recursive nodes fetching and aggregation in message-passing cause inference latency when deploying GNNs to large-scale graphs. One promising inference acceleration direction is to distill the GNNs into message-passing-free student multi-layer perceptrons (MLPs). However, the MLP student cannot fully learn the structure knowledge due to the lack of structure inputs, which causes inferior performance in the heterophily and inductive scenarios. To address this, we intend to inject structure information into MLP-like students in low-latency and interpretable ways. Specifically, we first design a Structure-Aware MLP (SA-MLP) student that encodes both features and structures without message-passing. Then, we introduce a novel structure-mixing knowledge distillation strategy to enhance the learning ability of MLPs for structure information. Furthermore, we design a latent structure embedding approximation technique with two-stage distillation for inductive scenarios. Extensive experiments on eight benchmark datasets under both transductive and inductive settings show that our SA-MLP can consistently outperform the teacher GNNs, while maintaining faster inference as MLPs. The source code of our work can be found in https://github.com/JC-202/SA-MLP.

Neural Ordinary Differential Equation Model for Evolutionary Subspace Clustering and Its Applications

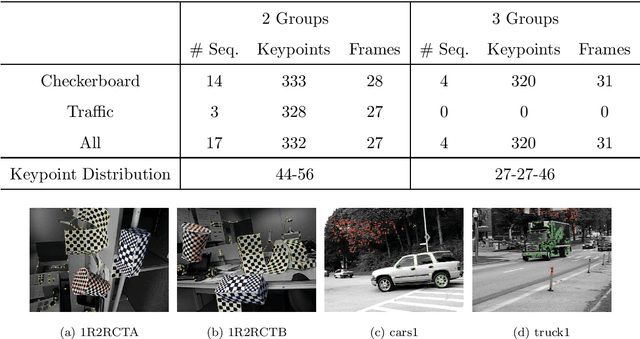
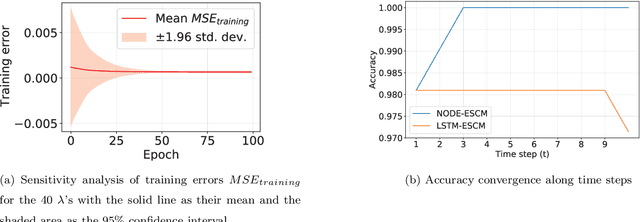
The neural ordinary differential equation (neural ODE) model has attracted increasing attention in time series analysis for its capability to process irregular time steps, i.e., data are not observed over equally-spaced time intervals. In multi-dimensional time series analysis, a task is to conduct evolutionary subspace clustering, aiming at clustering temporal data according to their evolving low-dimensional subspace structures. Many existing methods can only process time series with regular time steps while time series are unevenly sampled in many situations such as missing data. In this paper, we propose a neural ODE model for evolutionary subspace clustering to overcome this limitation and a new objective function with subspace self-expressiveness constraint is introduced. We demonstrate that this method can not only interpolate data at any time step for the evolutionary subspace clustering task, but also achieve higher accuracy than other state-of-the-art evolutionary subspace clustering methods. Both synthetic and real-world data are used to illustrate the efficacy of our proposed method.

Graph Decoupling Attention Markov Networks for Semi-supervised Graph Node Classification

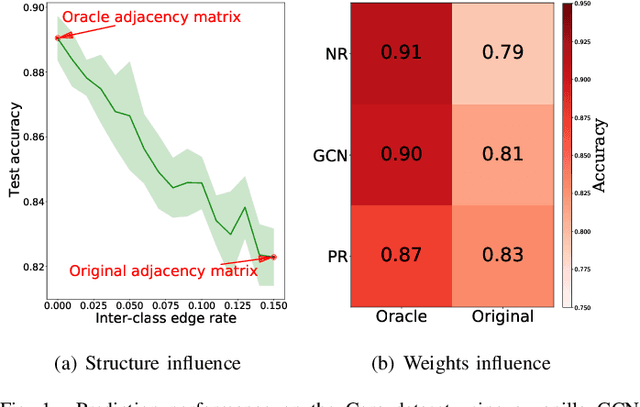
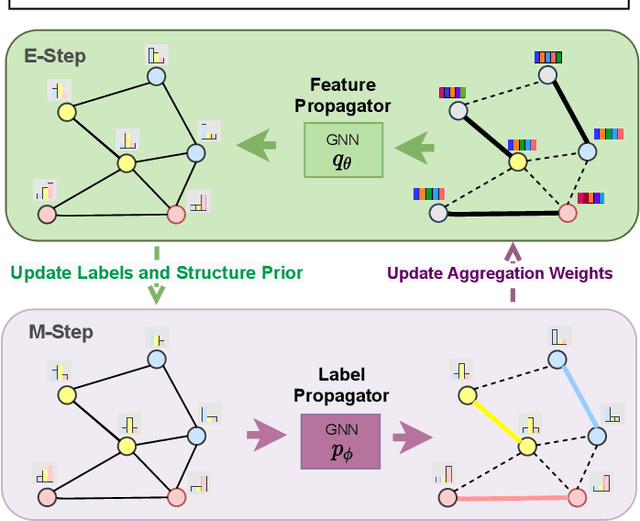
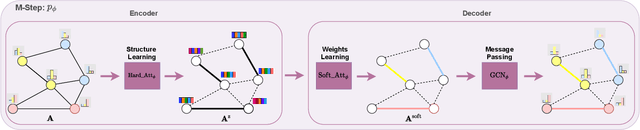
Graph neural networks (GNN) have been ubiquitous in graph learning tasks such as node classification. Most of GNN methods update the node embedding iteratively by aggregating its neighbors' information. However, they often suffer from negative disturbance, due to edges connecting nodes with different labels. One approach to alleviate this negative disturbance is to use attention, but current attention always considers feature similarity and suffers from the lack of supervision. In this paper, we consider the label dependency of graph nodes and propose a decoupling attention mechanism to learn both hard and soft attention. The hard attention is learned on labels for a refined graph structure with fewer inter-class edges. Its purpose is to reduce the aggregation's negative disturbance. The soft attention is learned on features maximizing the information gain by message passing over better graph structures. Moreover, the learned attention guides the label propagation and the feature propagation. Extensive experiments are performed on five well-known benchmark graph datasets to verify the effectiveness of the proposed method.

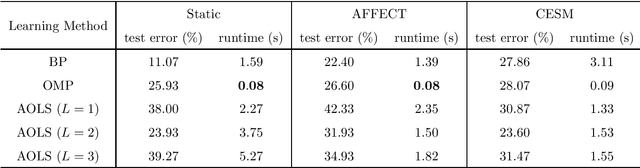
Tensor-Train Parameterization for Ultra Dimensionality Reduction

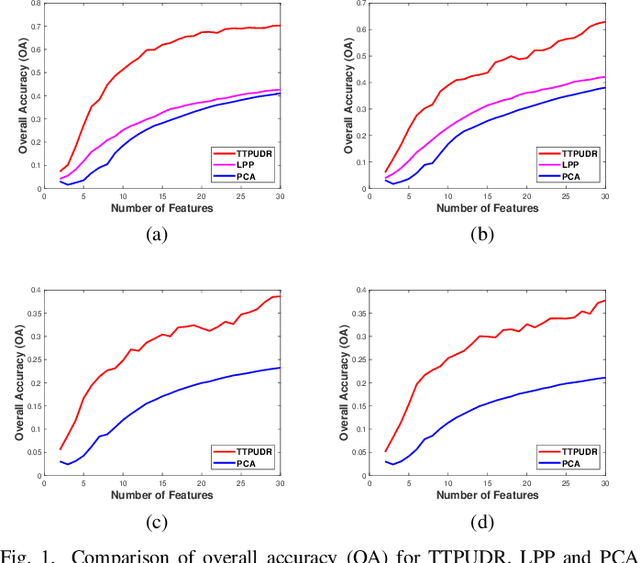
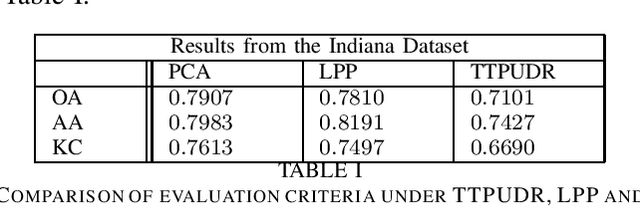
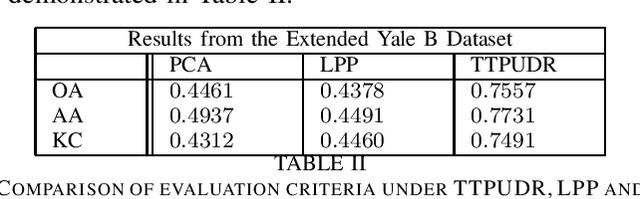
Locality preserving projections (LPP) are a classical dimensionality reduction method based on data graph information. However, LPP is still responsive to extreme outliers. LPP aiming for vectorial data may undermine data structural information when it is applied to multidimensional data. Besides, it assumes the dimension of data to be smaller than the number of instances, which is not suitable for high-dimensional data. For high-dimensional data analysis, the tensor-train decomposition is proved to be able to efficiently and effectively capture the spatial relations. Thus, we propose a tensor-train parameterization for ultra dimensionality reduction (TTPUDR) in which the traditional LPP mapping is tensorized in terms of tensor-trains and the LPP objective is replaced with the Frobenius norm to increase the robustness of the model. The manifold optimization technique is utilized to solve the new model. The performance of TTPUDR is assessed on classification problems and TTPUDR significantly outperforms the past methods and the several state-of-the-art methods.

Tensorial Recurrent Neural Networks for Longitudinal Data Analysis

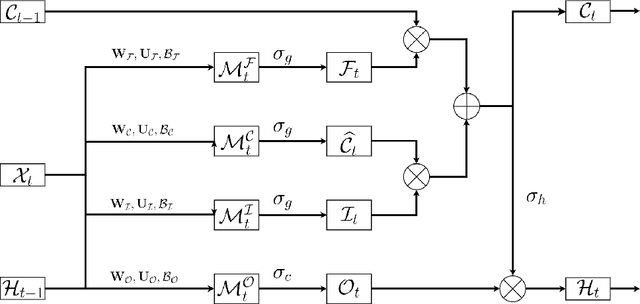
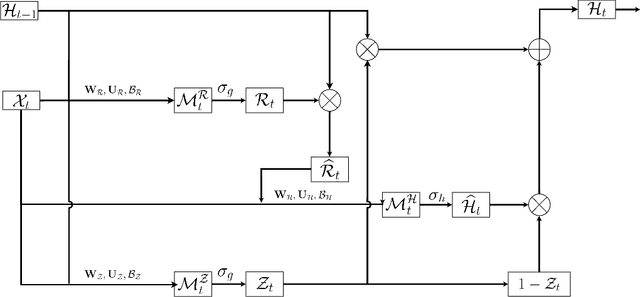
Traditional Recurrent Neural Networks assume vectorized data as inputs. However many data from modern science and technology come in certain structures such as tensorial time series data. To apply the recurrent neural networks for this type of data, a vectorisation process is necessary, while such a vectorisation leads to the loss of the precise information of the spatial or longitudinal dimensions. In addition, such a vectorized data is not an optimum solution for learning the representation of the longitudinal data. In this paper, we propose a new variant of tensorial neural networks which directly take tensorial time series data as inputs. We call this new variant as Tensorial Recurrent Neural Network (TRNN). The proposed TRNN is based on tensor Tucker decomposition.