Neural Ordinary Differential Equation Model for Evolutionary Subspace Clustering and Its Applications
Paper and Code
Jul 22, 2021
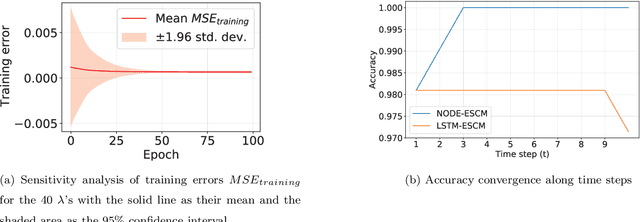
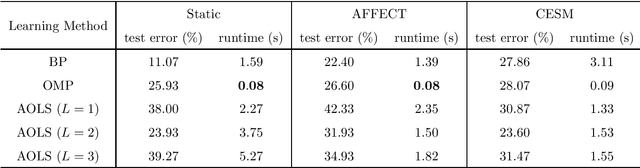
The neural ordinary differential equation (neural ODE) model has attracted increasing attention in time series analysis for its capability to process irregular time steps, i.e., data are not observed over equally-spaced time intervals. In multi-dimensional time series analysis, a task is to conduct evolutionary subspace clustering, aiming at clustering temporal data according to their evolving low-dimensional subspace structures. Many existing methods can only process time series with regular time steps while time series are unevenly sampled in many situations such as missing data. In this paper, we propose a neural ODE model for evolutionary subspace clustering to overcome this limitation and a new objective function with subspace self-expressiveness constraint is introduced. We demonstrate that this method can not only interpolate data at any time step for the evolutionary subspace clustering task, but also achieve higher accuracy than other state-of-the-art evolutionary subspace clustering methods. Both synthetic and real-world data are used to illustrate the efficacy of our proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge