Independent Component Analysis by Entropy Maximization with Kernels

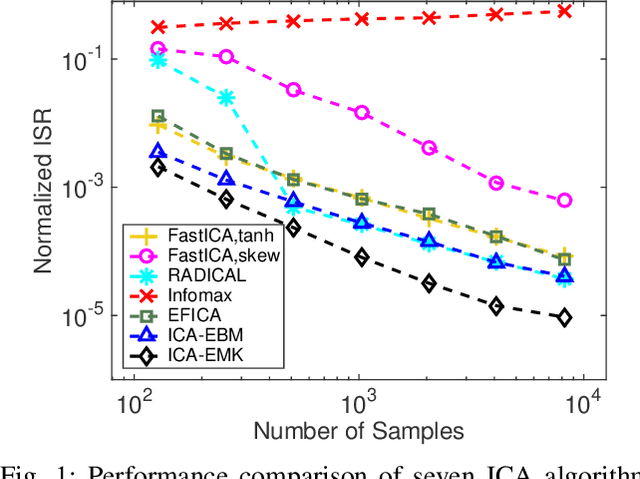
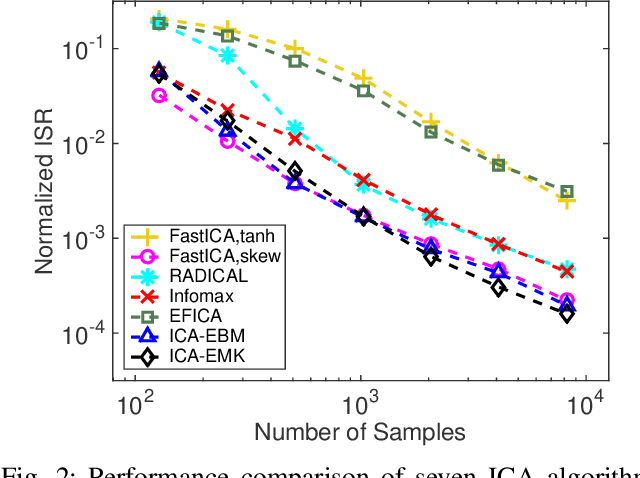
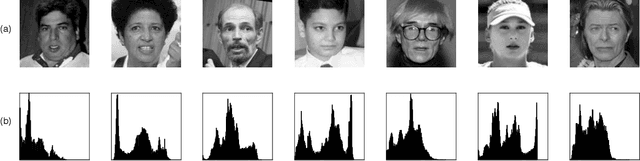
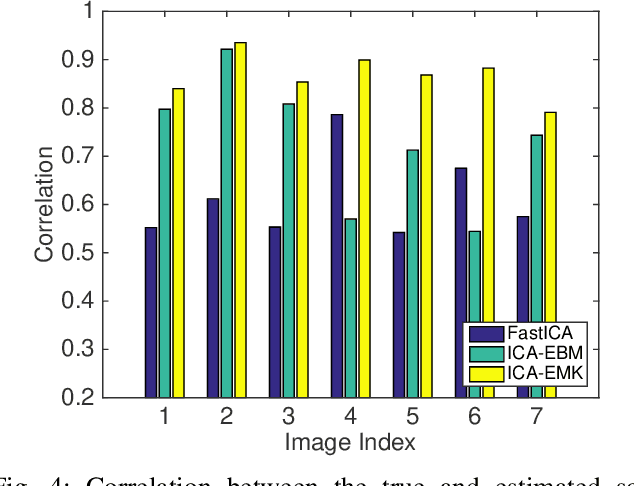
Independent component analysis (ICA) is the most popular method for blind source separation (BSS) with a diverse set of applications, such as biomedical signal processing, video and image analysis, and communications. Maximum likelihood (ML), an optimal theoretical framework for ICA, requires knowledge of the true underlying probability density function (PDF) of the latent sources, which, in many applications, is unknown. ICA algorithms cast in the ML framework often deviate from its theoretical optimality properties due to poor estimation of the source PDF. Therefore, accurate estimation of source PDFs is critical in order to avoid model mismatch and poor ICA performance. In this paper, we propose a new and efficient ICA algorithm based on entropy maximization with kernels, (ICA-EMK), which uses both global and local measuring functions as constraints to dynamically estimate the PDF of the sources with reasonable complexity. In addition, the new algorithm performs optimization with respect to each of the cost function gradient directions separately, enabling parallel implementations on multi-core computers. We demonstrate the superior performance of ICA-EMK over competing ICA algorithms using simulated as well as real-world data.

Independent Vector Analysis: Identification Conditions and Performance Bounds

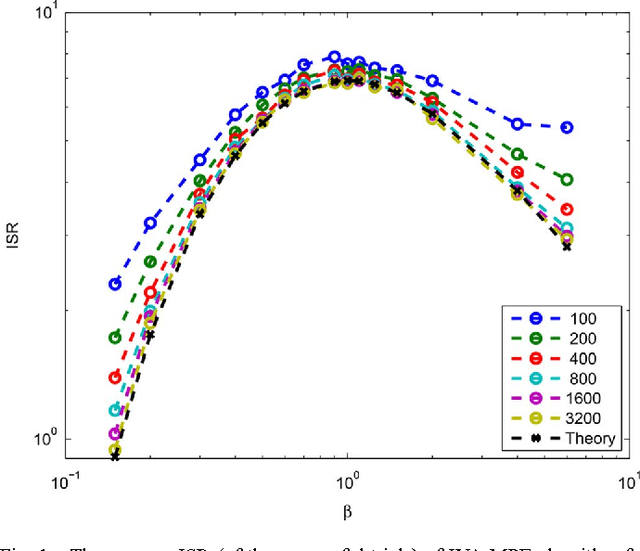
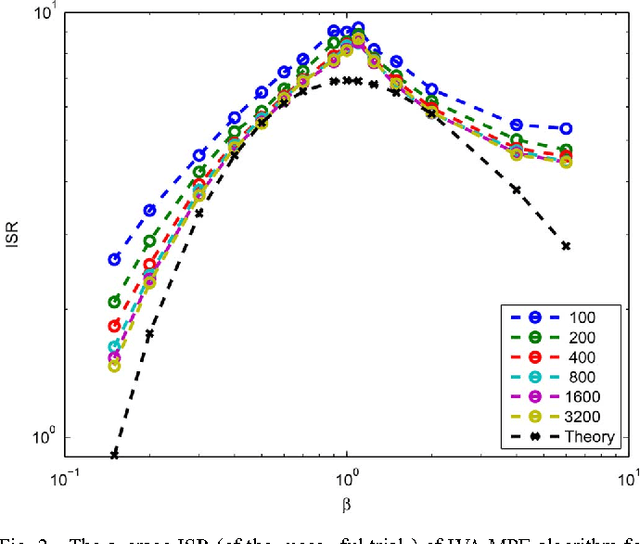
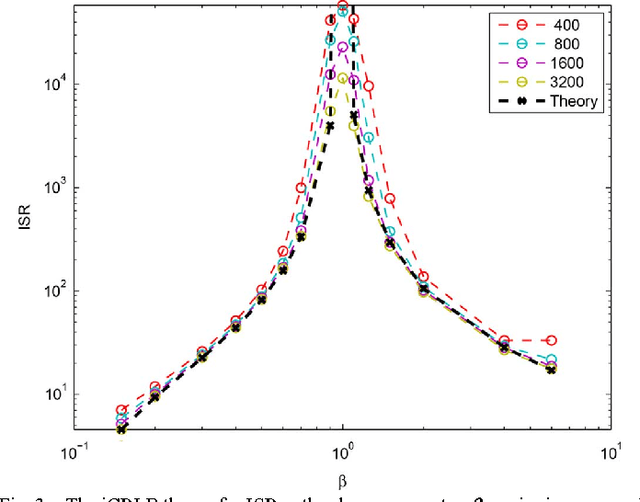
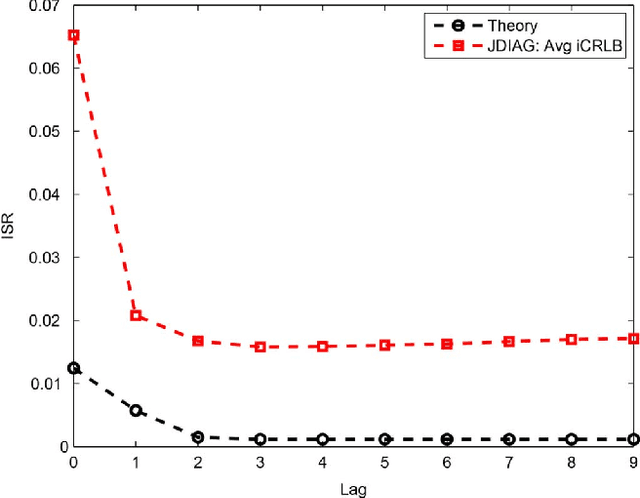
Recently, an extension of independent component analysis (ICA) from one to multiple datasets, termed independent vector analysis (IVA), has been the subject of significant research interest. IVA has also been shown to be a generalization of Hotelling's canonical correlation analysis. In this paper, we provide the identification conditions for a general IVA formulation, which accounts for linear, nonlinear, and sample-to-sample dependencies. The identification conditions are a generalization of previous results for ICA and for IVA when samples are independently and identically distributed. Furthermore, a principal aim of IVA is the identification of dependent sources between datasets. Thus, we provide the additional conditions for when the arbitrary ordering of the sources within each dataset is common. Performance bounds in terms of the Cramer-Rao lower bound are also provided for the demixing matrices and interference to source ratio. The performance of two IVA algorithms are compared to the theoretical bounds.