Independent Component Analysis by Entropy Maximization with Kernels
Paper and Code
Oct 22, 2016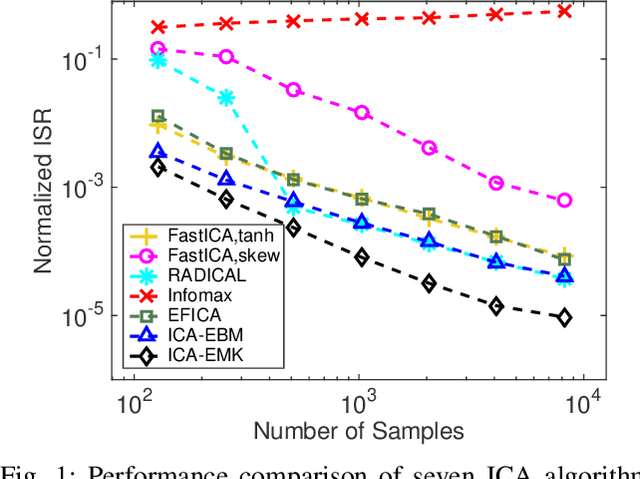
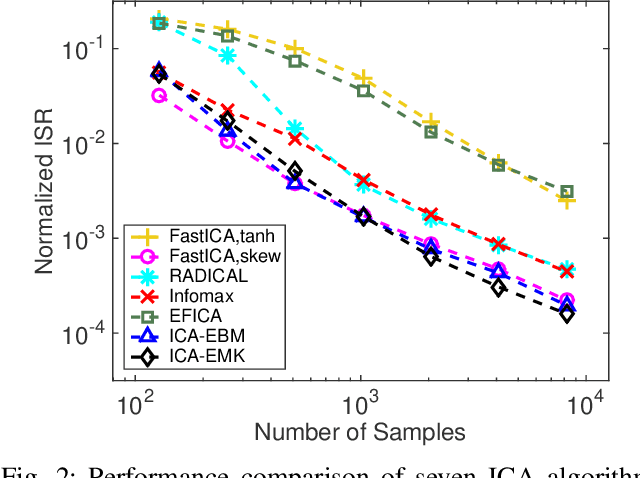
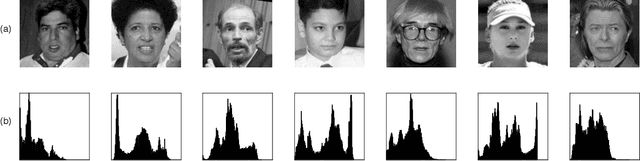
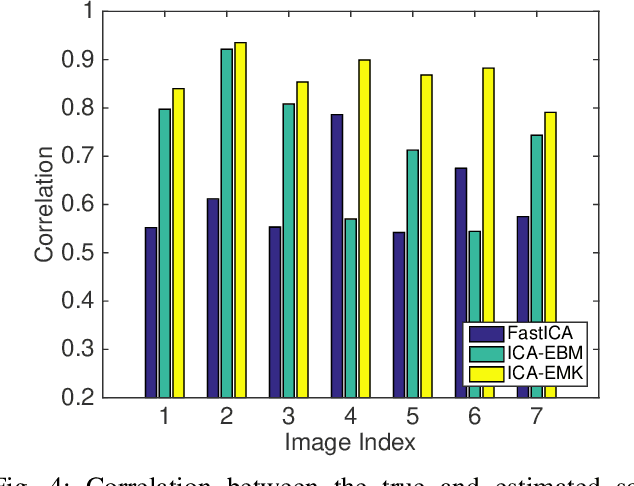
Independent component analysis (ICA) is the most popular method for blind source separation (BSS) with a diverse set of applications, such as biomedical signal processing, video and image analysis, and communications. Maximum likelihood (ML), an optimal theoretical framework for ICA, requires knowledge of the true underlying probability density function (PDF) of the latent sources, which, in many applications, is unknown. ICA algorithms cast in the ML framework often deviate from its theoretical optimality properties due to poor estimation of the source PDF. Therefore, accurate estimation of source PDFs is critical in order to avoid model mismatch and poor ICA performance. In this paper, we propose a new and efficient ICA algorithm based on entropy maximization with kernels, (ICA-EMK), which uses both global and local measuring functions as constraints to dynamically estimate the PDF of the sources with reasonable complexity. In addition, the new algorithm performs optimization with respect to each of the cost function gradient directions separately, enabling parallel implementations on multi-core computers. We demonstrate the superior performance of ICA-EMK over competing ICA algorithms using simulated as well as real-world data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge