Constrained Independent Vector Analysis with Reference for Multi-Subject fMRI Analysis

Independent component analysis (ICA) is now a widely used solution for the analysis of multi-subject functional magnetic resonance imaging (fMRI) data. Independent vector analysis (IVA) generalizes ICA to multiple datasets, i.e., to multi-subject data, and in addition to higher-order statistical information in ICA, it leverages the statistical dependence across the datasets as an additional type of statistical diversity. As such, it preserves variability in the estimation of single-subject maps but its performance might suffer when the number of datasets increases. Constrained IVA is an effective way to bypass computational issues and improve the quality of separation by incorporating available prior information. Existing constrained IVA approaches often rely on user-defined threshold values to define the constraints. However, an improperly selected threshold can have a negative impact on the final results. This paper proposes two novel methods for constrained IVA: one using an adaptive-reverse scheme to select variable thresholds for the constraints and a second one based on a threshold-free formulation by leveraging the unique structure of IVA. We demonstrate that our solutions provide an attractive solution to multi-subject fMRI analysis both by simulations and through analysis of resting state fMRI data collected from 98 subjects -- the highest number of subjects ever used by IVA algorithms. Our results show that both proposed approaches obtain significantly better separation quality and model match while providing computationally efficient and highly reproducible solutions.

New Interpretable Patterns and Discriminative Features from Brain Functional Network Connectivity Using Dictionary Learning

Independent component analysis (ICA) of multi-subject functional magnetic resonance imaging (fMRI) data has proven useful in providing a fully multivariate summary that can be used for multiple purposes. ICA can identify patterns that can discriminate between healthy controls (HC) and patients with various mental disorders such as schizophrenia (Sz). Temporal functional network connectivity (tFNC) obtained from ICA can effectively explain the interactions between brain networks. On the other hand, dictionary learning (DL) enables the discovery of hidden information in data using learnable basis signals through the use of sparsity. In this paper, we present a new method that leverages ICA and DL for the identification of directly interpretable patterns to discriminate between the HC and Sz groups. We use multi-subject resting-state fMRI data from $358$ subjects and form subject-specific tFNC feature vectors from ICA results. Then, we learn sparse representations of the tFNCs and introduce a new set of sparse features as well as new interpretable patterns from the learned atoms. Our experimental results show that the new representation not only leads to effective classification between HC and Sz groups using sparse features, but can also identify new interpretable patterns from the learned atoms that can help understand the complexities of mental diseases such as schizophrenia.

Multidataset Independent Subspace Analysis with Application to Multimodal Fusion

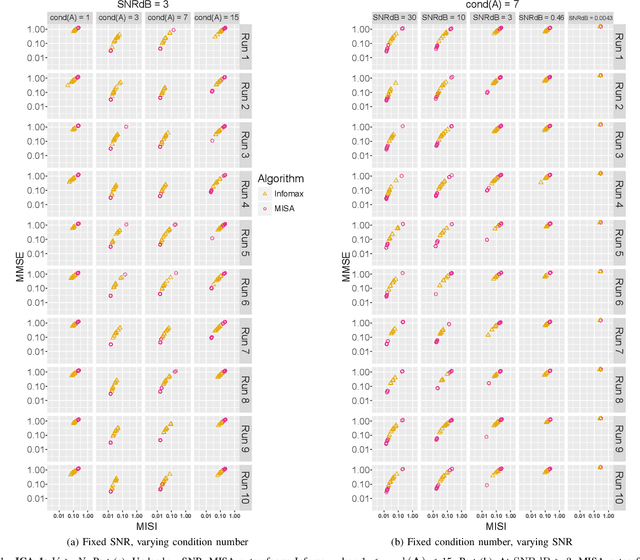
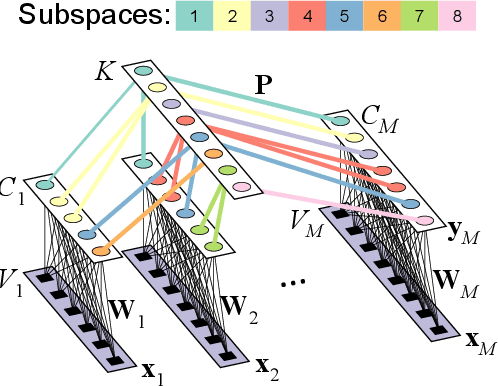
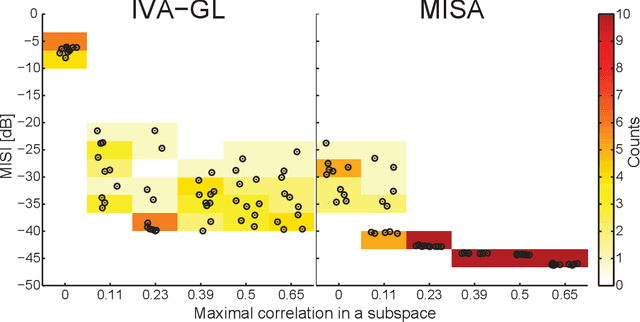
In the last two decades, unsupervised latent variable models---blind source separation (BSS) especially---have enjoyed a strong reputation for the interpretable features they produce. Seldom do these models combine the rich diversity of information available in multiple datasets. Multidatasets, on the other hand, yield joint solutions otherwise unavailable in isolation, with a potential for pivotal insights into complex systems. To take advantage of the complex multidimensional subspace structures that capture underlying modes of shared and unique variability across and within datasets, we present a direct, principled approach to multidataset combination. We design a new method called multidataset independent subspace analysis (MISA) that leverages joint information from multiple heterogeneous datasets in a flexible and synergistic fashion. Methodological innovations exploiting the Kotz distribution for subspace modeling in conjunction with a novel combinatorial optimization for evasion of local minima enable MISA to produce a robust generalization of independent component analysis (ICA), independent vector analysis (IVA), and independent subspace analysis (ISA) in a single unified model. We highlight the utility of MISA for multimodal information fusion, including sample-poor regimes and low signal-to-noise ratio scenarios, promoting novel applications in both unimodal and multimodal brain imaging data.

Independent Component Analysis by Entropy Maximization with Kernels

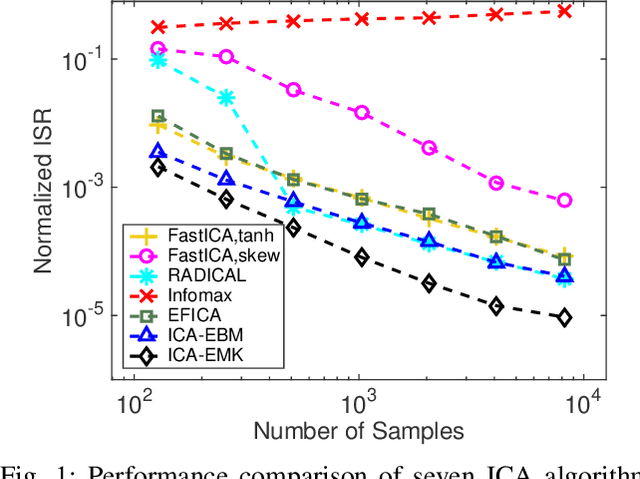
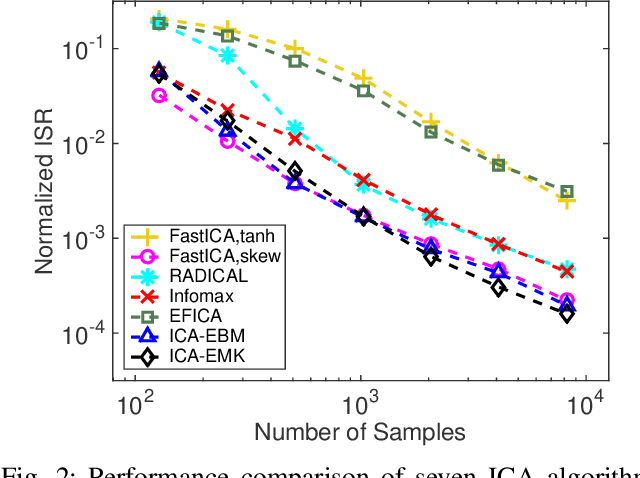
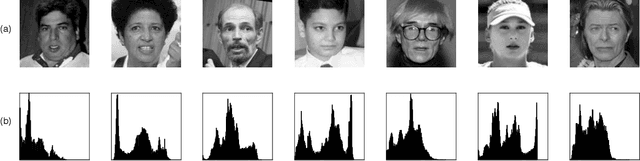
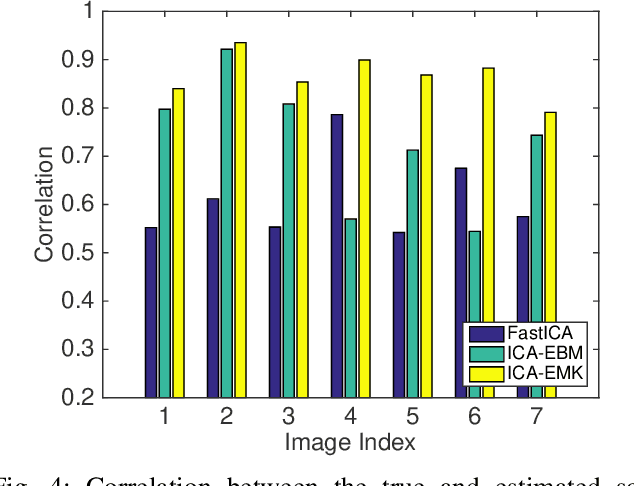
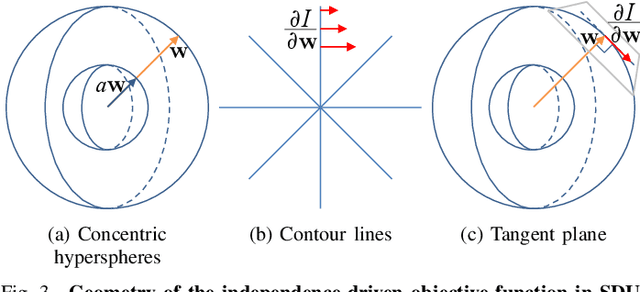
Independent component analysis (ICA) is the most popular method for blind source separation (BSS) with a diverse set of applications, such as biomedical signal processing, video and image analysis, and communications. Maximum likelihood (ML), an optimal theoretical framework for ICA, requires knowledge of the true underlying probability density function (PDF) of the latent sources, which, in many applications, is unknown. ICA algorithms cast in the ML framework often deviate from its theoretical optimality properties due to poor estimation of the source PDF. Therefore, accurate estimation of source PDFs is critical in order to avoid model mismatch and poor ICA performance. In this paper, we propose a new and efficient ICA algorithm based on entropy maximization with kernels, (ICA-EMK), which uses both global and local measuring functions as constraints to dynamically estimate the PDF of the sources with reasonable complexity. In addition, the new algorithm performs optimization with respect to each of the cost function gradient directions separately, enabling parallel implementations on multi-core computers. We demonstrate the superior performance of ICA-EMK over competing ICA algorithms using simulated as well as real-world data.

Enhancing ICA Performance by Exploiting Sparsity: Application to FMRI Analysis

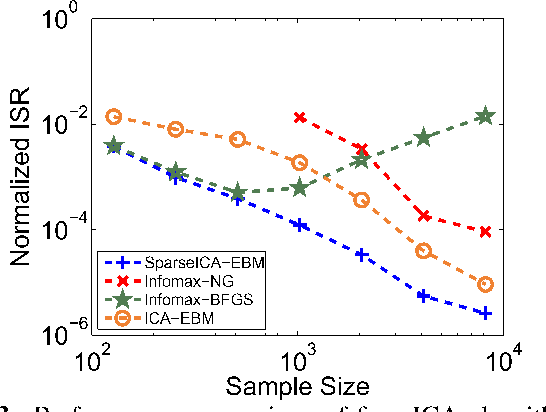
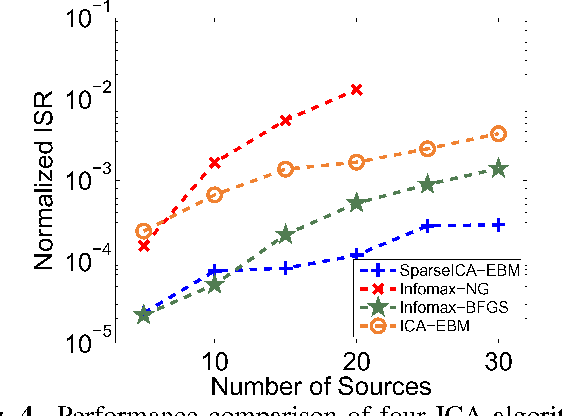
Independent component analysis (ICA) is a powerful method for blind source separation based on the assumption that sources are statistically independent. Though ICA has proven useful and has been employed in many applications, complete statistical independence can be too restrictive an assumption in practice. Additionally, important prior information about the data, such as sparsity, is usually available. Sparsity is a natural property of the data, a form of diversity, which, if incorporated into the ICA model, can relax the independence assumption, resulting in an improvement in the overall separation performance. In this work, we propose a new variant of ICA by entropy bound minimization (ICA-EBM)-a flexible, yet parameter-free algorithm-through the direct exploitation of sparsity. Using this new SparseICA-EBM algorithm, we study the synergy of independence and sparsity through simulations on synthetic as well as functional magnetic resonance imaging (fMRI)-like data.