Enhancing ICA Performance by Exploiting Sparsity: Application to FMRI Analysis
Paper and Code
Oct 19, 2016

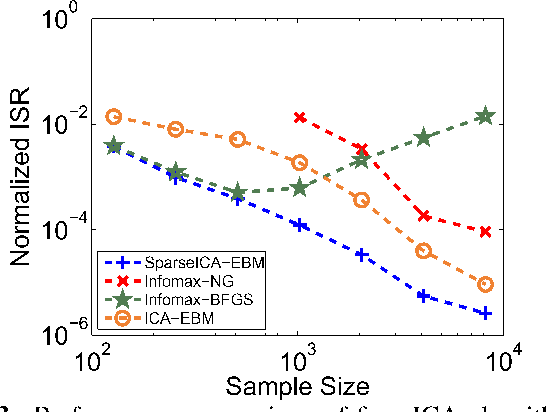
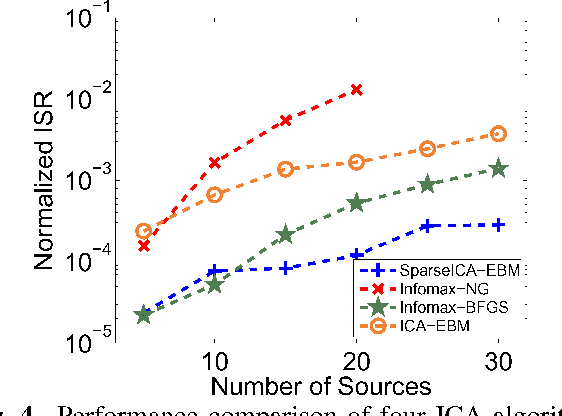
Independent component analysis (ICA) is a powerful method for blind source separation based on the assumption that sources are statistically independent. Though ICA has proven useful and has been employed in many applications, complete statistical independence can be too restrictive an assumption in practice. Additionally, important prior information about the data, such as sparsity, is usually available. Sparsity is a natural property of the data, a form of diversity, which, if incorporated into the ICA model, can relax the independence assumption, resulting in an improvement in the overall separation performance. In this work, we propose a new variant of ICA by entropy bound minimization (ICA-EBM)-a flexible, yet parameter-free algorithm-through the direct exploitation of sparsity. Using this new SparseICA-EBM algorithm, we study the synergy of independence and sparsity through simulations on synthetic as well as functional magnetic resonance imaging (fMRI)-like data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge