Constrained Independent Vector Analysis with Reference for Multi-Subject fMRI Analysis

Independent component analysis (ICA) is now a widely used solution for the analysis of multi-subject functional magnetic resonance imaging (fMRI) data. Independent vector analysis (IVA) generalizes ICA to multiple datasets, i.e., to multi-subject data, and in addition to higher-order statistical information in ICA, it leverages the statistical dependence across the datasets as an additional type of statistical diversity. As such, it preserves variability in the estimation of single-subject maps but its performance might suffer when the number of datasets increases. Constrained IVA is an effective way to bypass computational issues and improve the quality of separation by incorporating available prior information. Existing constrained IVA approaches often rely on user-defined threshold values to define the constraints. However, an improperly selected threshold can have a negative impact on the final results. This paper proposes two novel methods for constrained IVA: one using an adaptive-reverse scheme to select variable thresholds for the constraints and a second one based on a threshold-free formulation by leveraging the unique structure of IVA. We demonstrate that our solutions provide an attractive solution to multi-subject fMRI analysis both by simulations and through analysis of resting state fMRI data collected from 98 subjects -- the highest number of subjects ever used by IVA algorithms. Our results show that both proposed approaches obtain significantly better separation quality and model match while providing computationally efficient and highly reproducible solutions.

Better Generalization with Semantic IDs: A case study in Ranking for Recommendations

Training good representations for items is critical in recommender models. Typically, an item is assigned a unique randomly generated ID, and is commonly represented by learning an embedding corresponding to the value of the random ID. Although widely used, this approach have limitations when the number of items are large and items are power-law distributed -- typical characteristics of real-world recommendation systems. This leads to the item cold-start problem, where the model is unable to make reliable inferences for tail and previously unseen items. Removing these ID features and their learned embeddings altogether to combat cold-start issue severely degrades the recommendation quality. Content-based item embeddings are more reliable, but they are expensive to store and use, particularly for users' past item interaction sequence. In this paper, we use Semantic IDs, a compact discrete item representations learned from content embeddings using RQ-VAE that captures hierarchy of concepts in items. We showcase how we use them as a replacement of item IDs in a resource-constrained ranking model used in an industrial-scale video sharing platform. Moreover, we show how Semantic IDs improves the generalization ability of our system, without sacrificing top-level metrics.

Recommender Systems with Generative Retrieval

Modern recommender systems leverage large-scale retrieval models consisting of two stages: training a dual-encoder model to embed queries and candidates in the same space, followed by an Approximate Nearest Neighbor (ANN) search to select top candidates given a query's embedding. In this paper, we propose a new single-stage paradigm: a generative retrieval model which autoregressively decodes the identifiers for the target candidates in one phase. To do this, instead of assigning randomly generated atomic IDs to each item, we generate Semantic IDs: a semantically meaningful tuple of codewords for each item that serves as its unique identifier. We use a hierarchical method called RQ-VAE to generate these codewords. Once we have the Semantic IDs for all the items, a Transformer based sequence-to-sequence model is trained to predict the Semantic ID of the next item. Since this model predicts the tuple of codewords identifying the next item directly in an autoregressive manner, it can be considered a generative retrieval model. We show that our recommender system trained in this new paradigm improves the results achieved by current SOTA models on the Amazon dataset. Moreover, we demonstrate that the sequence-to-sequence model coupled with hierarchical Semantic IDs offers better generalization and hence improves retrieval of cold-start items for recommendations.

On Local Linear Convergence of Projected Gradient Descent for Unit-Modulus Least Squares

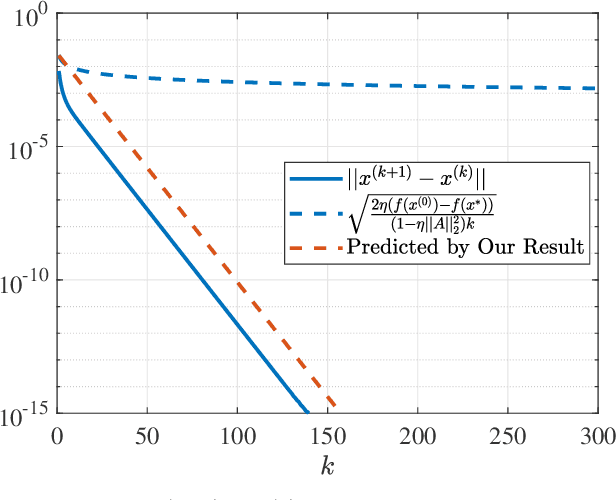
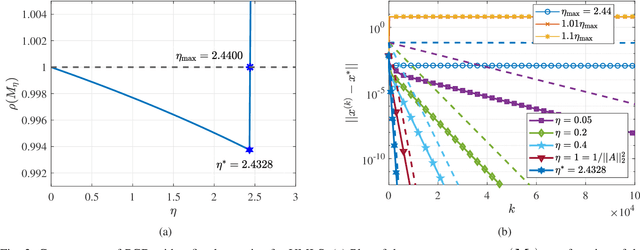
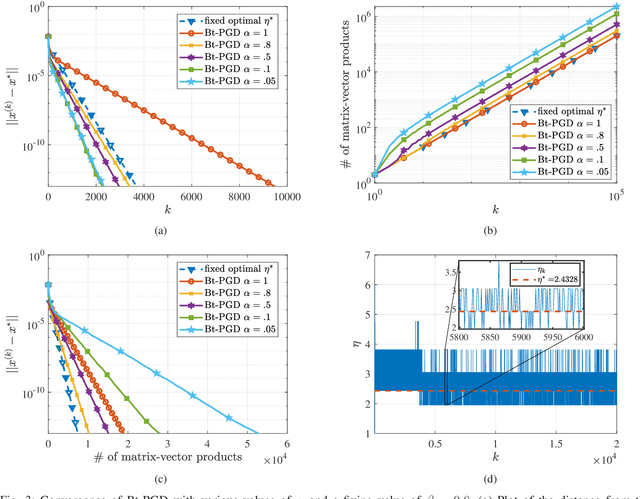
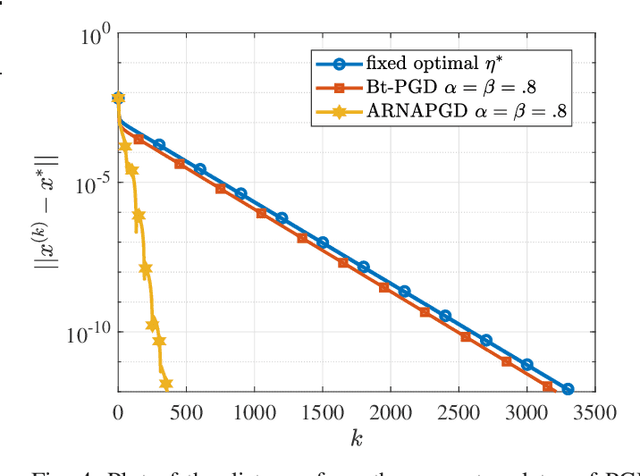
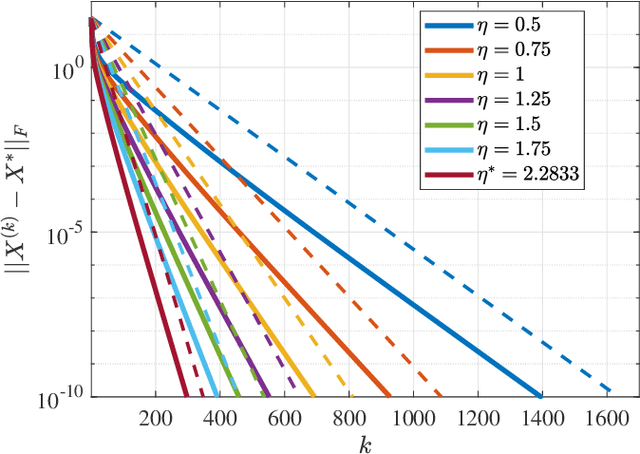
The unit-modulus least squares (UMLS) problem has a wide spectrum of applications in signal processing, e.g., phase-only beamforming, phase retrieval, radar code design, and sensor network localization. Scalable first-order methods such as projected gradient descent (PGD) have recently been studied as a simple yet efficient approach to solving the UMLS problem. Existing results on the convergence of PGD for UMLS often focus on global convergence to stationary points. As a non-convex problem, only a sublinear convergence rate has been established. However, these results do not explain the fast convergence of PGD frequently observed in practice. This manuscript presents a novel analysis of convergence of PGD for UMLS, justifying the linear convergence behavior of the algorithm near the solution. By exploiting the local structure of the objective function and the constraint set, we establish an exact expression for the convergence rate and characterize the conditions for linear convergence. Simulations show that our theoretical analysis corroborates numerical examples. Furthermore, variants of PGD with adaptive step sizes are proposed based on the new insight revealed in our convergence analysis. The variants show substantial acceleration in practice.

On Asymptotic Linear Convergence of Projected Gradient Descent for Constrained Least Squares

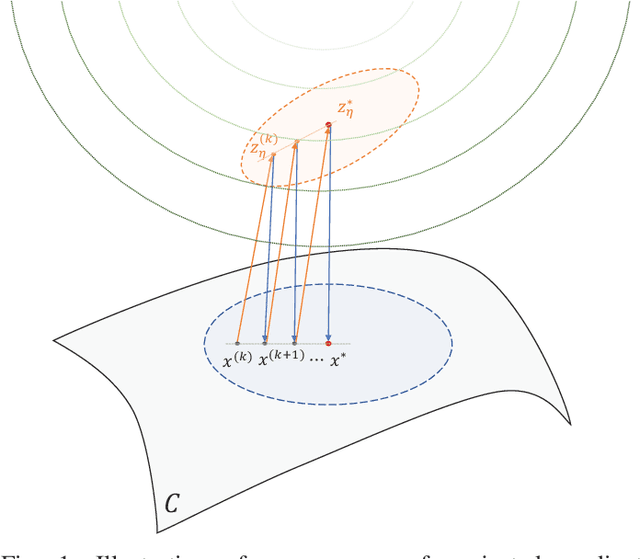
Many recent problems in signal processing and machine learning such as compressed sensing, image restoration, matrix/tensor recovery, and non-negative matrix factorization can be cast as constrained optimization. Projected gradient descent is a simple yet efficient method for solving such constrained optimization problems. Local convergence analysis furthers our understanding of its asymptotic behavior near the solution, offering sharper bounds on the convergence rate compared to global convergence analysis. However, local guarantees often appear scattered in problem-specific areas of machine learning and signal processing. This manuscript presents a unified framework for the local convergence analysis of projected gradient descent in the context of constrained least squares. The proposed analysis offers insights into pivotal local convergence properties such as the condition of linear convergence, the region of convergence, the exact asymptotic rate of convergence, and the bound on the number of iterations needed to reach a certain level of accuracy. To demonstrate the applicability of the proposed approach, we present a recipe for the convergence analysis of PGD and demonstrate it via a beginning-to-end application of the recipe on four fundamental problems, namely, linearly constrained least squares, sparse recovery, least squares with the unit norm constraint, and matrix completion.

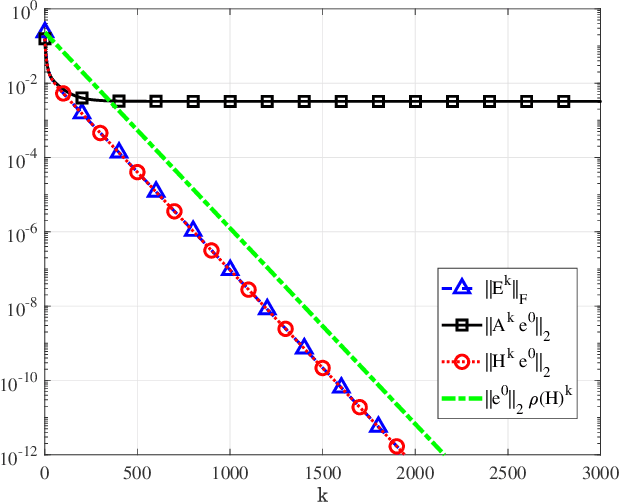
Exact Linear Convergence Rate Analysis for Low-Rank Symmetric Matrix Completion via Gradient Descent

Factorization-based gradient descent is a scalable and efficient algorithm for solving low-rank matrix completion. Recent progress in structured non-convex optimization has offered global convergence guarantees for gradient descent under certain statistical assumptions on the low-rank matrix and the sampling set. However, while the theory suggests gradient descent enjoys fast linear convergence to a global solution of the problem, the universal nature of the bounding technique prevents it from obtaining an accurate estimate of the rate of convergence. In this paper, we perform a local analysis of the exact linear convergence rate of gradient descent for factorization-based matrix completion for symmetric matrices. Without any additional assumptions on the underlying model, we identify the deterministic condition for local convergence of gradient descent, which only depends on the solution matrix and the sampling set. More crucially, our analysis provides a closed-form expression of the asymptotic rate of convergence that matches exactly with the linear convergence observed in practice. To the best of our knowledge, our result is the first one that offers the exact rate of convergence of gradient descent for matrix factorization in Euclidean space for matrix completion.

Parkinson's Disease Digital Biomarker Discovery with Optimized Transitions and Inferred Markov Emissions

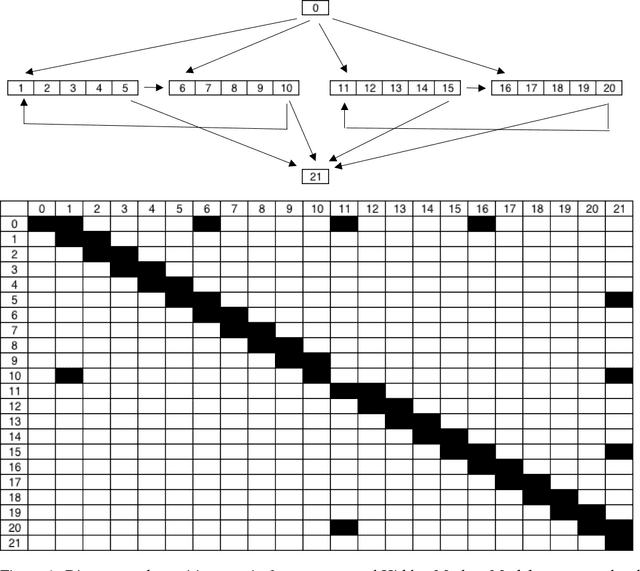
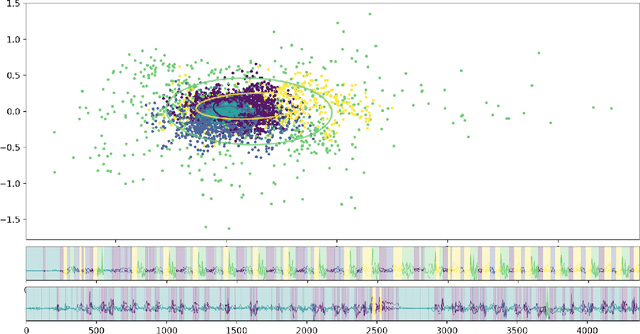
We search for digital biomarkers from Parkinson's Disease by observing approximate repetitive patterns matching hypothesized step and stride periodic cycles. These observations were modeled as a cycle of hidden states with randomness allowing deviation from a canonical pattern of transitions and emissions, under the hypothesis that the averaged features of hidden states would serve to informatively characterize classes of patients/controls. We propose a Hidden Semi-Markov Model (HSMM), a latent-state model, emitting 3D-acceleration vectors. Transitions and emissions are inferred from data. We fit separate models per unique device and training label. Hidden Markov Models (HMM) force geometric distributions of the duration spent at each state before transition to a new state. Instead, our HSMM allows us to specify the distribution of state duration. This modified version is more effective because we are interested more in each state's duration than the sequence of distinct states, allowing inclusion of these durations the feature vector.