Exact Linear Convergence Rate Analysis for Low-Rank Symmetric Matrix Completion via Gradient Descent
Paper and Code
Feb 06, 2021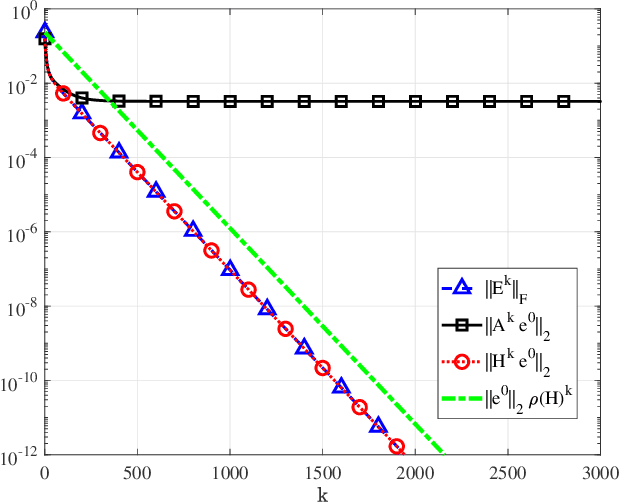
Factorization-based gradient descent is a scalable and efficient algorithm for solving low-rank matrix completion. Recent progress in structured non-convex optimization has offered global convergence guarantees for gradient descent under certain statistical assumptions on the low-rank matrix and the sampling set. However, while the theory suggests gradient descent enjoys fast linear convergence to a global solution of the problem, the universal nature of the bounding technique prevents it from obtaining an accurate estimate of the rate of convergence. In this paper, we perform a local analysis of the exact linear convergence rate of gradient descent for factorization-based matrix completion for symmetric matrices. Without any additional assumptions on the underlying model, we identify the deterministic condition for local convergence of gradient descent, which only depends on the solution matrix and the sampling set. More crucially, our analysis provides a closed-form expression of the asymptotic rate of convergence that matches exactly with the linear convergence observed in practice. To the best of our knowledge, our result is the first one that offers the exact rate of convergence of gradient descent for matrix factorization in Euclidean space for matrix completion.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge