Identifiable Solutions to Foreground Signature Extraction from Hyperspectral Images in an Intimate Mixing Scenario

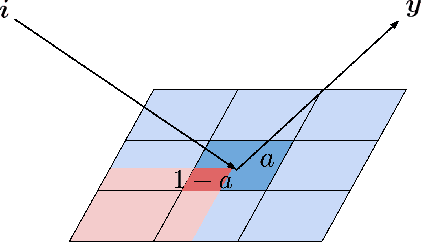
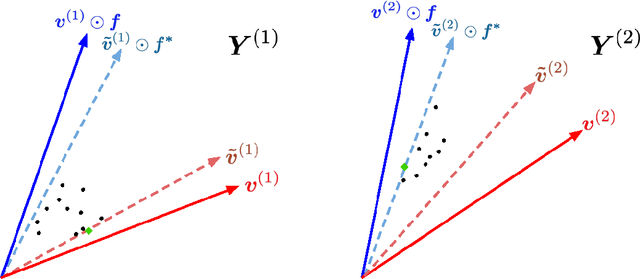
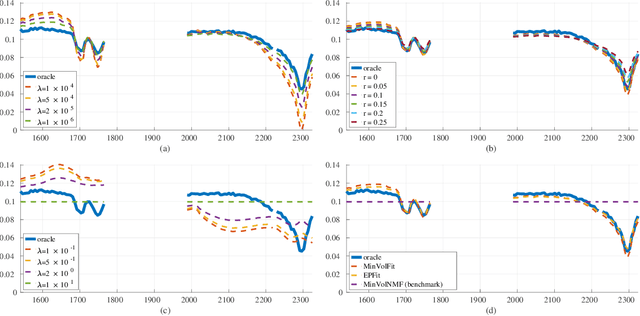
The problem of foreground material signature extraction in an intimate (nonlinear) mixing setting is considered. It is possible for a foreground material signature to appear in combination with multiple background material signatures. We explore a framework for foreground material signature extraction based on a patch model that accounts for such background variation. We identify data conditions under which a foreground material signature can be extracted up to scaling and elementwise-inverse variations. We present algorithms based on volume minimization and endpoint member identification to recover foreground material signatures under these conditions. Numerical experiments on real and synthetic data illustrate the efficacy of the proposed algorithms.

On Local Linear Convergence of Projected Gradient Descent for Unit-Modulus Least Squares

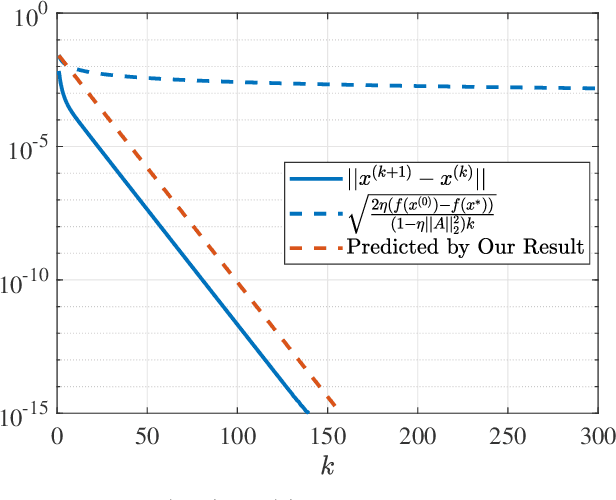
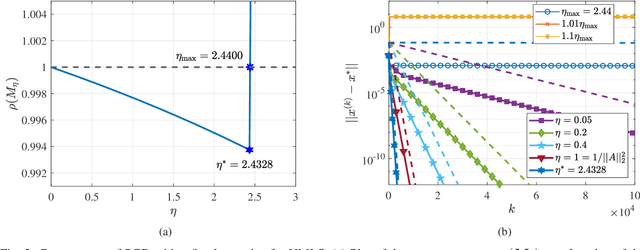
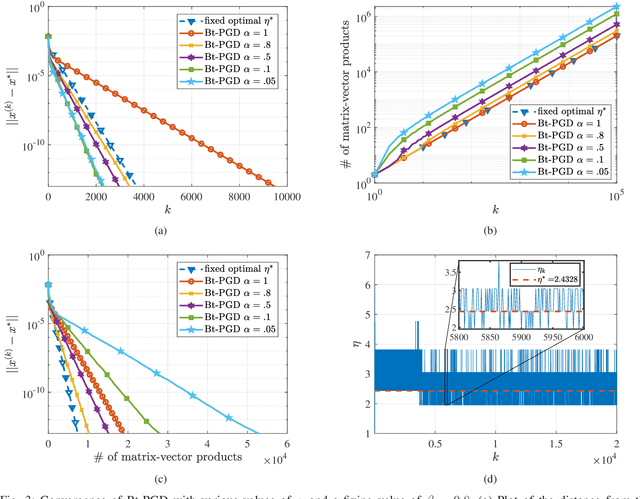
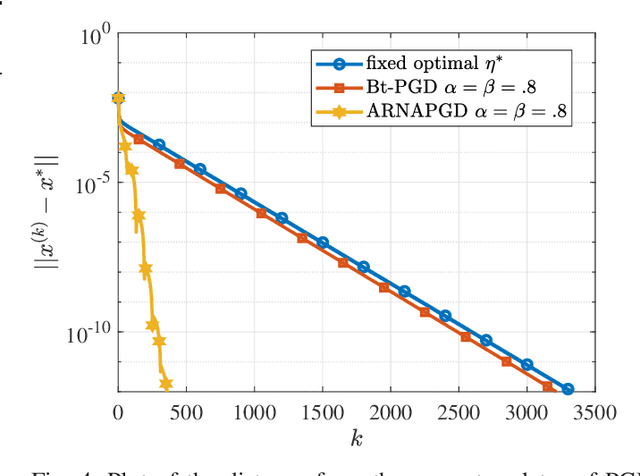
The unit-modulus least squares (UMLS) problem has a wide spectrum of applications in signal processing, e.g., phase-only beamforming, phase retrieval, radar code design, and sensor network localization. Scalable first-order methods such as projected gradient descent (PGD) have recently been studied as a simple yet efficient approach to solving the UMLS problem. Existing results on the convergence of PGD for UMLS often focus on global convergence to stationary points. As a non-convex problem, only a sublinear convergence rate has been established. However, these results do not explain the fast convergence of PGD frequently observed in practice. This manuscript presents a novel analysis of convergence of PGD for UMLS, justifying the linear convergence behavior of the algorithm near the solution. By exploiting the local structure of the objective function and the constraint set, we establish an exact expression for the convergence rate and characterize the conditions for linear convergence. Simulations show that our theoretical analysis corroborates numerical examples. Furthermore, variants of PGD with adaptive step sizes are proposed based on the new insight revealed in our convergence analysis. The variants show substantial acceleration in practice.

On Asymptotic Linear Convergence of Projected Gradient Descent for Constrained Least Squares

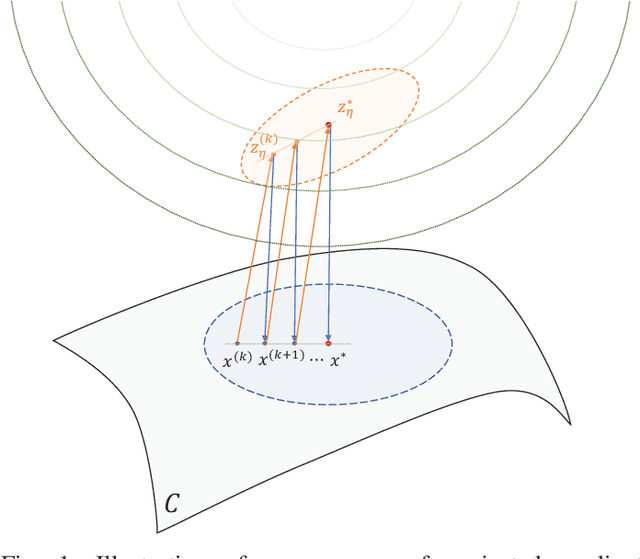
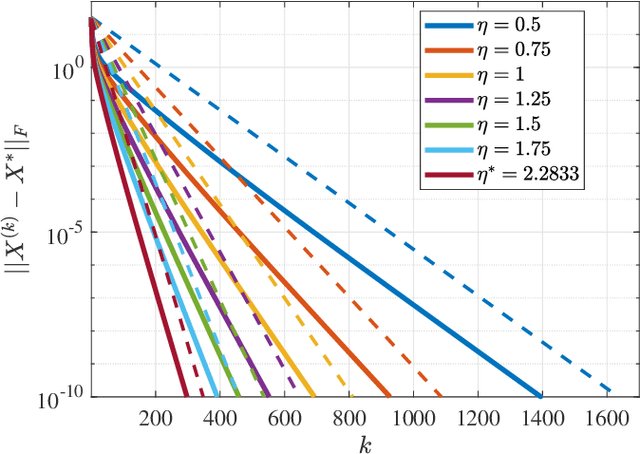
Many recent problems in signal processing and machine learning such as compressed sensing, image restoration, matrix/tensor recovery, and non-negative matrix factorization can be cast as constrained optimization. Projected gradient descent is a simple yet efficient method for solving such constrained optimization problems. Local convergence analysis furthers our understanding of its asymptotic behavior near the solution, offering sharper bounds on the convergence rate compared to global convergence analysis. However, local guarantees often appear scattered in problem-specific areas of machine learning and signal processing. This manuscript presents a unified framework for the local convergence analysis of projected gradient descent in the context of constrained least squares. The proposed analysis offers insights into pivotal local convergence properties such as the condition of linear convergence, the region of convergence, the exact asymptotic rate of convergence, and the bound on the number of iterations needed to reach a certain level of accuracy. To demonstrate the applicability of the proposed approach, we present a recipe for the convergence analysis of PGD and demonstrate it via a beginning-to-end application of the recipe on four fundamental problems, namely, linearly constrained least squares, sparse recovery, least squares with the unit norm constraint, and matrix completion.

Active Learning in Incomplete Label Multiple Instance Multiple Label Learning

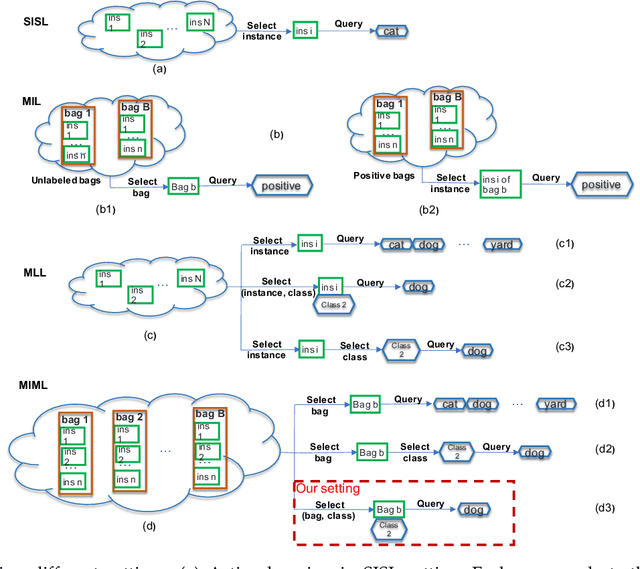
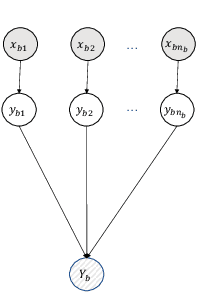
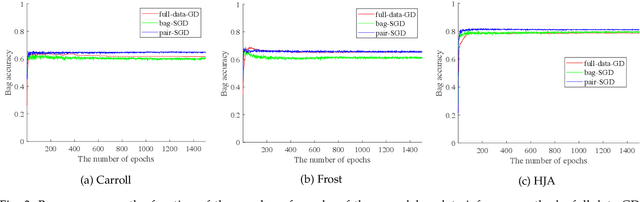
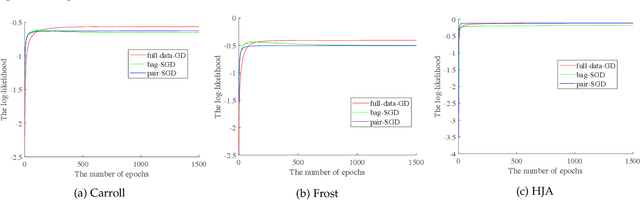
In multiple instance multiple label learning, each sample, a bag, consists of multiple instances. To alleviate labeling complexity, each sample is associated with a set of bag-level labels leaving instances within the bag unlabeled. This setting is more convenient and natural for representing complicated objects, which have multiple semantic meanings. Compared to single instance labeling, this approach allows for labeling larger datasets at an equivalent labeling cost. However, for sufficiently large datasets, labeling all bags may become prohibitively costly. Active learning uses an iterative labeling and retraining approach aiming to provide reasonable classification performance using a small number of labeled samples. To our knowledge, only a few works in the area of active learning in the MIML setting are available. These approaches can provide practical solutions to reduce labeling cost but their efficacy remains unclear. In this paper, we propose a novel bag-class pair based approach for active learning in the MIML setting. Due to the partial availability of bag-level labels, we focus on the incomplete-label MIML setting for the proposed active learning approach. Our approach is based on a discriminative graphical model with efficient and exact inference. For the query process, we adapt active learning criteria to the novel bag-class pair selection strategy. Additionally, we introduce an online stochastic gradient descent algorithm to provide an efficient model update after each query. Numerical experiments on benchmark datasets illustrate the robustness of the proposed approach.

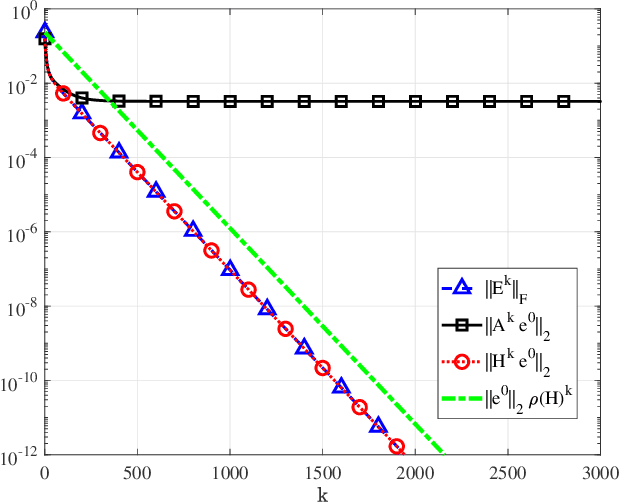
Exact Linear Convergence Rate Analysis for Low-Rank Symmetric Matrix Completion via Gradient Descent

Factorization-based gradient descent is a scalable and efficient algorithm for solving low-rank matrix completion. Recent progress in structured non-convex optimization has offered global convergence guarantees for gradient descent under certain statistical assumptions on the low-rank matrix and the sampling set. However, while the theory suggests gradient descent enjoys fast linear convergence to a global solution of the problem, the universal nature of the bounding technique prevents it from obtaining an accurate estimate of the rate of convergence. In this paper, we perform a local analysis of the exact linear convergence rate of gradient descent for factorization-based matrix completion for symmetric matrices. Without any additional assumptions on the underlying model, we identify the deterministic condition for local convergence of gradient descent, which only depends on the solution matrix and the sampling set. More crucially, our analysis provides a closed-form expression of the asymptotic rate of convergence that matches exactly with the linear convergence observed in practice. To the best of our knowledge, our result is the first one that offers the exact rate of convergence of gradient descent for matrix factorization in Euclidean space for matrix completion.

Weakly-supervised Dictionary Learning

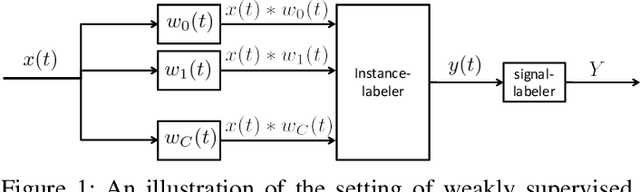
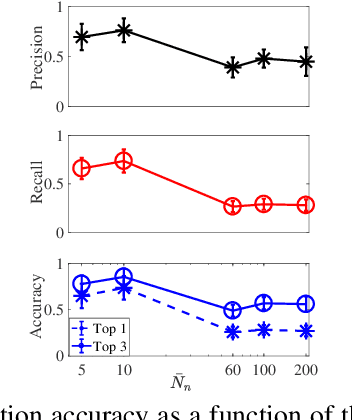
We present a probabilistic modeling and inference framework for discriminative analysis dictionary learning under a weak supervision setting. Dictionary learning approaches have been widely used for tasks such as low-level signal denoising and restoration as well as high-level classification tasks, which can be applied to audio and image analysis. Synthesis dictionary learning aims at jointly learning a dictionary and corresponding sparse coefficients to provide accurate data representation. This approach is useful for denoising and signal restoration, but may lead to sub-optimal classification performance. By contrast, analysis dictionary learning provides a transform that maps data to a sparse discriminative representation suitable for classification. We consider the problem of analysis dictionary learning for time-series data under a weak supervision setting in which signals are assigned with a global label instead of an instantaneous label signal. We propose a discriminative probabilistic model that incorporates both label information and sparsity constraints on the underlying latent instantaneous label signal using cardinality control. We present the expectation maximization (EM) procedure for maximum likelihood estimation (MLE) of the proposed model. To facilitate a computationally efficient E-step, we propose both a chain and a novel tree graph reformulation of the graphical model. The performance of the proposed model is demonstrated on both synthetic and real-world data.

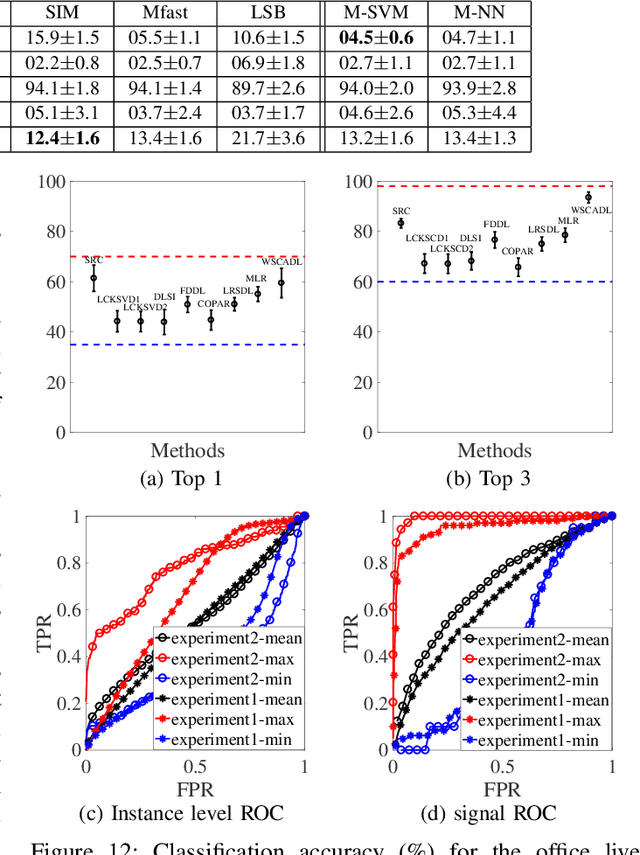
Confidence-Constrained Maximum Entropy Framework for Learning from Multi-Instance Data

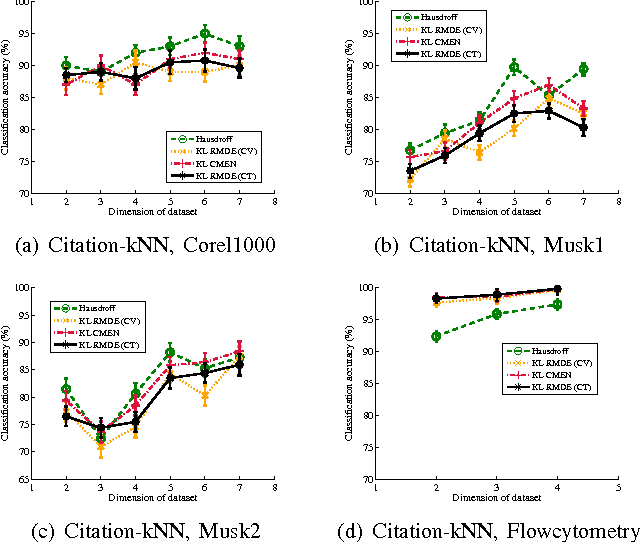
Multi-instance data, in which each object (bag) contains a collection of instances, are widespread in machine learning, computer vision, bioinformatics, signal processing, and social sciences. We present a maximum entropy (ME) framework for learning from multi-instance data. In this approach each bag is represented as a distribution using the principle of ME. We introduce the concept of confidence-constrained ME (CME) to simultaneously learn the structure of distribution space and infer each distribution. The shared structure underlying each density is used to learn from instances inside each bag. The proposed CME is free of tuning parameters. We devise a fast optimization algorithm capable of handling large scale multi-instance data. In the experimental section, we evaluate the performance of the proposed approach in terms of exact rank recovery in the space of distributions and compare it with the regularized ME approach. Moreover, we compare the performance of CME with Multi-Instance Learning (MIL) state-of-the-art algorithms and show a comparable performance in terms of accuracy with reduced computational complexity.

Dynamic Programming for Instance Annotation in Multi-instance Multi-label Learning

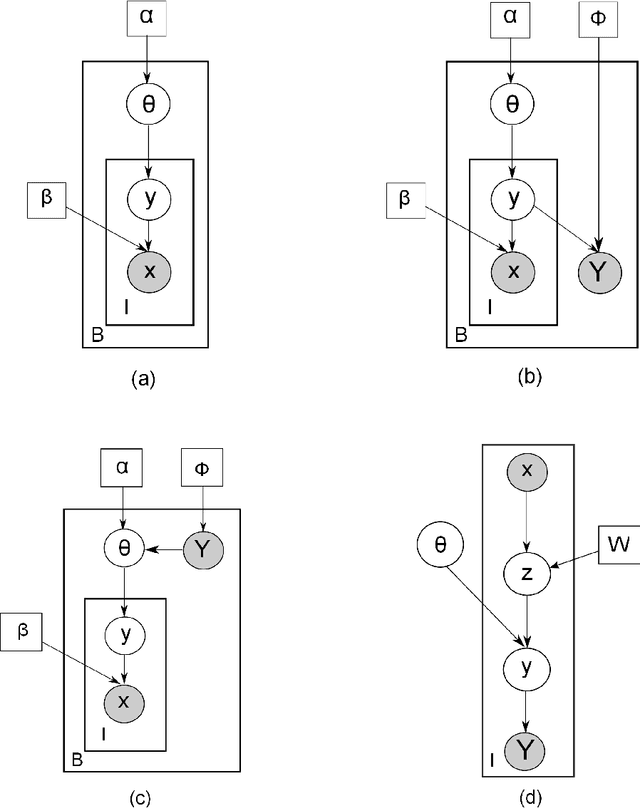
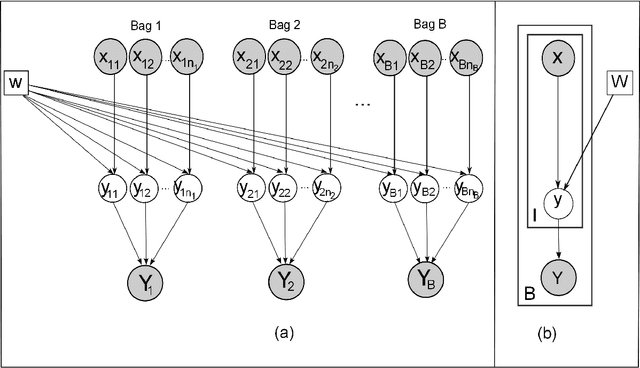
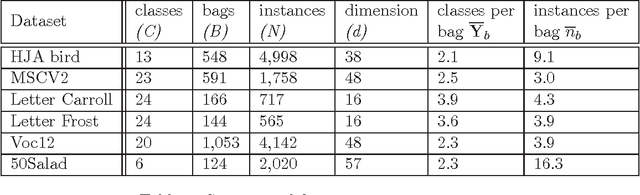
Labeling data for classification requires significant human effort. To reduce labeling cost, instead of labeling every instance, a group of instances (bag) is labeled by a single bag label. Computer algorithms are then used to infer the label for each instance in a bag, a process referred to as instance annotation. This task is challenging due to the ambiguity regarding the instance labels. We propose a discriminative probabilistic model for the instance annotation problem and introduce an expectation maximization framework for inference, based on the maximum likelihood approach. For many probabilistic approaches, brute-force computation of the instance label posterior probability given its bag label is exponential in the number of instances in the bag. Our key contribution is a dynamic programming method for computing the posterior that is linear in the number of instances. We evaluate our methods using both benchmark and real world data sets, in the domain of bird song, image annotation, and activity recognition. In many cases, the proposed framework outperforms, sometimes significantly, the current state-of-the-art MIML learning methods, both in instance label prediction and bag label prediction.

Novelty Detection Under Multi-Instance Multi-Label Framework

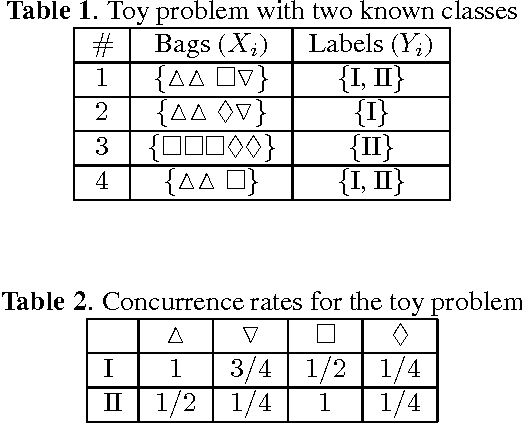
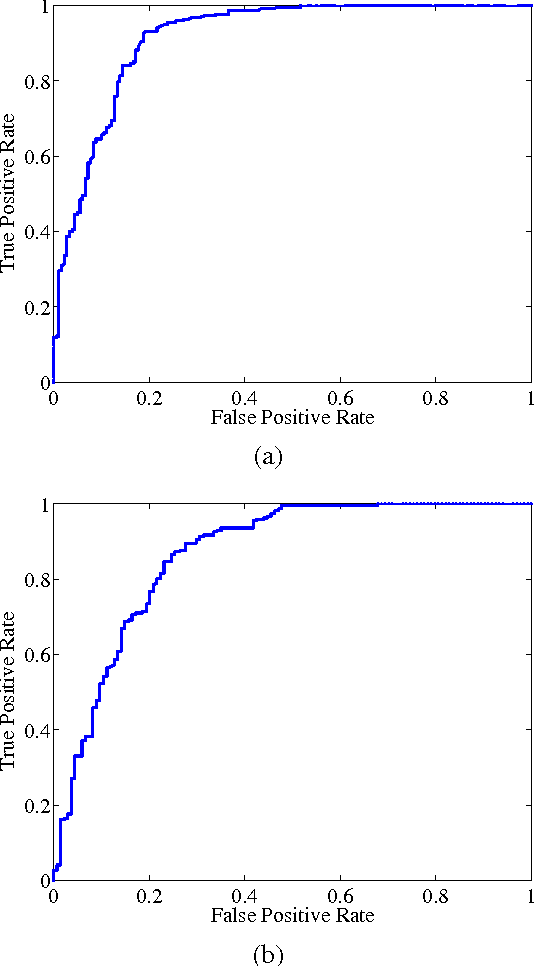
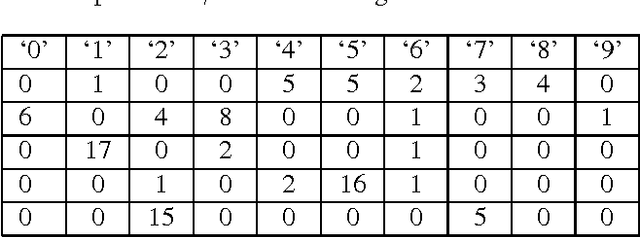
Novelty detection plays an important role in machine learning and signal processing. This paper studies novelty detection in a new setting where the data object is represented as a bag of instances and associated with multiple class labels, referred to as multi-instance multi-label (MIML) learning. Contrary to the common assumption in MIML that each instance in a bag belongs to one of the known classes, in novelty detection, we focus on the scenario where bags may contain novel-class instances. The goal is to determine, for any given instance in a new bag, whether it belongs to a known class or a novel class. Detecting novelty in the MIML setting captures many real-world phenomena and has many potential applications. For example, in a collection of tagged images, the tag may only cover a subset of objects existing in the images. Discovering an object whose class has not been previously tagged can be useful for the purpose of soliciting a label for the new object class. To address this novel problem, we present a discriminative framework for detecting new class instances. Experiments demonstrate the effectiveness of our proposed method, and reveal that the presence of unlabeled novel instances in training bags is helpful to the detection of such instances in testing stage.

Empirical estimation of entropy functionals with confidence

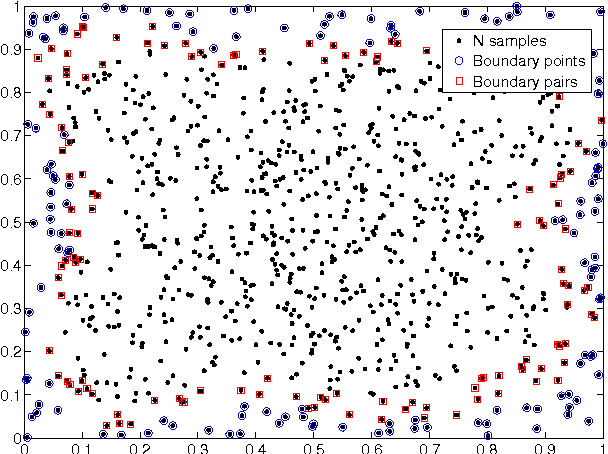
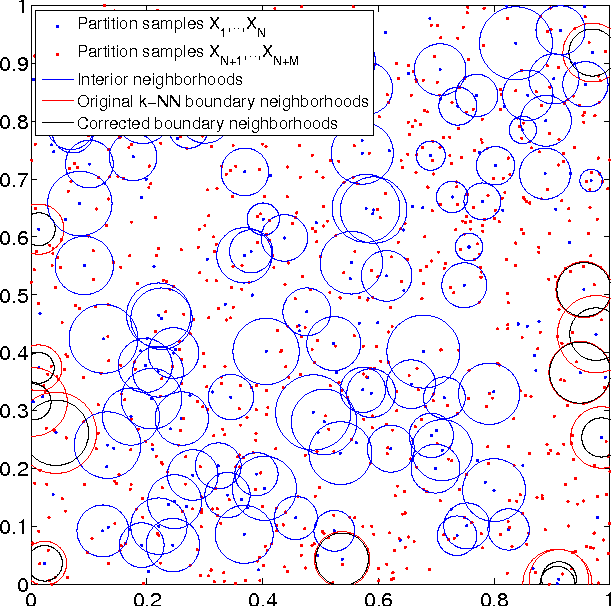
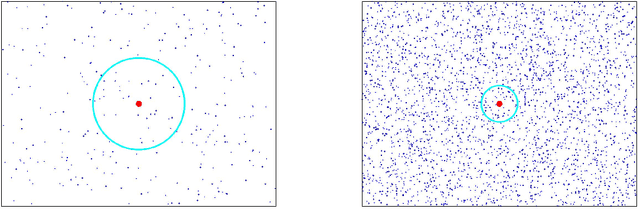
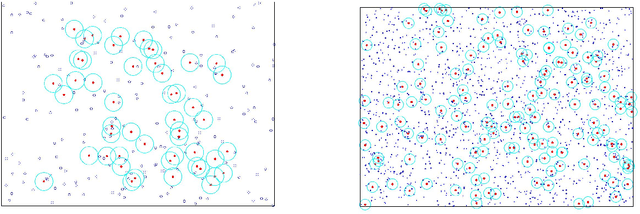
This paper introduces a class of k-nearest neighbor ($k$-NN) estimators called bipartite plug-in (BPI) estimators for estimating integrals of non-linear functions of a probability density, such as Shannon entropy and R\'enyi entropy. The density is assumed to be smooth, have bounded support, and be uniformly bounded from below on this set. Unlike previous $k$-NN estimators of non-linear density functionals, the proposed estimator uses data-splitting and boundary correction to achieve lower mean square error. Specifically, we assume that $T$ i.i.d. samples ${X}_i \in \mathbb{R}^d$ from the density are split into two pieces of cardinality $M$ and $N$ respectively, with $M$ samples used for computing a k-nearest-neighbor density estimate and the remaining $N$ samples used for empirical estimation of the integral of the density functional. By studying the statistical properties of k-NN balls, explicit rates for the bias and variance of the BPI estimator are derived in terms of the sample size, the dimension of the samples and the underlying probability distribution. Based on these results, it is possible to specify optimal choice of tuning parameters $M/T$, $k$ for maximizing the rate of decrease of the mean square error (MSE). The resultant optimized BPI estimator converges faster and achieves lower mean squared error than previous $k$-NN entropy estimators. In addition, a central limit theorem is established for the BPI estimator that allows us to specify tight asymptotic confidence intervals.