High-Dimensional Sequential Change Detection

We address the problem of detecting a change in the distribution of a high-dimensional multivariate normal time series. Assuming that the post-change parameters are unknown and estimated using a window of historical data, we extend the framework of quickest change detection (QCD) to the highdimensional setting in which the number of variables increases proportionally with the size of the window used to estimate the post-change parameters. Our analysis reveals that an information theoretic quantity, which we call the Normalized High- Dimensional Kullback-Leibler divergence (NHDKL), governs the high-dimensional asymptotic performance of QCD procedures. Specifically, we show that the detection delay is asymptotically inversely proportional to the difference between the NHDKL of the true post-change versus pre-change distributions and the NHDKL of the true versus estimated post-change distributions. In cases of perfect estimation, where the latter NHDKL is zero, the delay is inversely proportional to the NHDKL between the post-change and pre-change distributions alone. Thus, our analysis is a direct generalization of the traditional fixed-dimension, large-sample asymptotic framework, where the standard KL divergence is asymptotically inversely proportional to detection delay. Finally, we identify parameter estimators that asymptotically minimize the NHDKL between the true versus estimated post-change distributions, resulting in a QCD method that is guaranteed to outperform standard approaches based on fixed-dimension asymptotics.

Universal Training of Neural Networks to Achieve Bayes Optimal Classification Accuracy

This work invokes the notion of $f$-divergence to introduce a novel upper bound on the Bayes error rate of a general classification task. We show that the proposed bound can be computed by sampling from the output of a parameterized model. Using this practical interpretation, we introduce the Bayes optimal learning threshold (BOLT) loss whose minimization enforces a classification model to achieve the Bayes error rate. We validate the proposed loss for image and text classification tasks, considering MNIST, Fashion-MNIST, CIFAR-10, and IMDb datasets. Numerical experiments demonstrate that models trained with BOLT achieve performance on par with or exceeding that of cross-entropy, particularly on challenging datasets. This highlights the potential of BOLT in improving generalization.

Community Detection in High-Dimensional Graph Ensembles

Detecting communities in high-dimensional graphs can be achieved by applying random matrix theory where the adjacency matrix of the graph is modeled by a Stochastic Block Model (SBM). However, the SBM makes an unrealistic assumption that the edge probabilities are homogeneous within communities, i.e., the edges occur with the same probabilities. The Degree-Corrected SBM is a generalization of the SBM that allows these edge probabilities to be different, but existing results from random matrix theory are not directly applicable to this heterogeneous model. In this paper, we derive a transformation of the adjacency matrix that eliminates this heterogeneity and preserves the relevant eigenstructure for community detection. We propose a test based on the extreme eigenvalues of this transformed matrix and (1) provide a method for controlling the significance level, (2) formulate a conjecture that the test achieves power one for all positive significance levels in the limit as the number of nodes approaches infinity, and (3) provide empirical evidence and theory supporting these claims.

Iterative Sketching for Secure Coded Regression

In this work, we propose methods for speeding up linear regression distributively, while ensuring security. We leverage randomized sketching techniques, and improve straggler resilience in asynchronous systems. Specifically, we apply a random orthonormal matrix and then subsample \textit{blocks}, to simultaneously secure the information and reduce the dimension of the regression problem. In our setup, the transformation corresponds to an encoded encryption in an \textit{approximate gradient coding scheme}, and the subsampling corresponds to the responses of the non-straggling workers; in a centralized coded computing network. This results in a distributive \textit{iterative sketching} approach for an $\ell_2$-subspace embedding, \textit{i.e.} a new sketch is considered at each iteration. We also focus on the special case of the \textit{Subsampled Randomized Hadamard Transform}, which we generalize to block sampling; and discuss how it can be modified in order to secure the data.

Graph Sparsification by Approximate Matrix Multiplication

Graphs arising in statistical problems, signal processing, large networks, combinatorial optimization, and data analysis are often dense, which causes both computational and storage bottlenecks. One way of \textit{sparsifying} a \textit{weighted} graph, while sharing the same vertices as the original graph but reducing the number of edges, is through \textit{spectral sparsification}. We study this problem through the perspective of RandNLA. Specifically, we utilize randomized matrix multiplication to give a clean and simple analysis of how sampling according to edge weights gives a spectral approximation to graph Laplacians. Through the $CR$-MM algorithm, we attain a simple and computationally efficient sparsifier whose resulting Laplacian estimate is unbiased and of minimum variance. Furthermore, we define a new notion of \textit{additive spectral sparsifiers}, which has not been considered in the literature.

SOLBP: Second-Order Loopy Belief Propagation for Inference in Uncertain Bayesian Networks

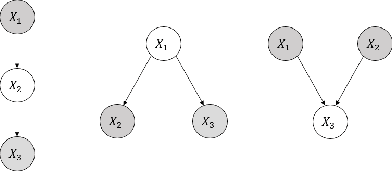
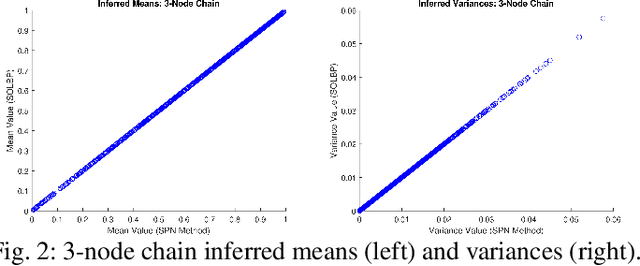
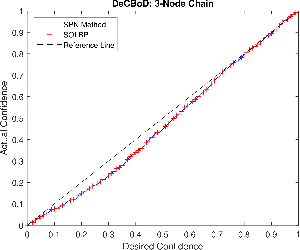
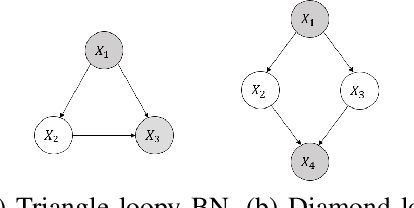
In second-order uncertain Bayesian networks, the conditional probabilities are only known within distributions, i.e., probabilities over probabilities. The delta-method has been applied to extend exact first-order inference methods to propagate both means and variances through sum-product networks derived from Bayesian networks, thereby characterizing epistemic uncertainty, or the uncertainty in the model itself. Alternatively, second-order belief propagation has been demonstrated for polytrees but not for general directed acyclic graph structures. In this work, we extend Loopy Belief Propagation to the setting of second-order Bayesian networks, giving rise to Second-Order Loopy Belief Propagation (SOLBP). For second-order Bayesian networks, SOLBP generates inferences consistent with those generated by sum-product networks, while being more computationally efficient and scalable.

Uncertain Bayesian Networks: Learning from Incomplete Data

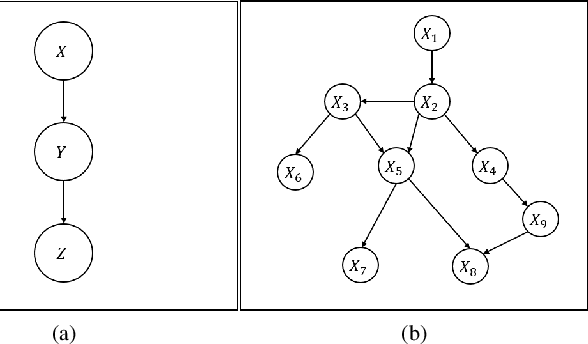
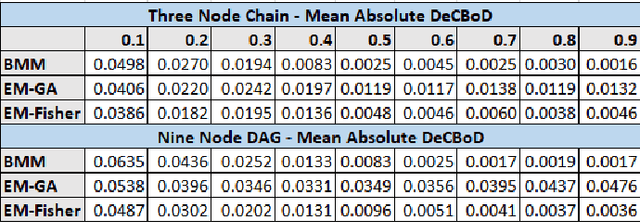
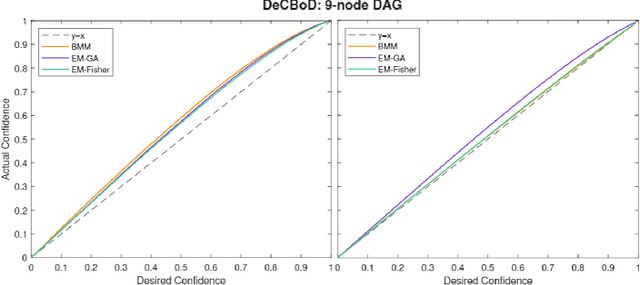
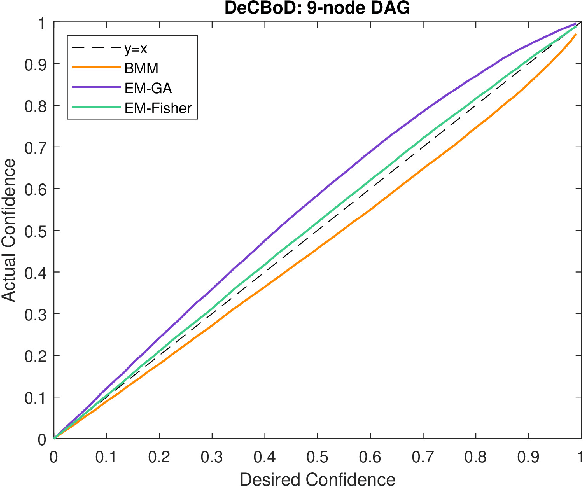
When the historical data are limited, the conditional probabilities associated with the nodes of Bayesian networks are uncertain and can be empirically estimated. Second order estimation methods provide a framework for both estimating the probabilities and quantifying the uncertainty in these estimates. We refer to these cases as uncer tain or second-order Bayesian networks. When such data are complete, i.e., all variable values are observed for each instantiation, the conditional probabilities are known to be Dirichlet-distributed. This paper improves the current state-of-the-art approaches for handling uncertain Bayesian networks by enabling them to learn distributions for their parameters, i.e., conditional probabilities, with incomplete data. We extensively evaluate various methods to learn the posterior of the parameters through the desired and empirically derived strength of confidence bounds for various queries.

High dimensional stochastic linear contextual bandit with missing covariates

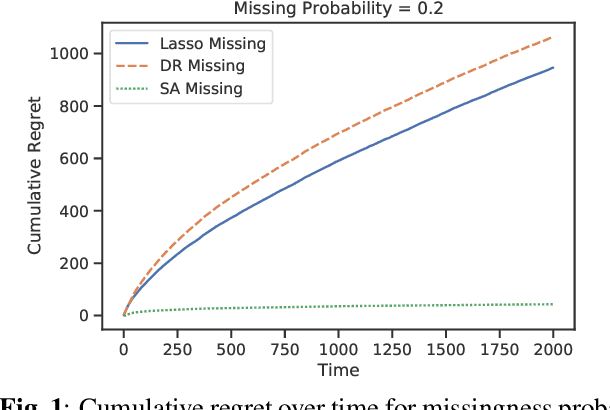
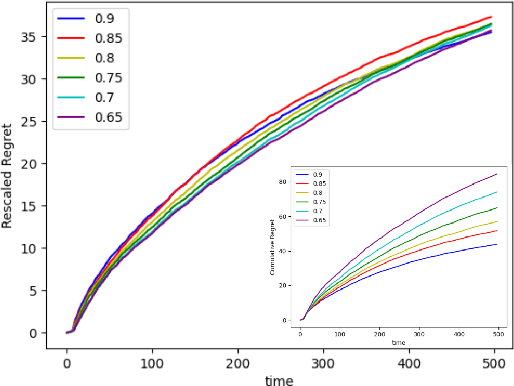
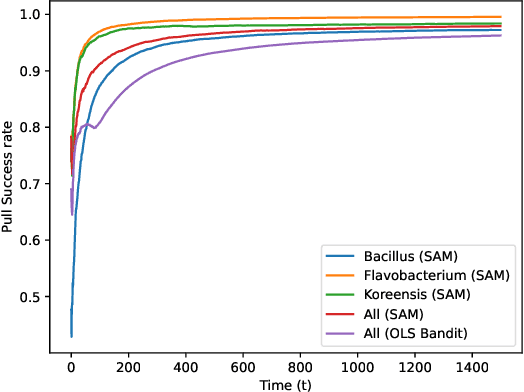
Recent works in bandit problems adopted lasso convergence theory in the sequential decision-making setting. Even with fully observed contexts, there are technical challenges that hinder the application of existing lasso convergence theory: 1) proving the restricted eigenvalue condition under conditionally sub-Gaussian noise and 2) accounting for the dependence between the context variables and the chosen actions. This paper studies the effect of missing covariates on regret for stochastic linear bandit algorithms. Our work provides a high-probability upper bound on the regret incurred by the proposed algorithm in terms of covariate sampling probabilities, showing that the regret degrades due to missingness by at most $\zeta_{min}^2$, where $\zeta_{min}$ is the minimum probability of observing covariates in the context vector. We illustrate our algorithm for the practical application of experimental design for collecting gene expression data by a sequential selection of class discriminating DNA probes.

Orthonormal Sketches for Secure Coded Regression}

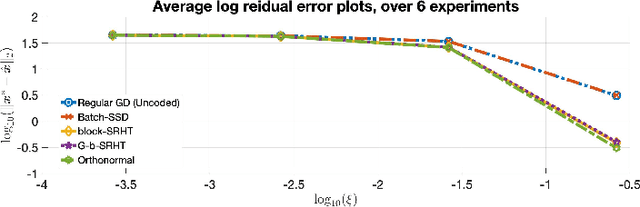
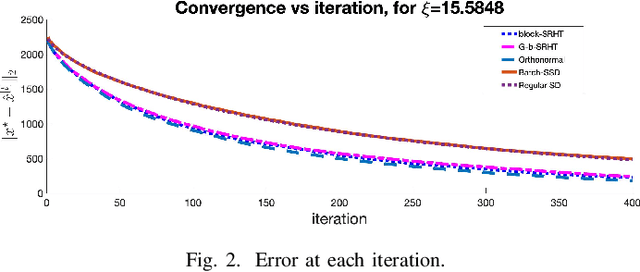
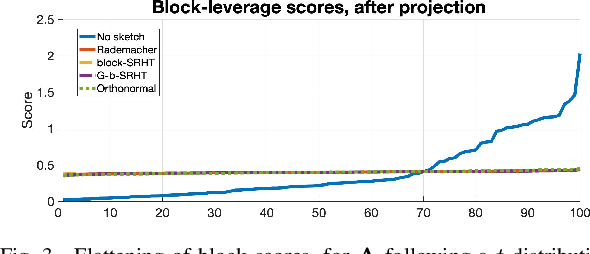
In this work, we propose a method for speeding up linear regression distributively, while ensuring security. We leverage randomized sketching techniques, and improve straggler resilience in asynchronous systems. Specifically, we apply a random orthonormal matrix and then subsample in \textit{blocks}, to simultaneously secure the information and reduce the dimension of the regression problem. In our setup, the transformation corresponds to an encoded encryption in an \textit{approximate} gradient coding scheme, and the subsampling corresponds to the responses of the non-straggling workers; in a centralized coded computing network. We focus on the special case of the \textit{Subsampled Randomized Hadamard Transform}, which we generalize to block sampling; and discuss how it can be used to secure the data. We illustrate the performance through numerical experiments.

Data Discovery Using Lossless Compression-Based Sparse Representation

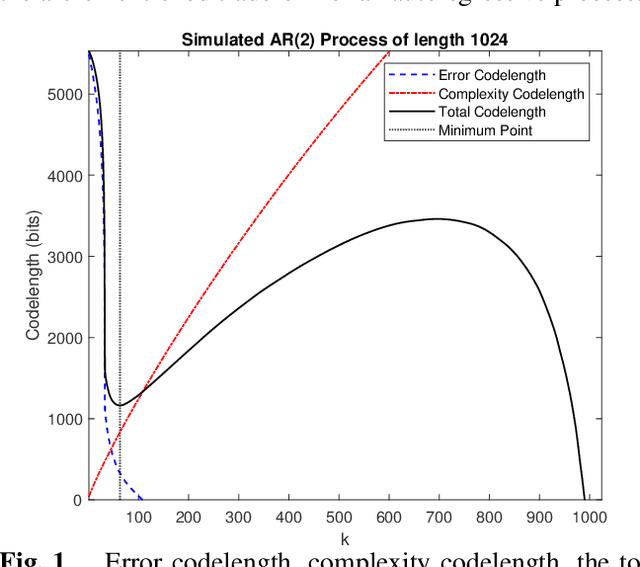
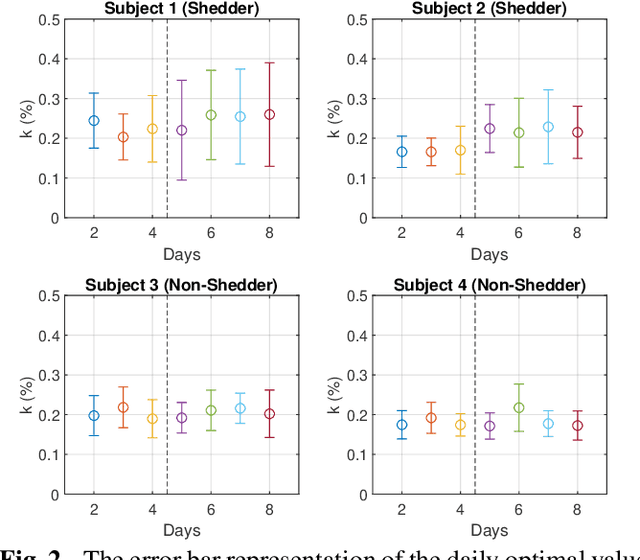
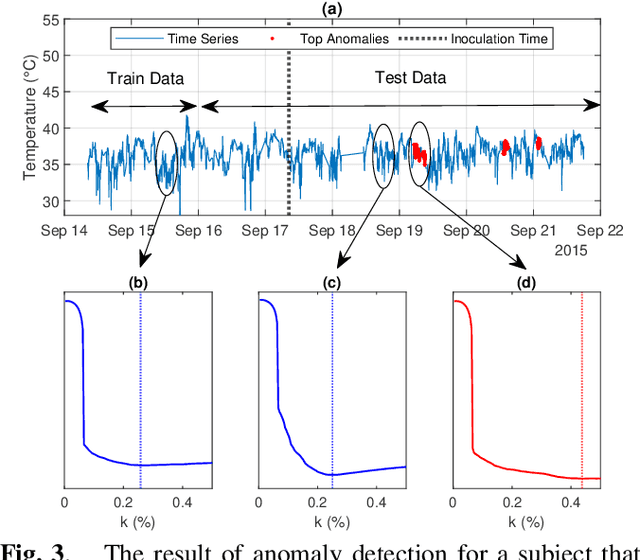
Sparse representation has been widely used in data compression, signal and image denoising, dimensionality reduction and computer vision. While overcomplete dictionaries are required for sparse representation of multidimensional data, orthogonal bases represent one-dimensional data well. In this paper, we propose a data-driven sparse representation using orthonormal bases under the lossless compression constraint. We show that imposing such constraint under the Minimum Description Length (MDL) principle leads to a unique and optimal sparse representation for one-dimensional data, which results in discriminative features useful for data discovery.