Iterative Sketching for Secure Coded Regression
Paper and Code
Aug 08, 2023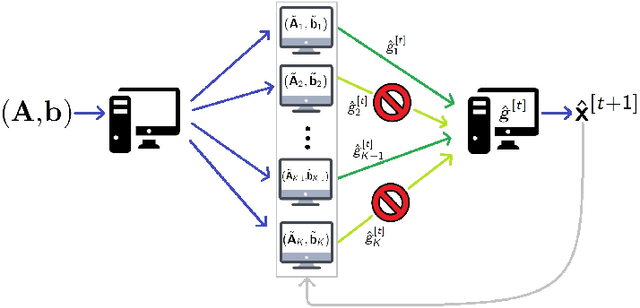
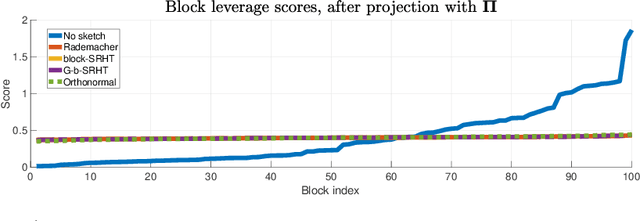
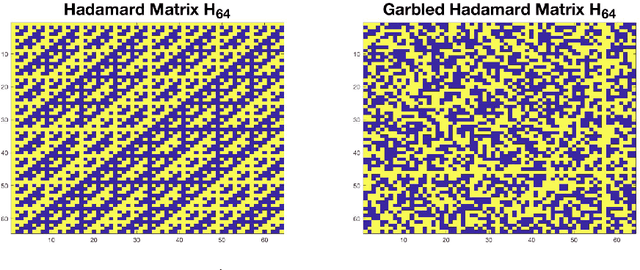
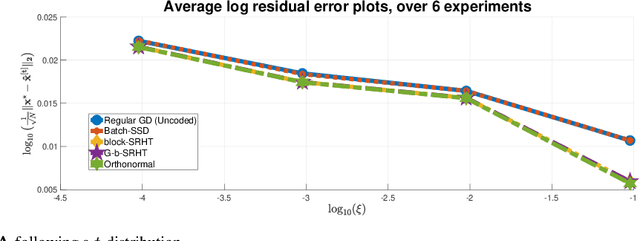
In this work, we propose methods for speeding up linear regression distributively, while ensuring security. We leverage randomized sketching techniques, and improve straggler resilience in asynchronous systems. Specifically, we apply a random orthonormal matrix and then subsample \textit{blocks}, to simultaneously secure the information and reduce the dimension of the regression problem. In our setup, the transformation corresponds to an encoded encryption in an \textit{approximate gradient coding scheme}, and the subsampling corresponds to the responses of the non-straggling workers; in a centralized coded computing network. This results in a distributive \textit{iterative sketching} approach for an $\ell_2$-subspace embedding, \textit{i.e.} a new sketch is considered at each iteration. We also focus on the special case of the \textit{Subsampled Randomized Hadamard Transform}, which we generalize to block sampling; and discuss how it can be modified in order to secure the data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge