Distributed Hybrid Sketching for $\ell_2$-Embeddings

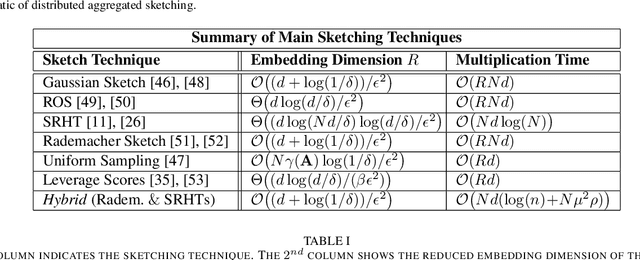
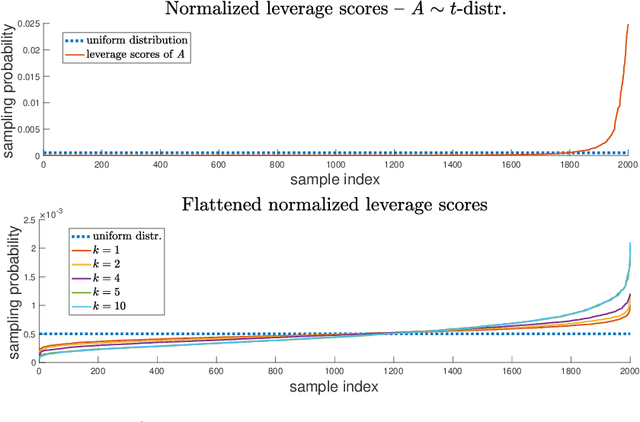
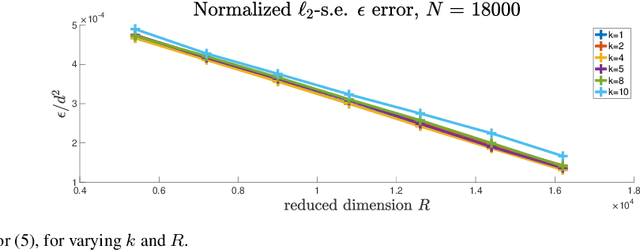
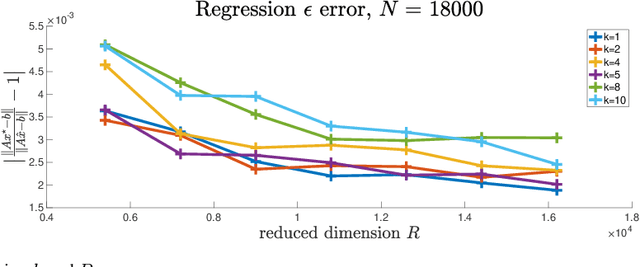
Linear algebraic operations are ubiquitous in engineering applications, and arise often in a variety of fields including statistical signal processing and machine learning. With contemporary large datasets, to perform linear algebraic methods and regression tasks, it is necessary to resort to both distributed computations as well as data compression. In this paper, we study \textit{distributed} $\ell_2$-subspace embeddings, a common technique used to efficiently perform linear regression. In our setting, data is distributed across multiple computing nodes and a goal is to minimize communication between the nodes and the coordinator in the distributed centralized network, while maintaining the geometry of the dataset. Furthermore, there is also the concern of keeping the data private and secure from potential adversaries. In this work, we address these issues through randomized sketching, where the key idea is to apply distinct sketching matrices on the local datasets. A novelty of this work is that we also consider \textit{hybrid sketching}, \textit{i.e.} a second sketch is applied on the aggregated locally sketched datasets, for enhanced embedding results. One of the main takeaways of this work is that by hybrid sketching, we can interpolate between the trade-offs that arise in off-the-shelf sketching matrices. That is, we can obtain gains in terms of embedding dimension or multiplication time. Our embedding arguments are also justified numerically.

Iterative Sketching for Secure Coded Regression

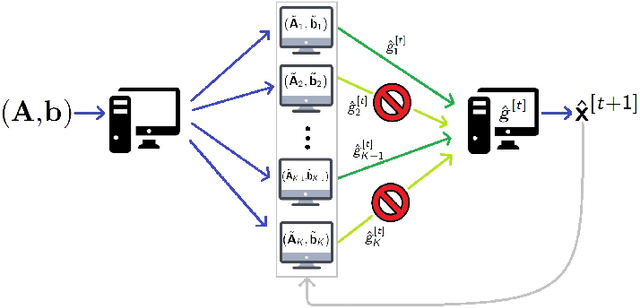
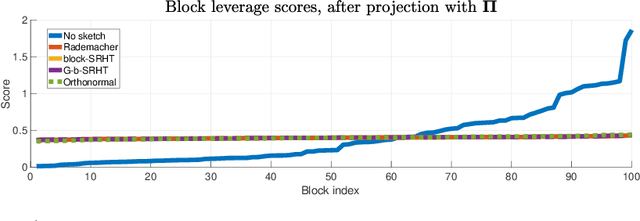
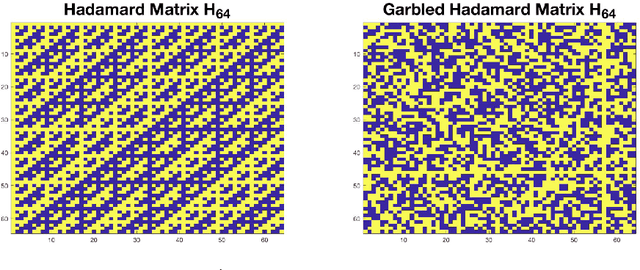
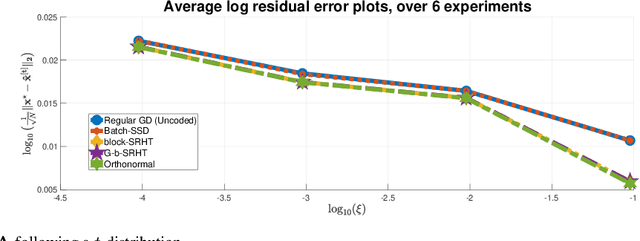
In this work, we propose methods for speeding up linear regression distributively, while ensuring security. We leverage randomized sketching techniques, and improve straggler resilience in asynchronous systems. Specifically, we apply a random orthonormal matrix and then subsample \textit{blocks}, to simultaneously secure the information and reduce the dimension of the regression problem. In our setup, the transformation corresponds to an encoded encryption in an \textit{approximate gradient coding scheme}, and the subsampling corresponds to the responses of the non-straggling workers; in a centralized coded computing network. This results in a distributive \textit{iterative sketching} approach for an $\ell_2$-subspace embedding, \textit{i.e.} a new sketch is considered at each iteration. We also focus on the special case of the \textit{Subsampled Randomized Hadamard Transform}, which we generalize to block sampling; and discuss how it can be modified in order to secure the data.

Gradient Coding through Iterative Block Leverage Score Sampling

We generalize the leverage score sampling sketch for $\ell_2$-subspace embeddings, to accommodate sampling subsets of the transformed data, so that the sketching approach is appropriate for distributed settings. This is then used to derive an approximate coded computing approach for first-order methods; known as gradient coding, to accelerate linear regression in the presence of failures in distributed computational networks, \textit{i.e.} stragglers. We replicate the data across the distributed network, to attain the approximation guarantees through the induced sampling distribution. The significance and main contribution of this work, is that it unifies randomized numerical linear algebra with approximate coded computing, while attaining an induced $\ell_2$-subspace embedding through uniform sampling. The transition to uniform sampling is done without applying a random projection, as in the case of the subsampled randomized Hadamard transform. Furthermore, by incorporating this technique to coded computing, our scheme is an iterative sketching approach to approximately solving linear regression. We also propose weighting when sketching takes place through sampling with replacement, for further compression.

Graph Sparsification by Approximate Matrix Multiplication

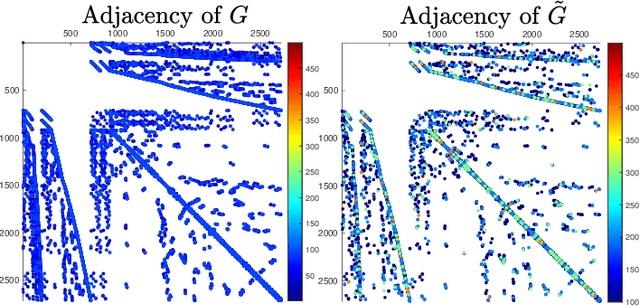
Graphs arising in statistical problems, signal processing, large networks, combinatorial optimization, and data analysis are often dense, which causes both computational and storage bottlenecks. One way of \textit{sparsifying} a \textit{weighted} graph, while sharing the same vertices as the original graph but reducing the number of edges, is through \textit{spectral sparsification}. We study this problem through the perspective of RandNLA. Specifically, we utilize randomized matrix multiplication to give a clean and simple analysis of how sampling according to edge weights gives a spectral approximation to graph Laplacians. Through the $CR$-MM algorithm, we attain a simple and computationally efficient sparsifier whose resulting Laplacian estimate is unbiased and of minimum variance. Furthermore, we define a new notion of \textit{additive spectral sparsifiers}, which has not been considered in the literature.

Orthonormal Sketches for Secure Coded Regression}

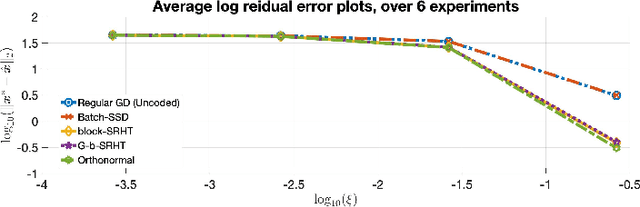
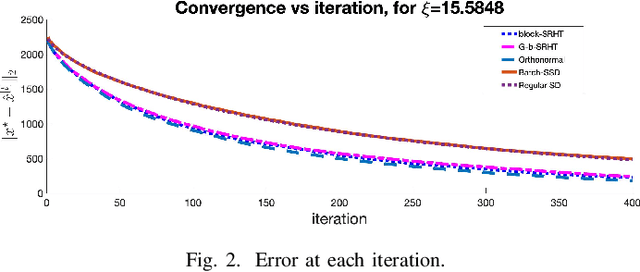
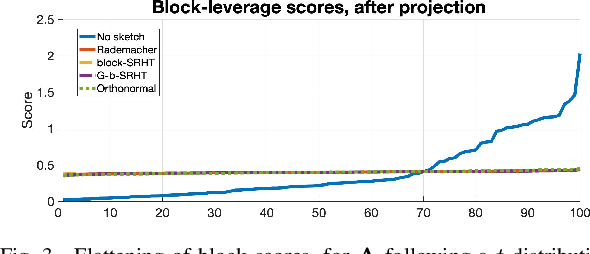
In this work, we propose a method for speeding up linear regression distributively, while ensuring security. We leverage randomized sketching techniques, and improve straggler resilience in asynchronous systems. Specifically, we apply a random orthonormal matrix and then subsample in \textit{blocks}, to simultaneously secure the information and reduce the dimension of the regression problem. In our setup, the transformation corresponds to an encoded encryption in an \textit{approximate} gradient coding scheme, and the subsampling corresponds to the responses of the non-straggling workers; in a centralized coded computing network. We focus on the special case of the \textit{Subsampled Randomized Hadamard Transform}, which we generalize to block sampling; and discuss how it can be used to secure the data. We illustrate the performance through numerical experiments.

Dimensionality Reduction for $k$-means Clustering

We present a study on how to effectively reduce the dimensions of the $k$-means clustering problem, so that provably accurate approximations are obtained. Four algorithms are presented, two \textit{feature selection} and two \textit{feature extraction} based algorithms, all of which are randomized.