Deep Reinforcement Learning-Aided Strategies for Big Data Offloading in Vehicular Networks

We consider vehicular networking scenarios where existing vehicle-to-vehicle (V2V) links can be leveraged for an effective uploading of large-size data to the network. In particular, we consider a group of vehicles where one vehicle can be designated as the \textit{leader} and other \textit{follower} vehicles can offload their data to the leader vehicle or directly upload it to the base station (or a combination of the two). In our proposed framework, the leader vehicle is responsible for receiving the data from other vehicles and processing it in order to remove the redundancy (deduplication) before uploading it to the base station. We present a mathematical framework of the considered network and formulate two separate optimization problems for minimizing (i) total time and (ii) total energy consumption by vehicles for uploading their data to the base station. We employ deep reinforcement learning (DRL) tools to obtain solutions in a dynamic vehicular network where network parameters (e.g., vehicle locations and channel coefficients) vary over time. Our results demonstrate that the application of DRL is highly beneficial, and data offloading with deduplication can significantly reduce the time and energy consumption. Furthermore, we present comprehensive numerical results to validate our findings and compare them with alternative approaches to show the benefits of the proposed DRL methods.

Deep Learning-Enabled Multi-Tag Detection in Ambient Backscatter Communications

Ambient backscatter communication (AmBC) enables battery-free connectivity by letting passive tags modulate existing RF signals, but reliable detection of multiple tags is challenging due to strong direct link interference, very weak backscatter signals, and an exponentially large joint state space. Classical multi-hypothesis likelihood ratio tests (LRTs) are optimal for this task when perfect channel state information (CSI) is available, yet in AmBC such CSI is difficult to obtain and track because the RF source is uncooperative and the tags are low-power passive devices. We first derive analytical performance bounds for an LRT receiver with perfect CSI to serve as a benchmark. We then propose two complementary deep learning frameworks that relax the CSI requirement while remaining modulation-agnostic. EmbedNet is an end-to-end prototypical network that maps covariance features of the received signal directly to multi-tag states. ChanEstNet is a hybrid scheme in which a convolutional neural network estimates effective channel coefficients from pilot symbols and passes them to a conventional LRT for interpretable multi-hypothesis detection. Simulations over diverse ambient sources and system configurations show that the proposed methods substantially reduce bit error rate, closely track the LRT benchmark, and significantly outperform energy detection baselines, especially as the number of tags increases.

Efficient Covering Using Reed--Solomon Codes

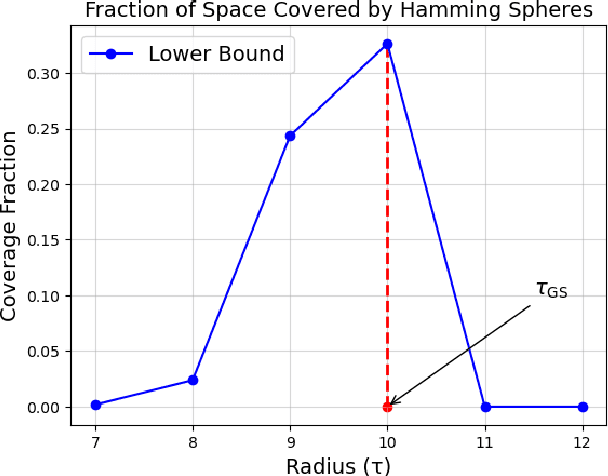
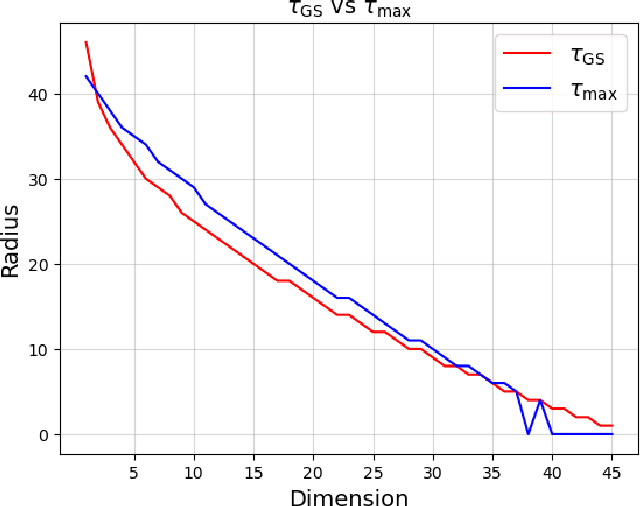
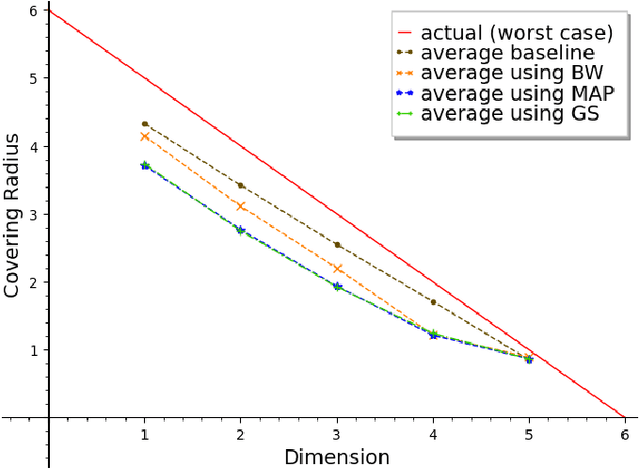
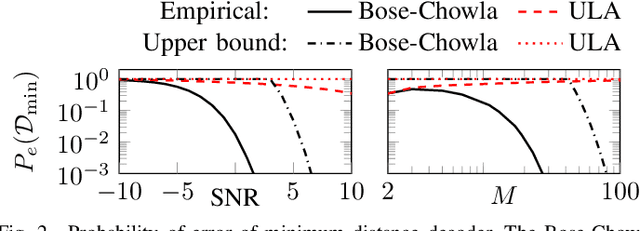
We propose an efficient algorithm to find a Reed-Solomon (RS) codeword at a distance within the covering radius of the code from any point in its ambient Hamming space. To the best of the authors' knowledge, this is the first attempt of its kind to solve the covering problem for RS codes. The proposed algorithm leverages off-the-shelf decoding methods for RS codes, including the Berlekamp-Welch algorithm for unique decoding and the Guruswami-Sudan algorithm for list decoding. We also present theoretical and numerical results on the capabilities of the proposed algorithm and, in particular, the average covering radius resulting from it. Our numerical results suggest that the overlapping Hamming spheres of radius close to the Guruswami-Sudan decoding radius centered at the codewords cover most of the ambient Hamming space.

Precoding Design for Limited-Feedback MISO Systems via Character-Polynomial Codes

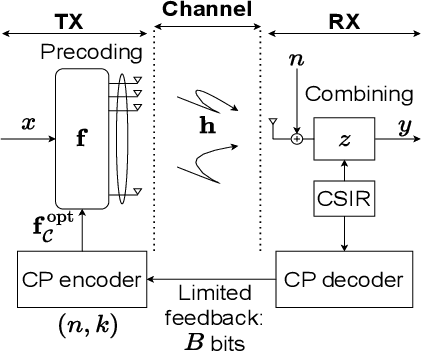
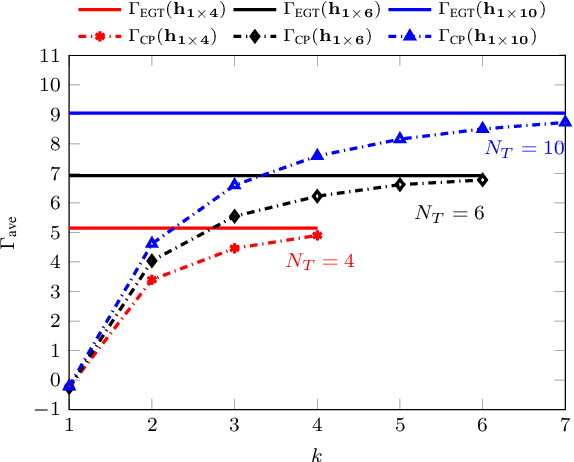
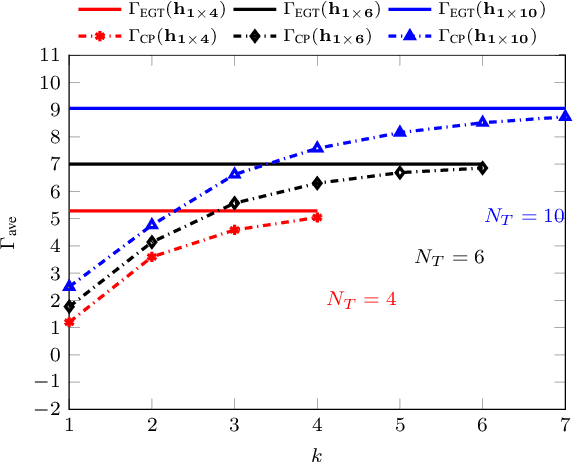
We consider the problem of Multiple-Input Single- Output (MISO) communication with limited feedback, where the transmitter relies on a limited number of bits associated with the channel state information (CSI), available at the receiver (CSIR) but not at the transmitter (no CSIT), sent via the feedback link. We demonstrate how character-polynomial (CP) codes, a class of analog subspace codes (also, referred to as Grassmann codes) can be used for the corresponding quantization problem in the Grassmann space. The proposed CP codebook-based precoding design allows for a smooth trade-off between the number of feedback bits and the beamforming gain, by simply adjusting the rate of the underlying CP code. We present a theoretical upper bound on the mean squared quantization error of the CP codebook, and utilize it to upper bound the resulting distortion as the normalized gap between the CP codebook beamforming gain and the baseline equal gain transmission (EGT) with perfect CSIT. We further show that the distortion vanishes asymptotically. The results are also confirmed via simulations for different types of fading models in the MISO system and various parameters.

Decoding Analog Subspace Codes: Algorithms for Character-Polynomial Codes

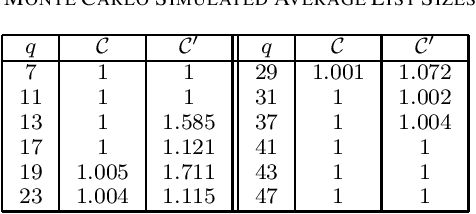
We propose efficient minimum-distance decoding and list-decoding algorithms for a certain class of analog subspace codes, referred to as character-polynomial (CP) codes, recently introduced by Soleymani and the second author. In particular, a CP code without its character can be viewed as a subcode of a Reed--Solomon (RS) code, where a certain subset of the coefficients of the message polynomial is set to zeros. We then demonstrate how classical decoding methods, including list decoders, for RS codes can be leveraged for decoding CP codes. For instance, it is shown that, in almost all cases, the list decoder behaves as a unique decoder. We also present a probabilistic analysis of the improvements in list decoding of CP codes when leveraging their certain structure as subcodes of RS codes.

Subspace Coding for Spatial Sensing

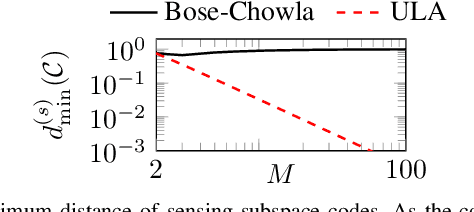
A subspace code is defined as a collection of subspaces of an ambient vector space, where each information-encoding codeword is a subspace. This paper studies a class of spatial sensing problems, notably direction of arrival (DoA) estimation using multisensor arrays, from a novel subspace coding perspective. Specifically, we demonstrate how a canonical (passive) sensing model can be mapped into a subspace coding problem, with the sensing operation defining a unique structure for the subspace codewords. We introduce the concept of sensing subspace codes following this structure, and show how these codes can be controlled by judiciously designing the sensor array geometry. We further present a construction of sensing subspace codes leveraging a certain class of Golomb rulers that achieve near-optimal minimum codeword distance. These designs inspire novel noise-robust sparse array geometries achieving high angular resolution. We also prove that codes corresponding to conventional uniform linear arrays are suboptimal in this regard. This work is the first to establish connections between subspace coding and spatial sensing, with the aim of leveraging insights and methodologies in one field to tackle challenging problems in the other.

DREW : Towards Robust Data Provenance by Leveraging Error-Controlled Watermarking

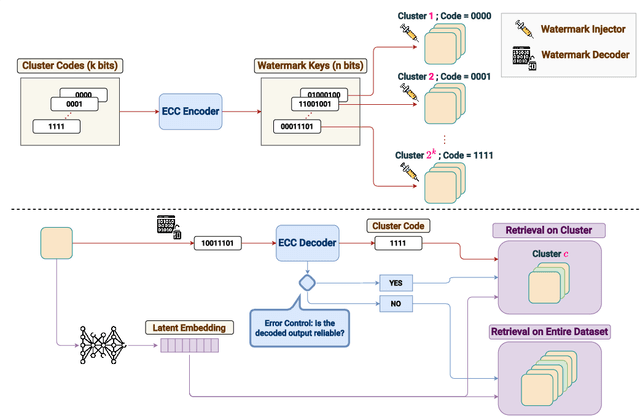
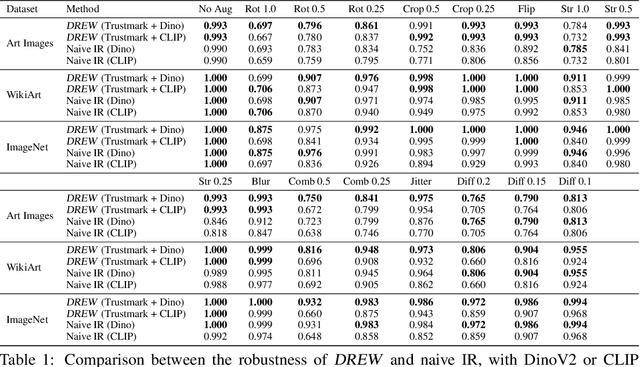
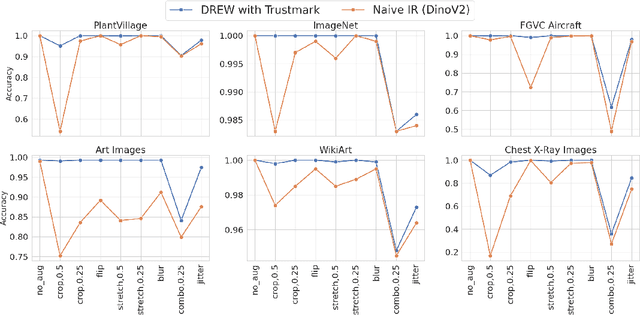
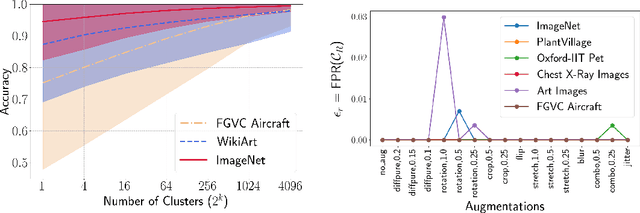
Identifying the origin of data is crucial for data provenance, with applications including data ownership protection, media forensics, and detecting AI-generated content. A standard approach involves embedding-based retrieval techniques that match query data with entries in a reference dataset. However, this method is not robust against benign and malicious edits. To address this, we propose Data Retrieval with Error-corrected codes and Watermarking (DREW). DREW randomly clusters the reference dataset, injects unique error-controlled watermark keys into each cluster, and uses these keys at query time to identify the appropriate cluster for a given sample. After locating the relevant cluster, embedding vector similarity retrieval is performed within the cluster to find the most accurate matches. The integration of error control codes (ECC) ensures reliable cluster assignments, enabling the method to perform retrieval on the entire dataset in case the ECC algorithm cannot detect the correct cluster with high confidence. This makes DREW maintain baseline performance, while also providing opportunities for performance improvements due to the increased likelihood of correctly matching queries to their origin when performing retrieval on a smaller subset of the dataset. Depending on the watermark technique used, DREW can provide substantial improvements in retrieval accuracy (up to 40\% for some datasets and modification types) across multiple datasets and state-of-the-art embedding models (e.g., DinoV2, CLIP), making our method a promising solution for secure and reliable source identification. The code is available at https://github.com/mehrdadsaberi/DREW

Iterative Sketching for Secure Coded Regression

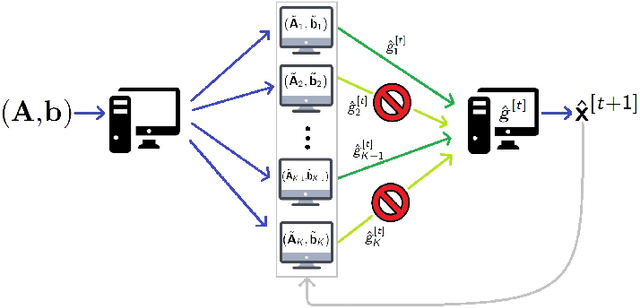
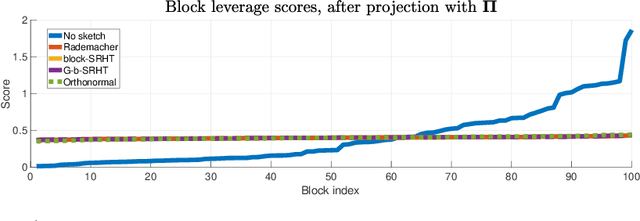
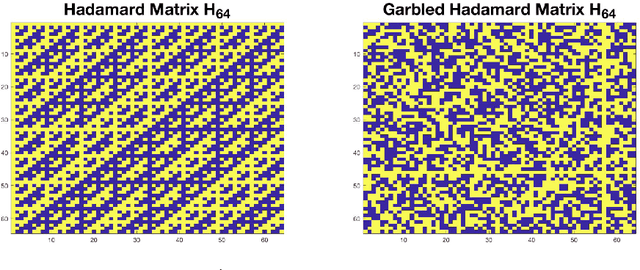
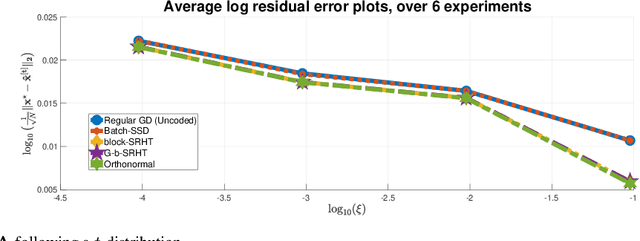
In this work, we propose methods for speeding up linear regression distributively, while ensuring security. We leverage randomized sketching techniques, and improve straggler resilience in asynchronous systems. Specifically, we apply a random orthonormal matrix and then subsample \textit{blocks}, to simultaneously secure the information and reduce the dimension of the regression problem. In our setup, the transformation corresponds to an encoded encryption in an \textit{approximate gradient coding scheme}, and the subsampling corresponds to the responses of the non-straggling workers; in a centralized coded computing network. This results in a distributive \textit{iterative sketching} approach for an $\ell_2$-subspace embedding, \textit{i.e.} a new sketch is considered at each iteration. We also focus on the special case of the \textit{Subsampled Randomized Hadamard Transform}, which we generalize to block sampling; and discuss how it can be modified in order to secure the data.

Capacity-achieving Polar-based Codes with Sparsity Constraints on the Generator Matrices

In this paper, we leverage polar codes and the well-established channel polarization to design capacity-achieving codes with a certain constraint on the weights of all the columns in the generator matrix (GM) while having a low-complexity decoding algorithm. We first show that given a binary-input memoryless symmetric (BMS) channel $W$ and a constant $s \in (0, 1]$, there exists a polarization kernel such that the corresponding polar code is capacity-achieving with the \textit{rate of polarization} $s/2$, and the GM column weights being bounded from above by $N^s$. To improve the sparsity versus error rate trade-off, we devise a column-splitting algorithm and two coding schemes for BEC and then for general BMS channels. The \textit{polar-based} codes generated by the two schemes inherit several fundamental properties of polar codes with the original $2 \times 2$ kernel including the decay in error probability, decoding complexity, and the capacity-achieving property. Furthermore, they demonstrate the additional property that their GM column weights are bounded from above sublinearly in $N$, while the original polar codes have some column weights that are linear in $N$. In particular, for any BEC and $\beta <0.5$, the existence of a sequence of capacity-achieving polar-based codes where all the GM column weights are bounded from above by $N^\lambda$ with $\lambda \approx 0.585$, and with the error probability bounded by $O(2^{-N^{\beta}} )$ under a decoder with complexity $O(N\log N)$, is shown. The existence of similar capacity-achieving polar-based codes with the same decoding complexity is shown for any BMS channel and $\beta <0.5$ with $\lambda \approx 0.631$.

Machine Learning-Aided Efficient Decoding of Reed-Muller Subcodes

Reed-Muller (RM) codes achieve the capacity of general binary-input memoryless symmetric channels and have a comparable performance to that of random codes in terms of scaling laws. However, they lack efficient decoders with performance close to that of a maximum-likelihood decoder for general code parameters. Also, they only admit limited sets of rates. In this paper, we focus on subcodes of RM codes with flexible rates. We first extend the recently-introduced recursive projection-aggregation (RPA) decoding algorithm to RM subcodes. To lower the complexity of our decoding algorithm, referred to as subRPA, we investigate different approaches to prune the projections. Next, we derive the soft-decision based version of our algorithm, called soft-subRPA, that not only improves upon the performance of subRPA but also enables a differentiable decoding algorithm. Building upon the soft-subRPA algorithm, we then provide a framework for training a machine learning (ML) model to search for \textit{good} sets of projections that minimize the decoding error rate. Training our ML model enables achieving very close to the performance of full-projection decoding with a significantly smaller number of projections. We also show that the choice of the projections in decoding RM subcodes matters significantly, and our ML-aided projection pruning scheme is able to find a \textit{good} selection, i.e., with negligible performance degradation compared to the full-projection case, given a reasonable number of projections.