Beyond-Diagonal RIS: Adversarial Channels and Optimality of Low-Complexity Architectures

Beyond-diagonal reconfigurable intelligent surfaces (BD-RISs) have recently gained attention as an enhancement to conventional RISs. BD-RISs allow optimizing not only the phase, but also the amplitude responses of their discrete surface elements by introducing adjustable inter-element couplings. Various BD-RIS architectures have been proposed to optimally trade off between average performance and complexity of the architecture. However, little attention has been paid to worst-case performance. This paper characterizes novel sets of adversarial channels for which certain low-complexity BD-RIS architectures have suboptimal performance in terms of received signal power at an intended communications user. Specifically, we consider two recent BD-RIS models: the so-called group-connected and tree-connected architecture. The derived adversarial channel sets reveal new surprising connections between the two architectures. We validate our analytical results numerically, demonstrating that adversarial channels can cause a significant performance loss. Our results pave the way towards efficient BD-RIS designs that are robust to adversarial propagation conditions and malicious attacks.

Jointly optimal array geometries and waveforms in active sensing: New insights into array design via the Cramér-Rao bound

This paper investigates jointly optimal array geometry and waveform designs for active sensing. Specifically, we focus on minimizing the Cram\'er-Rao lower bound (CRB) of the angle of a single target in white Gaussian noise. We first find that several array-waveform pairs can yield the same CRB by virtue of sequences with equal sums of squares, i.e., solutions to certain Diophantine equations. Furthermore, we show that under physical aperture and sensor number constraints, the CRB-minimizing receive array geometry is unique, whereas the transmit array can be chosen flexibly. We leverage this freedom to design a novel sparse array geometry that not only minimizes the single-target CRB given an optimal waveform, but also has a nonredundant and contiguous sum co-array, a desirable property when launching independent waveforms, with relevance also to the multi-target case.

Generative Deep Synthesis of MIMO Sensing Waveforms with Desired Transmit Beampattern

This paper develops a generative deep learning model for the synthesis of multiple-input multiple-output (MIMO) active sensing waveforms with desired properties, including constant modulus and a user-defined beampattern. The proposed approach is capable synthesizing unique phase codes of on-the-fly, which has the potential to reduce interference between co-existing active sensing systems and facilitate Low Probability of Intercept/Low Probability of Detection (LPI/LPD) radar operation. The paper extends our earlier work on synthesis of approximately orthogonal MIMO phase codes by introducing flexible control over the transmit beampatterns. The developed machine learning method employs a conditional Wasserstein Generative Adversarial Network (GAN) structure. The main benefits of the method are its ability to discover new waveforms on-demand (post training) and generate demanding beampatterns at lower computational complexity compared to structured optimization approaches.

Sparse Array Sensor Selection in ISAC with Identifiability Guarantees

This paper investigates array geometry and waveform design for integrated sensing and communications (ISAC) employing sensor selection. We consider ISAC via index modulation, where various subsets of transmit (Tx) sensors are used for both communications and monostatic active sensing. The set of Tx subarrays make up a codebook, whose cardinality we maximize (for communications) subject to guaranteeing a desired target identifiability (for sensing). To characterize the size of this novel optimal codebook, we derive first upper and lower bounds, which are tight in case of the canonical uniform linear array (ULA) and any nonredundant array. We show that the ULA achieves a large codebook - comparable to the size of the conventional unconstrained case - as satisfying the identifiability constraint only requires including two specific sensors in each Tx subarray (codeword). In contrast, nonredundant arrays, which have the largest identifiability for a given number of physical sensors, only have a single admissible codeword, rendering them ineffectual for communications via sensor selection alone. The results serve as a step towards an analytical understanding of the limits of sensor selection in ISAC and the fundamental trade-offs therein.

Subspace Coding for Spatial Sensing

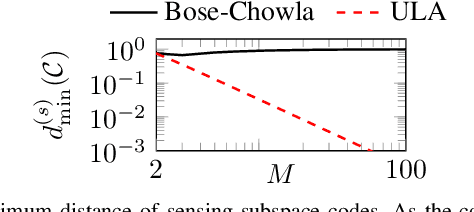
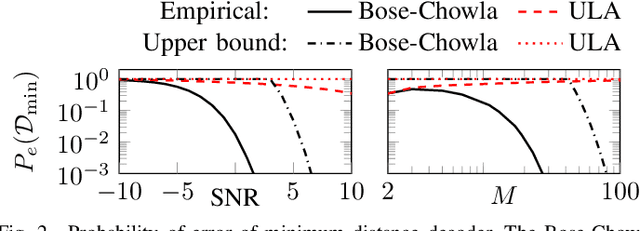
A subspace code is defined as a collection of subspaces of an ambient vector space, where each information-encoding codeword is a subspace. This paper studies a class of spatial sensing problems, notably direction of arrival (DoA) estimation using multisensor arrays, from a novel subspace coding perspective. Specifically, we demonstrate how a canonical (passive) sensing model can be mapped into a subspace coding problem, with the sensing operation defining a unique structure for the subspace codewords. We introduce the concept of sensing subspace codes following this structure, and show how these codes can be controlled by judiciously designing the sensor array geometry. We further present a construction of sensing subspace codes leveraging a certain class of Golomb rulers that achieve near-optimal minimum codeword distance. These designs inspire novel noise-robust sparse array geometries achieving high angular resolution. We also prove that codes corresponding to conventional uniform linear arrays are suboptimal in this regard. This work is the first to establish connections between subspace coding and spatial sensing, with the aim of leveraging insights and methodologies in one field to tackle challenging problems in the other.

Sparse Spatial Smoothing: Reduced Complexity and Improved Beamforming Gain via Sparse Sub-Arrays

This paper addresses the problem of single snapshot Direction-of-Arrival (DOA) estimation, which is of great importance in a wide-range of applications including automotive radar. A popular approach to achieving high angular resolution when only one temporal snapshot is available is via subspace methods using spatial smoothing. This involves leveraging spatial shift-invariance in the antenna array geometry, typically a uniform linear array (ULA), to rearrange the single snapshot measurement vector into a spatially smoothed matrix that reveals the signal subspace of interest. However, conventional approaches using spatially shifted ULA sub-arrays can lead to a prohibitively high computational complexity due to the large dimensions of the resulting spatially smoothed matrix. Hence, we propose to instead employ judiciously designed sparse sub-arrays, such as nested arrays, to reduce the computational complexity of spatial smoothing while retaining the aperture and identifiability of conventional ULA-based approaches. Interestingly, this idea also suggests a novel beamforming method which linearly combines multiple spatially smoothed matrices corresponding to different sets of shifts of the sparse (nested) sub-array. This so-called shift-domain beamforming method is demonstrated to boost the effective SNR, and thereby resolution, in a desired angular region of interest, enabling single snapshot low-complexity DOA estimation with identifiability guarantees.

Importance of array redundancy pattern in active sensing

This paper further investigates the role of the array geometry and redundancy in active sensing. We are interested in the fundamental question of how many point scatterers can be identified (in the angular domain) by a given array geometry using a certain number of linearly independent transmit waveforms. We consider redundant array configurations (with repeated virtual transmit-receive sensors), which we have recently shown to be able to achieve their maximal identifiability while transmitting fewer independent waveforms than transmitters. Reducing waveform rank in this manner can be beneficial in various ways. For example, it may free up spatial resources for transmit beamforming. In this paper, we show that two array geometries with identical sum co-arrays, and the same number of physical and virtual sensors, need not achieve equal identifiability, regardless of the choice of waveform of a fixed reduced rank. This surprising result establishes the important role the pattern (not just the number) of repeated virtual sensors has in governing identifiability, and reveals the limits of compensating for unfavorable array geometries via waveform design.

Effect of Beampattern on Matrix Completion with Sparse Arrays

We study the problem of noisy sparse array interpolation, where a large virtual array is synthetically generated by interpolating missing sensors using matrix completion techniques that promote low rank. The current understanding is quite limited regarding the effect of the (sparse) array geometry on the angle estimation error (post interpolation) of these methods. In this paper, we make advances towards solidifying this understanding by revealing the role of the physical beampattern of the sparse array on the performance of low rank matrix completion techniques. When the beampattern is analytically tractable (such as for uniform linear arrays and nested arrays), our analysis provides concrete and interpretable bounds on the scaling of the angular error as a function of the number of sensors, and demonstrates the effectiveness of nested arrays in presence of noise and a single temporal snapshot.

Harnessing Holes for Spatial Smoothing with Applications in Automotive Radar

This paper studies spatial smoothing using sparse arrays in single-snapshot Direction of Arrival (DOA) estimation. We consider the application of automotive MIMO radar, which traditionally synthesizes a large uniform virtual array by appropriate waveform and physical array design. We explore deliberately introducing holes into this virtual array to leverage resolution gains provided by the increased aperture. The presence of these holes requires re-thinking DOA estimation, as conventional algorithms may no longer be easily applicable and alternative techniques, such as array interpolation, may be computationally expensive. Consequently, we study sparse array geometries that permit the direct application of spatial smoothing. We show that a sparse array geometry is amenable to spatial smoothing if it can be decomposed into the sum set of two subsets of suitable cardinality. Furthermore, we demonstrate that many such decompositions may exist - not all of them yielding equal identifiability or aperture. We derive necessary and sufficient conditions to guarantee identifiability of a given number of targets, which gives insight into choosing desirable decompositions for spatial smoothing. This provides uniform recovery guarantees and enables estimating DOAs at increased resolution and reduced computational complexity.

On array geometry and self-interference in full-duplex massive MIMO communications

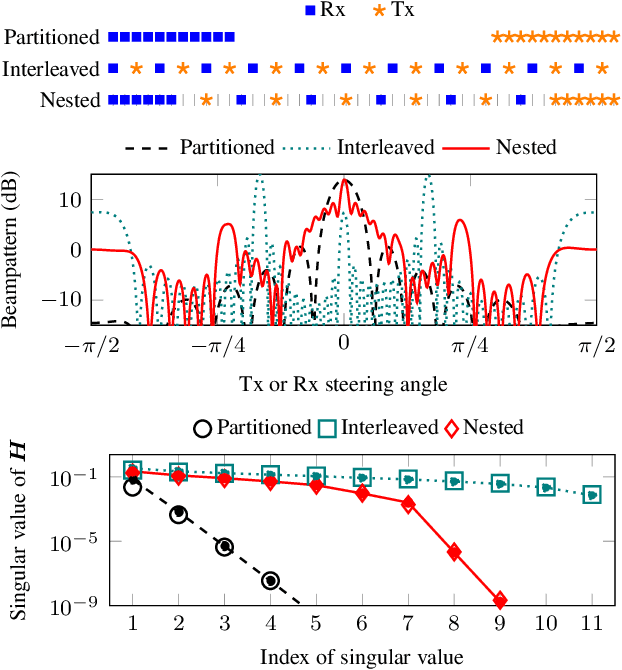
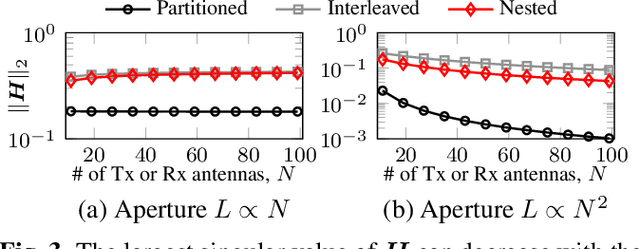
This paper studies the role of the joint transmit-receive antenna array geometry in shaping the self-interference (SI) channel in full-duplex communications. We consider a simple spherical wave SI model and two prototypical linear array geometries with uniformly spaced transmit and receive antennas. We show that the resulting SI channel matrix has a regular (Toeplitz) structure in both of these cases. However, the number of significant singular values of these matrices - an indication of the severity of SI - can be markedly different. We demonstrate that both reduced SI and high angular resolution can be obtained by employing suitable sparse array configurations that fully leverage the available joint transmit-receive array aperture without suffering from angular ambiguities. Numerical electromagnetic simulations also suggest that the worst-case SI of such sparse arrays need not increase - but can actually decrease - with the number of antennas. Our findings provide preliminary insight into the extent to which the array geometry alone can mitigate SI in full-duplex massive MIMO communications systems employing a large number of antennas.