Subspace Coding for Spatial Sensing

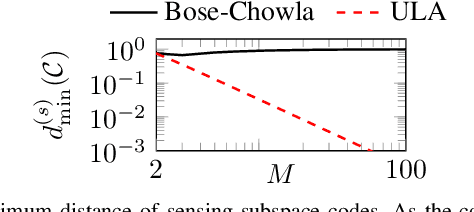
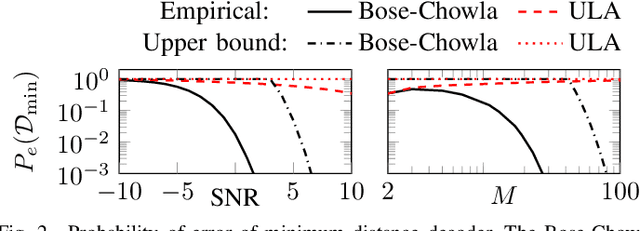
A subspace code is defined as a collection of subspaces of an ambient vector space, where each information-encoding codeword is a subspace. This paper studies a class of spatial sensing problems, notably direction of arrival (DoA) estimation using multisensor arrays, from a novel subspace coding perspective. Specifically, we demonstrate how a canonical (passive) sensing model can be mapped into a subspace coding problem, with the sensing operation defining a unique structure for the subspace codewords. We introduce the concept of sensing subspace codes following this structure, and show how these codes can be controlled by judiciously designing the sensor array geometry. We further present a construction of sensing subspace codes leveraging a certain class of Golomb rulers that achieve near-optimal minimum codeword distance. These designs inspire novel noise-robust sparse array geometries achieving high angular resolution. We also prove that codes corresponding to conventional uniform linear arrays are suboptimal in this regard. This work is the first to establish connections between subspace coding and spatial sensing, with the aim of leveraging insights and methodologies in one field to tackle challenging problems in the other.

Sparse Spatial Smoothing: Reduced Complexity and Improved Beamforming Gain via Sparse Sub-Arrays

This paper addresses the problem of single snapshot Direction-of-Arrival (DOA) estimation, which is of great importance in a wide-range of applications including automotive radar. A popular approach to achieving high angular resolution when only one temporal snapshot is available is via subspace methods using spatial smoothing. This involves leveraging spatial shift-invariance in the antenna array geometry, typically a uniform linear array (ULA), to rearrange the single snapshot measurement vector into a spatially smoothed matrix that reveals the signal subspace of interest. However, conventional approaches using spatially shifted ULA sub-arrays can lead to a prohibitively high computational complexity due to the large dimensions of the resulting spatially smoothed matrix. Hence, we propose to instead employ judiciously designed sparse sub-arrays, such as nested arrays, to reduce the computational complexity of spatial smoothing while retaining the aperture and identifiability of conventional ULA-based approaches. Interestingly, this idea also suggests a novel beamforming method which linearly combines multiple spatially smoothed matrices corresponding to different sets of shifts of the sparse (nested) sub-array. This so-called shift-domain beamforming method is demonstrated to boost the effective SNR, and thereby resolution, in a desired angular region of interest, enabling single snapshot low-complexity DOA estimation with identifiability guarantees.

Importance of array redundancy pattern in active sensing

This paper further investigates the role of the array geometry and redundancy in active sensing. We are interested in the fundamental question of how many point scatterers can be identified (in the angular domain) by a given array geometry using a certain number of linearly independent transmit waveforms. We consider redundant array configurations (with repeated virtual transmit-receive sensors), which we have recently shown to be able to achieve their maximal identifiability while transmitting fewer independent waveforms than transmitters. Reducing waveform rank in this manner can be beneficial in various ways. For example, it may free up spatial resources for transmit beamforming. In this paper, we show that two array geometries with identical sum co-arrays, and the same number of physical and virtual sensors, need not achieve equal identifiability, regardless of the choice of waveform of a fixed reduced rank. This surprising result establishes the important role the pattern (not just the number) of repeated virtual sensors has in governing identifiability, and reveals the limits of compensating for unfavorable array geometries via waveform design.

Harnessing Holes for Spatial Smoothing with Applications in Automotive Radar

This paper studies spatial smoothing using sparse arrays in single-snapshot Direction of Arrival (DOA) estimation. We consider the application of automotive MIMO radar, which traditionally synthesizes a large uniform virtual array by appropriate waveform and physical array design. We explore deliberately introducing holes into this virtual array to leverage resolution gains provided by the increased aperture. The presence of these holes requires re-thinking DOA estimation, as conventional algorithms may no longer be easily applicable and alternative techniques, such as array interpolation, may be computationally expensive. Consequently, we study sparse array geometries that permit the direct application of spatial smoothing. We show that a sparse array geometry is amenable to spatial smoothing if it can be decomposed into the sum set of two subsets of suitable cardinality. Furthermore, we demonstrate that many such decompositions may exist - not all of them yielding equal identifiability or aperture. We derive necessary and sufficient conditions to guarantee identifiability of a given number of targets, which gives insight into choosing desirable decompositions for spatial smoothing. This provides uniform recovery guarantees and enables estimating DOAs at increased resolution and reduced computational complexity.

Effect of Beampattern on Matrix Completion with Sparse Arrays

We study the problem of noisy sparse array interpolation, where a large virtual array is synthetically generated by interpolating missing sensors using matrix completion techniques that promote low rank. The current understanding is quite limited regarding the effect of the (sparse) array geometry on the angle estimation error (post interpolation) of these methods. In this paper, we make advances towards solidifying this understanding by revealing the role of the physical beampattern of the sparse array on the performance of low rank matrix completion techniques. When the beampattern is analytically tractable (such as for uniform linear arrays and nested arrays), our analysis provides concrete and interpretable bounds on the scaling of the angular error as a function of the number of sensors, and demonstrates the effectiveness of nested arrays in presence of noise and a single temporal snapshot.

Array-Informed Waveform Design for Active Sensing: Diversity, Redundancy, and Identifiability

This paper investigates the combined role of transmit waveforms and (sparse) sensor array geometries in active sensing multiple-input multiple-output (MIMO) systems. Specifically, we consider the fundamental identifiability problem of uniquely recovering the unknown scatterer angles and coefficients from noiseless spatio-temporal measurements. Assuming a sparse scene, identifiability is determined by the Kruskal rank of a highly structured sensing matrix, which depends on both the transmitted waveforms and the array configuration. We derive necessary and sufficient conditions that the array geometry and transmit waveforms need to satisfy for the Kruskal rank -- and hence identifiability -- to be maximized. Moreover, we propose waveform designs that maximize identifiability for common array configurations. We also provide novel insights on the interaction between the waveforms and array geometry. A key observation is that waveforms should be matched to the pattern of redundant transmit-receive sensor pairs. Redundant array configurations are commonly employed to increase noise resilience, robustify against sensor failures, and improve beamforming capabilities. Our analysis also clearly shows that a redundant array is capable of achieving its maximum identifiability using fewer linearly independent waveforms than transmitters. This has the benefit of lowering hardware costs and transmission time. We illustrate our findings using multiple examples with unit-modulus waveforms, which are often preferred in practice.

Super-resolution with Sparse Arrays: A Non-Asymptotic Analysis of Spatio-temporal Trade-offs

Sparse arrays have emerged as a popular alternative to the conventional uniform linear array (ULA) due to the enhanced degrees of freedom (DOF) and superior resolution offered by them. In the passive setting, these advantages are realized by leveraging correlation between the received signals at different sensors. This has led to the belief that sparse arrays require a large number of temporal measurements to reliably estimate parameters of interest from these correlations, and therefore they may not be preferred in the sample-starved regime. In this paper, we debunk this myth by performing a rigorous non-asymptotic analysis of the Coarray ESPRIT algorithm. This seemingly counter-intuitive result is a consequence of the scaling of the singular value of the coarray manifold, which compensates for the potentially large covariance estimation error in the limited snapshot regime. Specifically, we show that for a nested array operating in the regime of fewer sources than sensors ($S=O(1)$), it is possible to bound the matching distance error between the estimated and true directions of arrival (DOAs) by an arbitrarily small quantity ($\epsilon$) with high probability, provided (i) the number of temporal snapshots ($L$) scales only logarithmically with the number of sensors ($P$), i.e. $L=\Omega(\ln(P)/\epsilon^2)$, and (ii) a suitable separation condition is satisfied. Our results also formally prove the well-known empirical resolution benefits of sparse arrays, by establishing that the minimum separation between sources can be $\Omega(1/P^2)$, as opposed to separation $\Omega(1/P)$ required by a ULA with the same number of sensors. Our sample complexity expression reveals the dependence on other key model parameters such as SNR and the dynamic range of the source powers. This enables us to establish the superior noise-resilience of nested arrays both theoretically and empirically.

Super-resolution with Binary Priors: Theory and Algorithms

The problem of super-resolution is concerned with the reconstruction of temporally/spatially localized events (or spikes) from samples of their convolution with a low-pass filter. Distinct from prior works which exploit sparsity in appropriate domains in order to solve the resulting ill-posed problem, this paper explores the role of binary priors in super-resolution, where the spike (or source) amplitudes are assumed to be binary-valued. Our study is inspired by the problem of neural spike deconvolution, but also applies to other applications such as symbol detection in hybrid millimeter wave communication systems. This paper makes several theoretical and algorithmic contributions to enable binary super-resolution with very few measurements. Our results show that binary constraints offer much stronger identifiability guarantees than sparsity, allowing us to operate in "extreme compression" regimes, where the number of measurements can be significantly smaller than the sparsity level of the spikes. To ensure exact recovery in this "extreme compression" regime, it becomes necessary to design algorithms that exactly enforce binary constraints without relaxation. In order to overcome the ensuing computational challenges, we consider a first order auto-regressive filter (which appears in neural spike deconvolution), and exploit its special structure. This results in a novel formulation of the super-resolution binary spike recovery in terms of binary search in one dimension. We perform numerical experiments that validate our theory and also show the benefits of binary constraints in neural spike deconvolution from real calcium imaging datasets.

Sampling Requirements for Stable Autoregressive Estimation

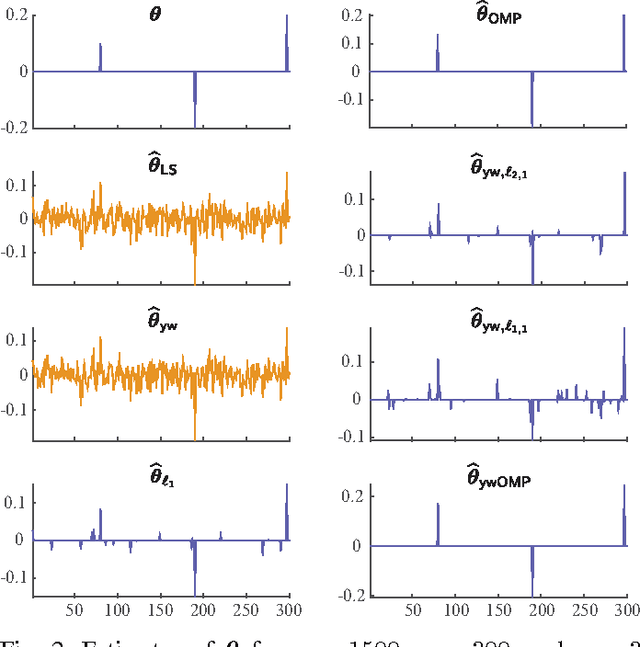
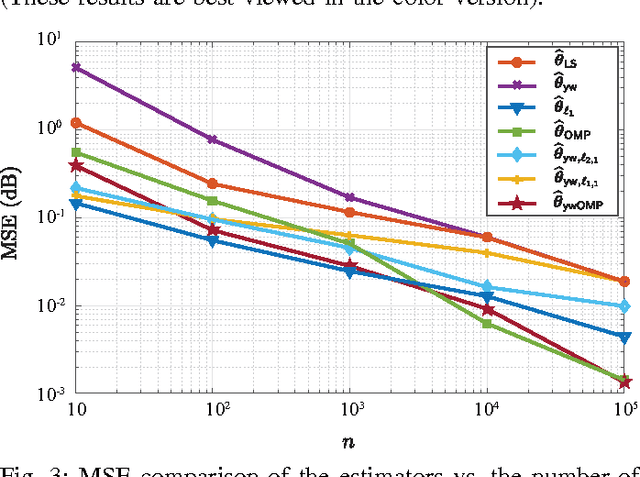
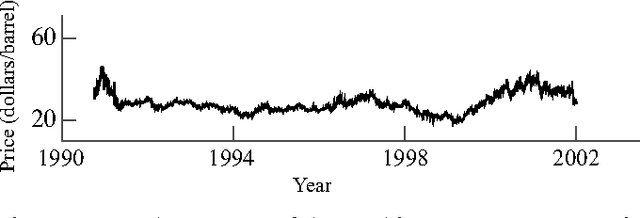
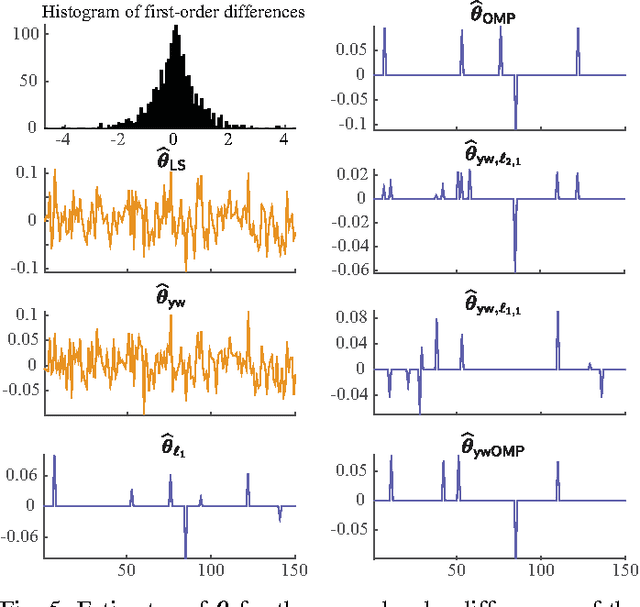
We consider the problem of estimating the parameters of a linear univariate autoregressive model with sub-Gaussian innovations from a limited sequence of consecutive observations. Assuming that the parameters are compressible, we analyze the performance of the $\ell_1$-regularized least squares as well as a greedy estimator of the parameters and characterize the sampling trade-offs required for stable recovery in the non-asymptotic regime. In particular, we show that for a fixed sparsity level, stable recovery of AR parameters is possible when the number of samples scale sub-linearly with the AR order. Our results improve over existing sampling complexity requirements in AR estimation using the LASSO, when the sparsity level scales faster than the square root of the model order. We further derive sufficient conditions on the sparsity level that guarantee the minimax optimality of the $\ell_1$-regularized least squares estimate. Applying these techniques to simulated data as well as real-world datasets from crude oil prices and traffic speed data confirm our predicted theoretical performance gains in terms of estimation accuracy and model selection.