Sampling Requirements for Stable Autoregressive Estimation
Paper and Code
Jan 17, 2017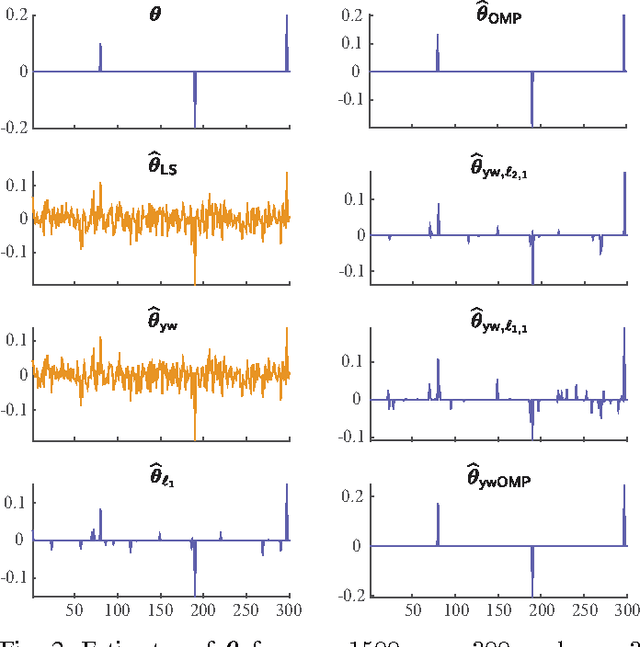
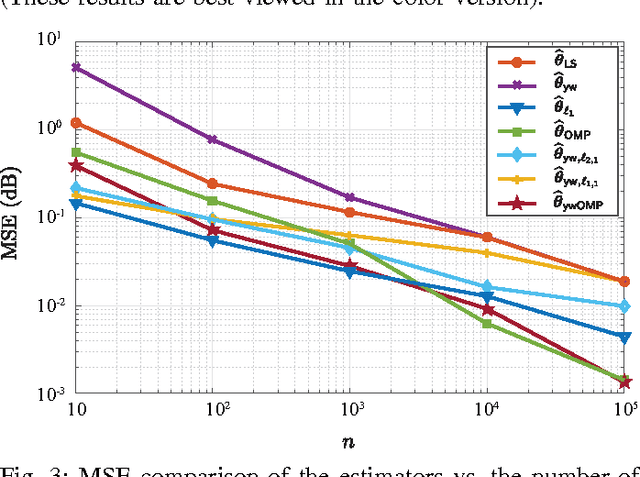
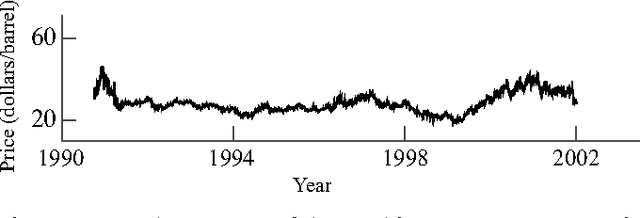
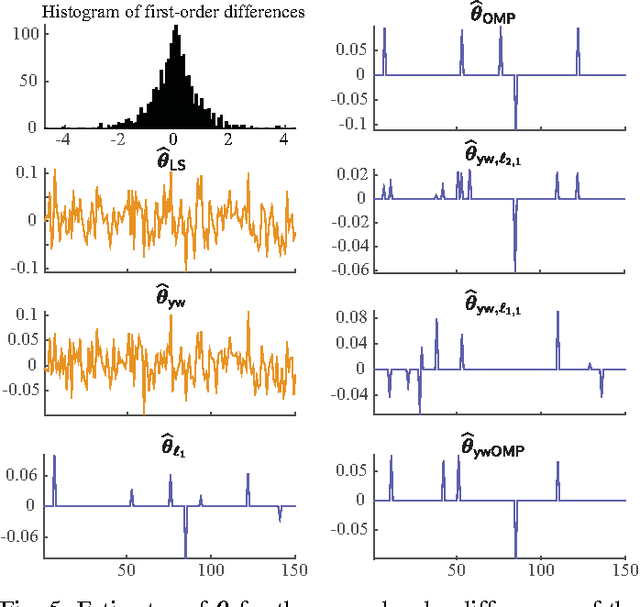
We consider the problem of estimating the parameters of a linear univariate autoregressive model with sub-Gaussian innovations from a limited sequence of consecutive observations. Assuming that the parameters are compressible, we analyze the performance of the $\ell_1$-regularized least squares as well as a greedy estimator of the parameters and characterize the sampling trade-offs required for stable recovery in the non-asymptotic regime. In particular, we show that for a fixed sparsity level, stable recovery of AR parameters is possible when the number of samples scale sub-linearly with the AR order. Our results improve over existing sampling complexity requirements in AR estimation using the LASSO, when the sparsity level scales faster than the square root of the model order. We further derive sufficient conditions on the sparsity level that guarantee the minimax optimality of the $\ell_1$-regularized least squares estimate. Applying these techniques to simulated data as well as real-world datasets from crude oil prices and traffic speed data confirm our predicted theoretical performance gains in terms of estimation accuracy and model selection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge