No Spurious Local Minima in Deep Quadratic Networks

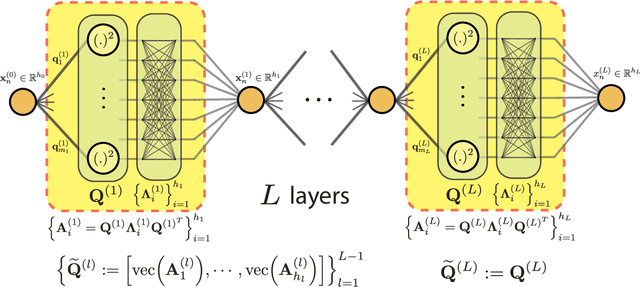
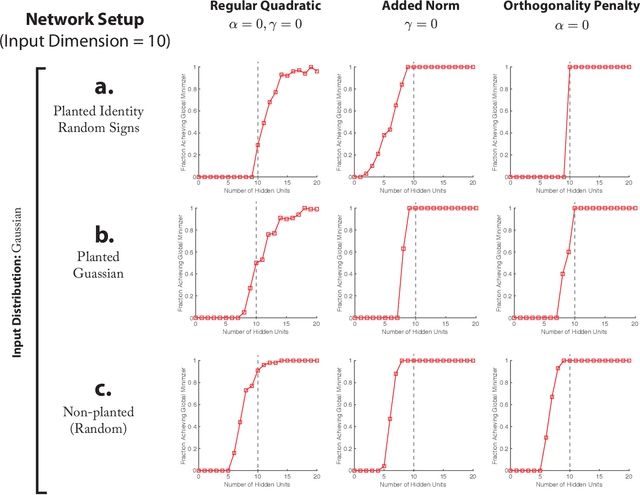
Despite their practical success, a theoretical understanding of the loss landscape of neural networks has proven challenging due to the high-dimensional, non-convex, and highly nonlinear structure of such models. In this paper, we characterize the training landscape of the quadratic loss landscape for neural networks with quadratic activation functions. We prove existence of spurious local minima and saddle points which can be escaped easily with probability one when the number of neurons is greater than or equal to the input dimension and the norm of the training samples is used as a regressor. We prove that deep overparameterized neural networks with quadratic activations benefit from similar nice landscape properties. Our theoretical results are independent of data distribution and fill the existing gap in theory for two-layer quadratic neural networks. Finally, we empirically demonstrate convergence to a global minimum for these problems.

Robust Estimation of Self-Exciting Generalized Linear Models with Application to Neuronal Modeling

We consider the problem of estimating self-exciting generalized linear models from limited binary observations, where the history of the process serves as the covariate. We analyze the performance of two classes of estimators, namely the $\ell_1$-regularized maximum likelihood and greedy estimators, for a canonical self-exciting process and characterize the sampling tradeoffs required for stable recovery in the non-asymptotic regime. Our results extend those of compressed sensing for linear and generalized linear models with i.i.d. covariates to those with highly inter-dependent covariates. We further provide simulation studies as well as application to real spiking data from the mouse's lateral geniculate nucleus and the ferret's retinal ganglion cells which agree with our theoretical predictions.

Sampling Requirements for Stable Autoregressive Estimation

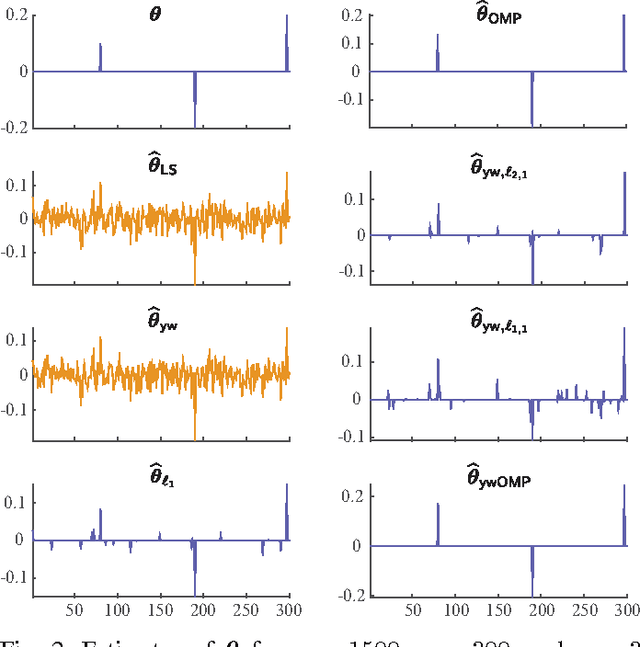
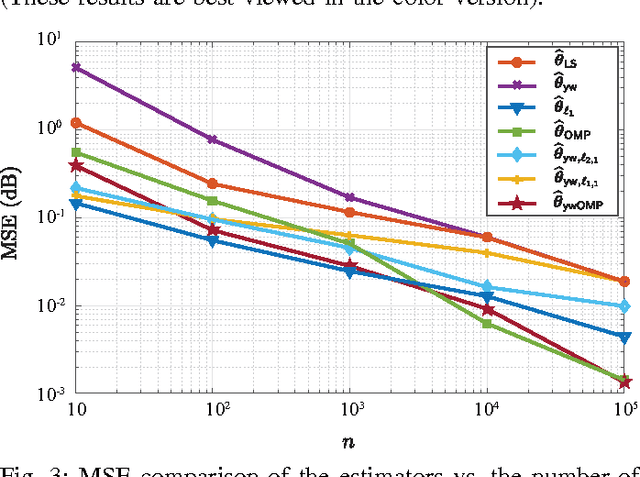
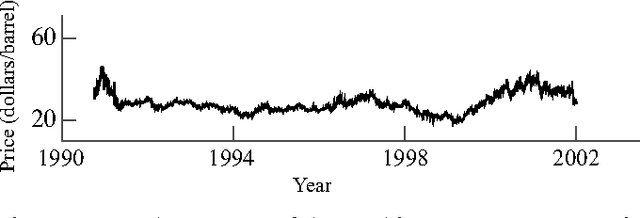
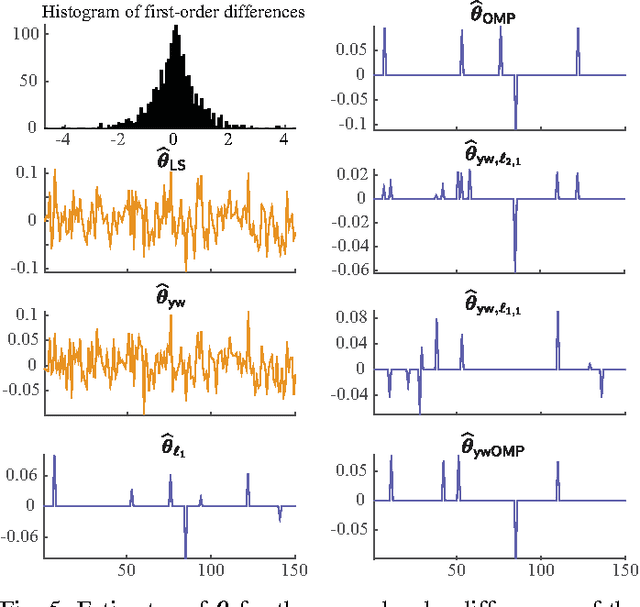
We consider the problem of estimating the parameters of a linear univariate autoregressive model with sub-Gaussian innovations from a limited sequence of consecutive observations. Assuming that the parameters are compressible, we analyze the performance of the $\ell_1$-regularized least squares as well as a greedy estimator of the parameters and characterize the sampling trade-offs required for stable recovery in the non-asymptotic regime. In particular, we show that for a fixed sparsity level, stable recovery of AR parameters is possible when the number of samples scale sub-linearly with the AR order. Our results improve over existing sampling complexity requirements in AR estimation using the LASSO, when the sparsity level scales faster than the square root of the model order. We further derive sufficient conditions on the sparsity level that guarantee the minimax optimality of the $\ell_1$-regularized least squares estimate. Applying these techniques to simulated data as well as real-world datasets from crude oil prices and traffic speed data confirm our predicted theoretical performance gains in terms of estimation accuracy and model selection.

Efficient Estimation of Compressible State-Space Models with Application to Calcium Signal Deconvolution

In this paper, we consider linear state-space models with compressible innovations and convergent transition matrices in order to model spatiotemporally sparse transient events. We perform parameter and state estimation using a dynamic compressed sensing framework and develop an efficient solution consisting of two nested Expectation-Maximization (EM) algorithms. Under suitable sparsity assumptions on the innovations, we prove recovery guarantees and derive confidence bounds for the state estimates. We provide simulation studies as well as application to spike deconvolution from calcium imaging data which verify our theoretical results and show significant improvement over existing algorithms.