Rethinking Fine-Tuning when Scaling Test-Time Compute: Limiting Confidence Improves Mathematical Reasoning

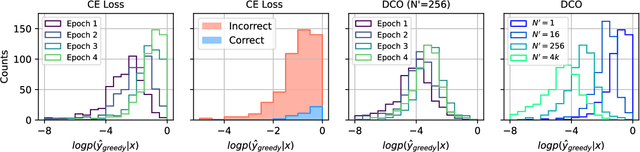
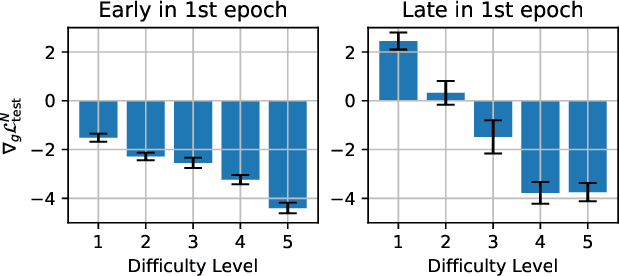
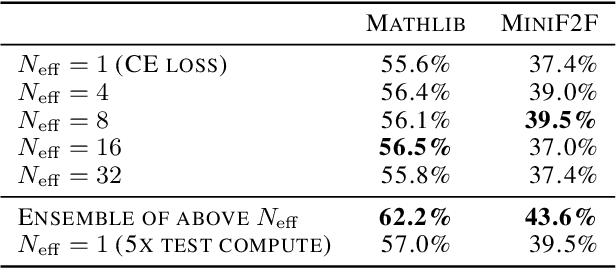
Recent progress in large language models (LLMs) highlights the power of scaling test-time compute to achieve strong performance on complex tasks, such as mathematical reasoning and code generation. This raises a critical question: how should model training be modified to optimize performance under a subsequent test-time compute strategy and budget? To explore this, we focus on pass@N, a simple test-time strategy that searches for a correct answer in $N$ independent samples. We show, surprisingly, that training with cross-entropy (CE) loss can be ${\it misaligned}$ with pass@N in that pass@N accuracy ${\it decreases}$ with longer training. We explain the origins of this misalignment in terms of model overconfidence induced by CE, and experimentally verify our prediction of overconfidence as an impediment to scaling test-time compute via pass@N. Furthermore we suggest a principled, modified training loss that is better aligned to pass@N by limiting model confidence and rescuing pass@N test performance. Our algorithm demonstrates improved mathematical reasoning on MATH and MiniF2F benchmarks under several scenarios: (1) providing answers to math questions; and (2) proving theorems by searching over proof trees of varying shapes. Overall our work underscores the importance of co-designing two traditionally separate phases of LLM development: training-time protocols and test-time search and reasoning strategies.

A Cross-Modal Approach to Silent Speech with LLM-Enhanced Recognition

Silent Speech Interfaces (SSIs) offer a noninvasive alternative to brain-computer interfaces for soundless verbal communication. We introduce Multimodal Orofacial Neural Audio (MONA), a system that leverages cross-modal alignment through novel loss functions--cross-contrast (crossCon) and supervised temporal contrast (supTcon)--to train a multimodal model with a shared latent representation. This architecture enables the use of audio-only datasets like LibriSpeech to improve silent speech recognition. Additionally, our introduction of Large Language Model (LLM) Integrated Scoring Adjustment (LISA) significantly improves recognition accuracy. Together, MONA LISA reduces the state-of-the-art word error rate (WER) from 28.8% to 12.2% in the Gaddy (2020) benchmark dataset for silent speech on an open vocabulary. For vocal EMG recordings, our method improves the state-of-the-art from 23.3% to 3.7% WER. In the Brain-to-Text 2024 competition, LISA performs best, improving the top WER from 9.8% to 8.9%. To the best of our knowledge, this work represents the first instance where noninvasive silent speech recognition on an open vocabulary has cleared the threshold of 15% WER, demonstrating that SSIs can be a viable alternative to automatic speech recognition (ASR). Our work not only narrows the performance gap between silent and vocalized speech but also opens new possibilities in human-computer interaction, demonstrating the potential of cross-modal approaches in noisy and data-limited regimes.

No Spurious Local Minima in Deep Quadratic Networks

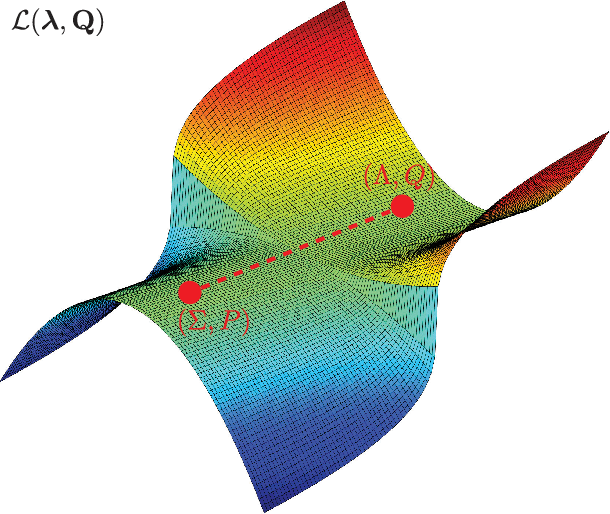
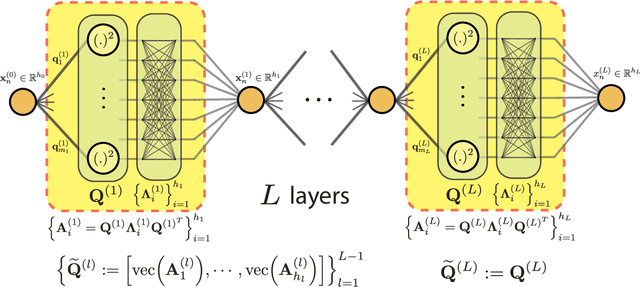
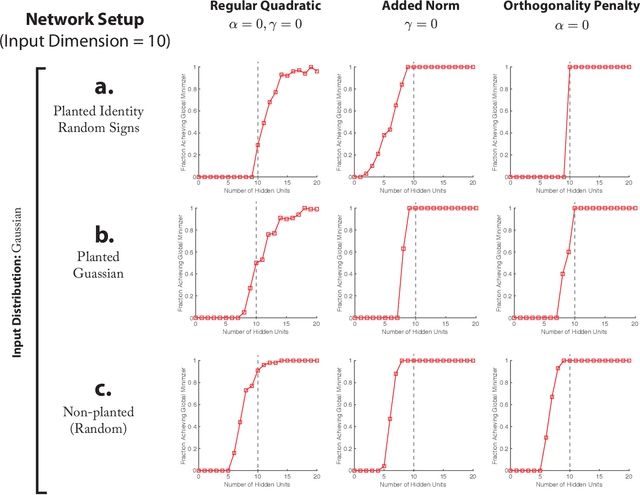
Despite their practical success, a theoretical understanding of the loss landscape of neural networks has proven challenging due to the high-dimensional, non-convex, and highly nonlinear structure of such models. In this paper, we characterize the training landscape of the quadratic loss landscape for neural networks with quadratic activation functions. We prove existence of spurious local minima and saddle points which can be escaped easily with probability one when the number of neurons is greater than or equal to the input dimension and the norm of the training samples is used as a regressor. We prove that deep overparameterized neural networks with quadratic activations benefit from similar nice landscape properties. Our theoretical results are independent of data distribution and fill the existing gap in theory for two-layer quadratic neural networks. Finally, we empirically demonstrate convergence to a global minimum for these problems.