Efficient Covering Using Reed--Solomon Codes

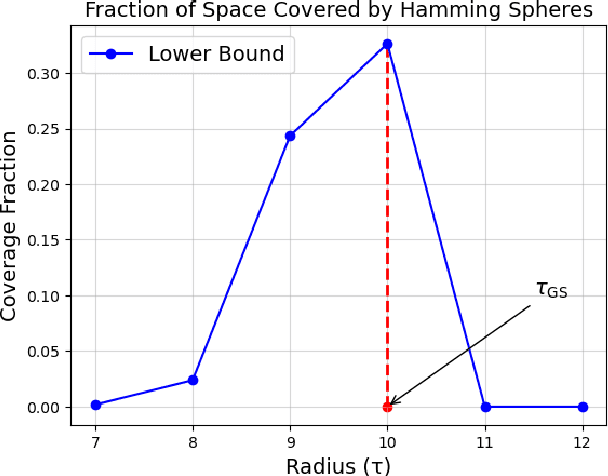
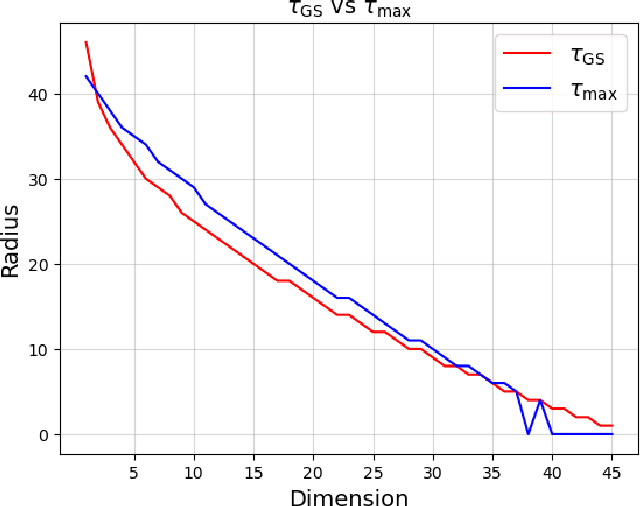
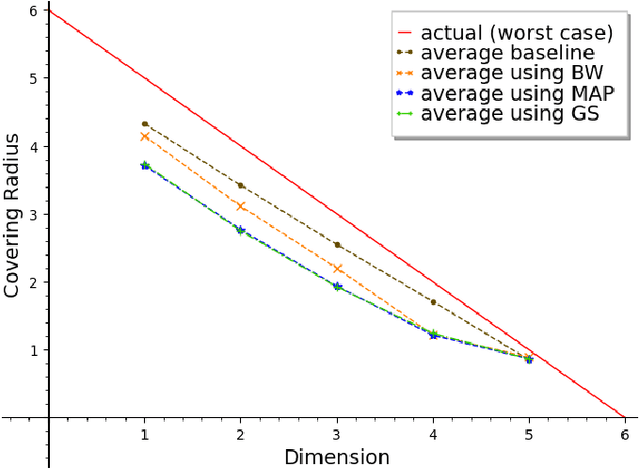
We propose an efficient algorithm to find a Reed-Solomon (RS) codeword at a distance within the covering radius of the code from any point in its ambient Hamming space. To the best of the authors' knowledge, this is the first attempt of its kind to solve the covering problem for RS codes. The proposed algorithm leverages off-the-shelf decoding methods for RS codes, including the Berlekamp-Welch algorithm for unique decoding and the Guruswami-Sudan algorithm for list decoding. We also present theoretical and numerical results on the capabilities of the proposed algorithm and, in particular, the average covering radius resulting from it. Our numerical results suggest that the overlapping Hamming spheres of radius close to the Guruswami-Sudan decoding radius centered at the codewords cover most of the ambient Hamming space.

Precoding Design for Limited-Feedback MISO Systems via Character-Polynomial Codes

We consider the problem of Multiple-Input Single- Output (MISO) communication with limited feedback, where the transmitter relies on a limited number of bits associated with the channel state information (CSI), available at the receiver (CSIR) but not at the transmitter (no CSIT), sent via the feedback link. We demonstrate how character-polynomial (CP) codes, a class of analog subspace codes (also, referred to as Grassmann codes) can be used for the corresponding quantization problem in the Grassmann space. The proposed CP codebook-based precoding design allows for a smooth trade-off between the number of feedback bits and the beamforming gain, by simply adjusting the rate of the underlying CP code. We present a theoretical upper bound on the mean squared quantization error of the CP codebook, and utilize it to upper bound the resulting distortion as the normalized gap between the CP codebook beamforming gain and the baseline equal gain transmission (EGT) with perfect CSIT. We further show that the distortion vanishes asymptotically. The results are also confirmed via simulations for different types of fading models in the MISO system and various parameters.

Decoding Analog Subspace Codes: Algorithms for Character-Polynomial Codes

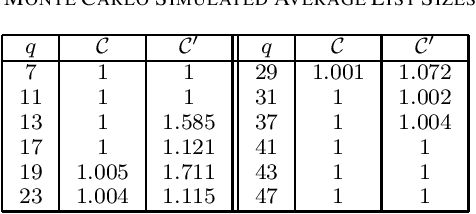
We propose efficient minimum-distance decoding and list-decoding algorithms for a certain class of analog subspace codes, referred to as character-polynomial (CP) codes, recently introduced by Soleymani and the second author. In particular, a CP code without its character can be viewed as a subcode of a Reed--Solomon (RS) code, where a certain subset of the coefficients of the message polynomial is set to zeros. We then demonstrate how classical decoding methods, including list decoders, for RS codes can be leveraged for decoding CP codes. For instance, it is shown that, in almost all cases, the list decoder behaves as a unique decoder. We also present a probabilistic analysis of the improvements in list decoding of CP codes when leveraging their certain structure as subcodes of RS codes.