Efficient Covering Using Reed--Solomon Codes
Paper and Code
Feb 04, 2025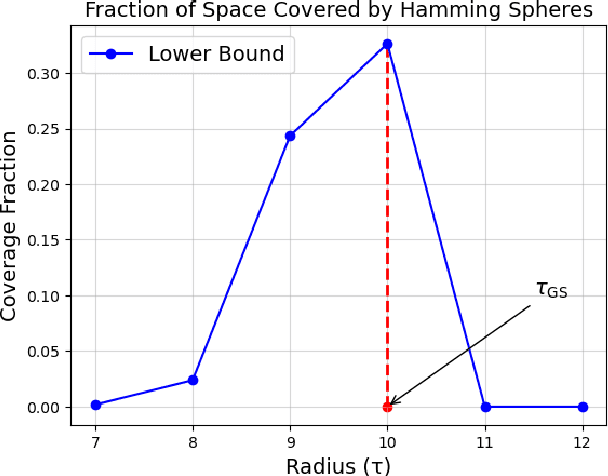
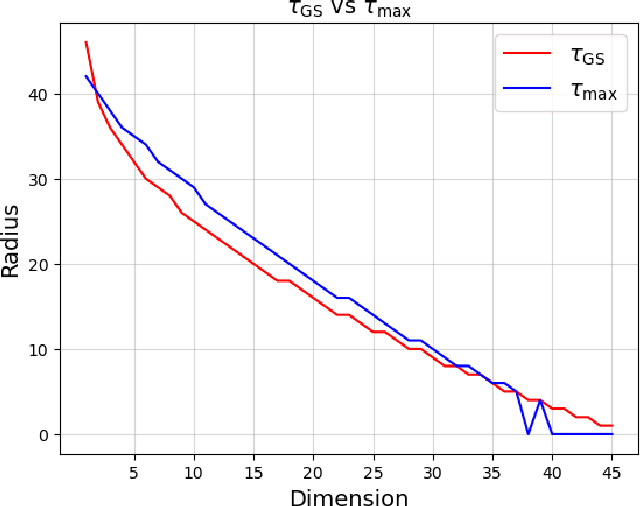
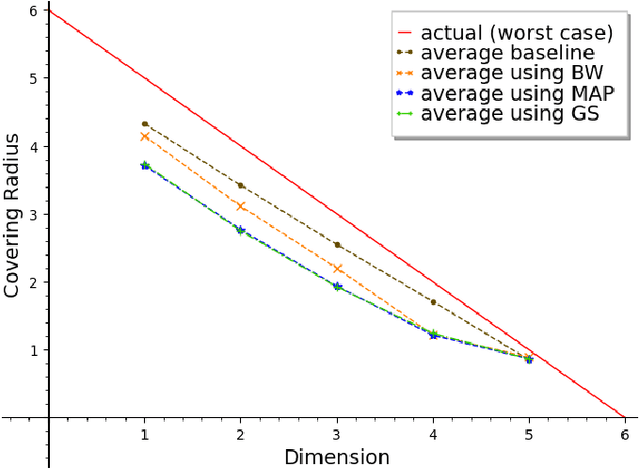

We propose an efficient algorithm to find a Reed-Solomon (RS) codeword at a distance within the covering radius of the code from any point in its ambient Hamming space. To the best of the authors' knowledge, this is the first attempt of its kind to solve the covering problem for RS codes. The proposed algorithm leverages off-the-shelf decoding methods for RS codes, including the Berlekamp-Welch algorithm for unique decoding and the Guruswami-Sudan algorithm for list decoding. We also present theoretical and numerical results on the capabilities of the proposed algorithm and, in particular, the average covering radius resulting from it. Our numerical results suggest that the overlapping Hamming spheres of radius close to the Guruswami-Sudan decoding radius centered at the codewords cover most of the ambient Hamming space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge