Transformers on Markov Data: Constant Depth Suffices

Attention-based transformers have been remarkably successful at modeling generative processes across various domains and modalities. In this paper, we study the behavior of transformers on data drawn from \kth Markov processes, where the conditional distribution of the next symbol in a sequence depends on the previous $k$ symbols observed. We observe a surprising phenomenon empirically which contradicts previous findings: when trained for sufficiently long, a transformer with a fixed depth and $1$ head per layer is able to achieve low test loss on sequences drawn from \kth Markov sources, even as $k$ grows. Furthermore, this low test loss is achieved by the transformer's ability to represent and learn the in-context conditional empirical distribution. On the theoretical side, our main result is that a transformer with a single head and three layers can represent the in-context conditional empirical distribution for \kth Markov sources, concurring with our empirical observations. Along the way, we prove that \textit{attention-only} transformers with $O(\log_2(k))$ layers can represent the in-context conditional empirical distribution by composing induction heads to track the previous $k$ symbols in the sequence. These results provide more insight into our current understanding of the mechanisms by which transformers learn to capture context, by understanding their behavior on Markov sources.

Fundamental Limits of Prompt Compression: A Rate-Distortion Framework for Black-Box Language Models

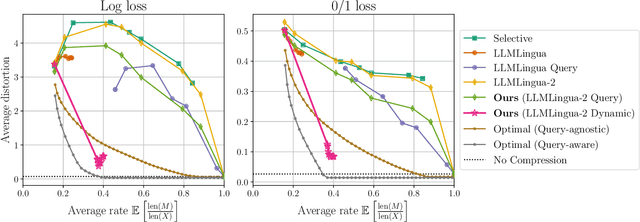
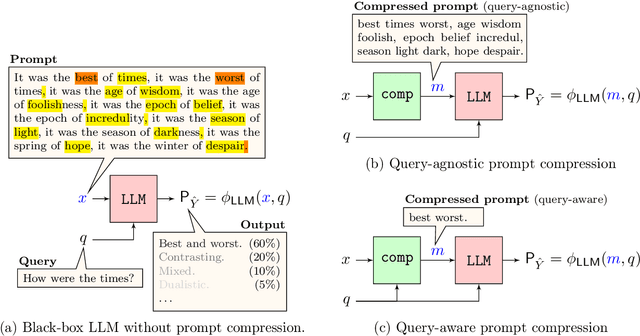
We formalize the problem of prompt compression for large language models (LLMs) and present a framework to unify token-level prompt compression methods which create hard prompts for black-box models. We derive the distortion-rate function for this setup as a linear program, and provide an efficient algorithm to compute this fundamental limit via the dual of the linear program. Using the distortion-rate function as the baseline, we study the performance of existing compression schemes on a synthetic dataset consisting of prompts generated from a Markov chain, natural language queries, and their respective answers. Our empirical analysis demonstrates the criticality of query-aware prompt compression, where the compressor has knowledge of the downstream task/query for the black-box LLM. We show that there is a large gap between the performance of current prompt compression methods and the optimal strategy, and propose a query-aware, variable-rate adaptation of a prior work to close the gap. We extend our experiments to a small natural language dataset to further confirm our findings on our synthetic dataset.

Local to Global: Learning Dynamics and Effect of Initialization for Transformers

In recent years, transformer-based models have revolutionized deep learning, particularly in sequence modeling. To better understand this phenomenon, there is a growing interest in using Markov input processes to study transformers. However, our current understanding in this regard remains limited with many fundamental questions about how transformers learn Markov chains still unanswered. In this paper, we address this by focusing on first-order Markov chains and single-layer transformers, providing a comprehensive characterization of the learning dynamics in this context. Specifically, we prove that transformer parameters trained on next-token prediction loss can either converge to global or local minima, contingent on the initialization and the Markovian data properties, and we characterize the precise conditions under which this occurs. To the best of our knowledge, this is the first result of its kind highlighting the role of initialization. We further demonstrate that our theoretical findings are corroborated by empirical evidence. Based on these insights, we provide guidelines for the initialization of transformer parameters and demonstrate their effectiveness. Finally, we outline several open problems in this arena. Code is available at: \url{https://anonymous.4open.science/r/Local-to-Global-C70B/}.

Attention with Markov: A Framework for Principled Analysis of Transformers via Markov Chains

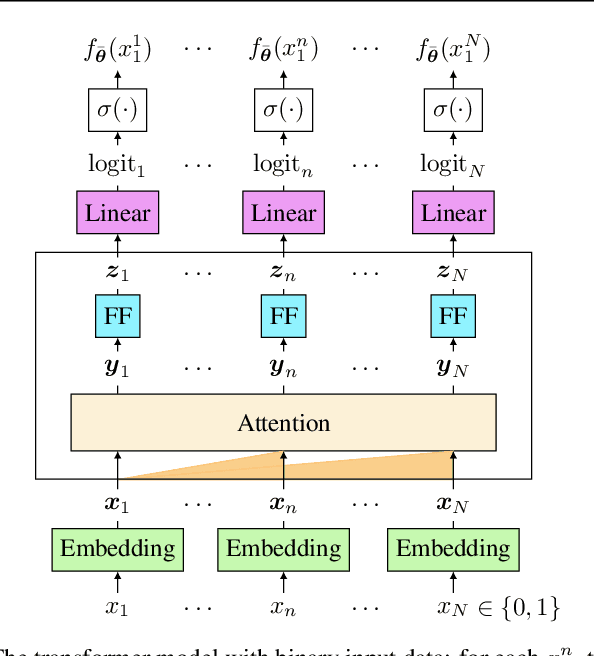
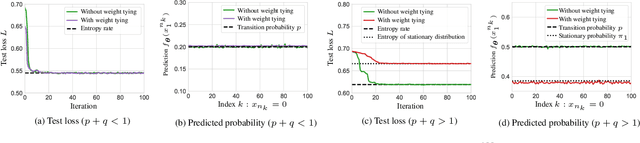
In recent years, attention-based transformers have achieved tremendous success across a variety of disciplines including natural languages. A key ingredient behind their success is the generative pretraining procedure, during which these models are trained on a large text corpus in an auto-regressive manner. To shed light on this phenomenon, we propose a new framework that allows both theory and systematic experiments to study the sequential modeling capabilities of transformers through the lens of Markov chains. Inspired by the Markovianity of natural languages, we model the data as a Markovian source and utilize this framework to systematically study the interplay between the data-distributional properties, the transformer architecture, the learnt distribution, and the final model performance. In particular, we theoretically characterize the loss landscape of single-layer transformers and show the existence of global minima and bad local minima contingent upon the specific data characteristics and the transformer architecture. Backed by experiments, we demonstrate that our theoretical findings are in congruence with the empirical results. We further investigate these findings in the broader context of higher order Markov chains and deeper architectures, and outline open problems in this arena. Code is available at \url{https://github.com/Bond1995/Markov}.

LASER: Linear Compression in Wireless Distributed Optimization

Data-parallel SGD is the de facto algorithm for distributed optimization, especially for large scale machine learning. Despite its merits, communication bottleneck is one of its persistent issues. Most compression schemes to alleviate this either assume noiseless communication links, or fail to achieve good performance on practical tasks. In this paper, we close this gap and introduce LASER: LineAr CompreSsion in WirEless DistRibuted Optimization. LASER capitalizes on the inherent low-rank structure of gradients and transmits them efficiently over the noisy channels. Whilst enjoying theoretical guarantees similar to those of the classical SGD, LASER shows consistent gains over baselines on a variety of practical benchmarks. In particular, it outperforms the state-of-the-art compression schemes on challenging computer vision and GPT language modeling tasks. On the latter, we obtain $50$-$64 \%$ improvement in perplexity over our baselines for noisy channels.

Machine Learning-Aided Efficient Decoding of Reed-Muller Subcodes

Reed-Muller (RM) codes achieve the capacity of general binary-input memoryless symmetric channels and have a comparable performance to that of random codes in terms of scaling laws. However, they lack efficient decoders with performance close to that of a maximum-likelihood decoder for general code parameters. Also, they only admit limited sets of rates. In this paper, we focus on subcodes of RM codes with flexible rates. We first extend the recently-introduced recursive projection-aggregation (RPA) decoding algorithm to RM subcodes. To lower the complexity of our decoding algorithm, referred to as subRPA, we investigate different approaches to prune the projections. Next, we derive the soft-decision based version of our algorithm, called soft-subRPA, that not only improves upon the performance of subRPA but also enables a differentiable decoding algorithm. Building upon the soft-subRPA algorithm, we then provide a framework for training a machine learning (ML) model to search for \textit{good} sets of projections that minimize the decoding error rate. Training our ML model enables achieving very close to the performance of full-projection decoding with a significantly smaller number of projections. We also show that the choice of the projections in decoding RM subcodes matters significantly, and our ML-aided projection pruning scheme is able to find a \textit{good} selection, i.e., with negligible performance degradation compared to the full-projection case, given a reasonable number of projections.

CRISP: Curriculum based Sequential Neural Decoders for Polar Code Family

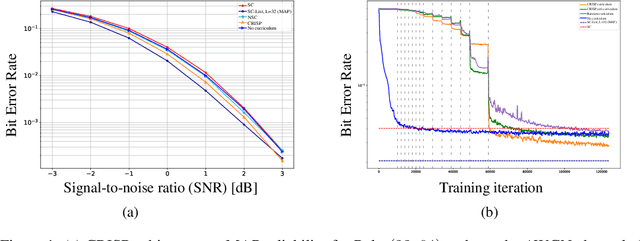
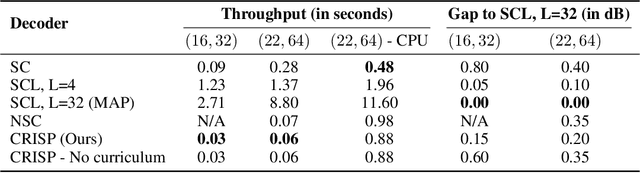
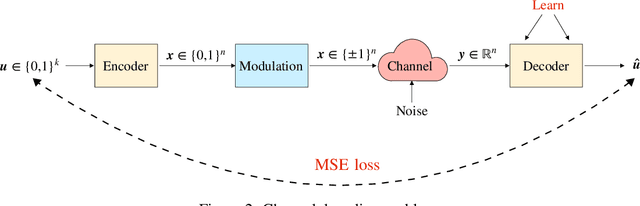
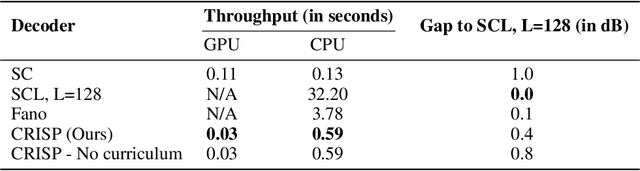
Polar codes are widely used state-of-the-art codes for reliable communication that have recently been included in the 5th generation wireless standards (5G). However, there remains room for the design of polar decoders that are both efficient and reliable in the short blocklength regime. Motivated by recent successes of data-driven channel decoders, we introduce a novel $\textbf{C}$ur$\textbf{RI}$culum based $\textbf{S}$equential neural decoder for $\textbf{P}$olar codes (CRISP). We design a principled curriculum, guided by information-theoretic insights, to train CRISP and show that it outperforms the successive-cancellation (SC) decoder and attains near-optimal reliability performance on the Polar(16,32) and Polar(22, 64) codes. The choice of the proposed curriculum is critical in achieving the accuracy gains of CRISP, as we show by comparing against other curricula. More notably, CRISP can be readily extended to Polarization-Adjusted-Convolutional (PAC) codes, where existing SC decoders are significantly less reliable. To the best of our knowledge, CRISP constructs the first data-driven decoder for PAC codes and attains near-optimal performance on the PAC(16, 32) code.

KO codes: Inventing Nonlinear Encoding and Decoding for Reliable Wireless Communication via Deep-learning

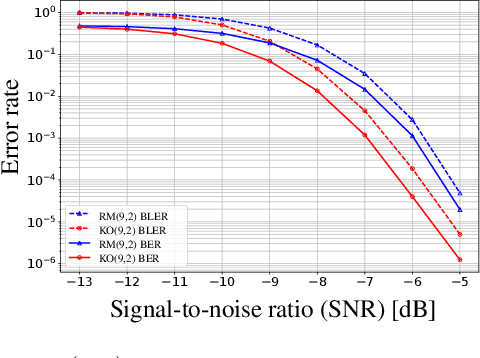
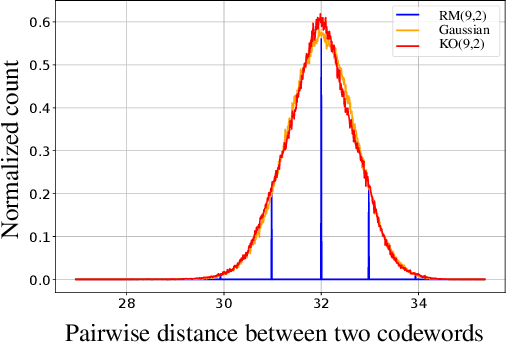
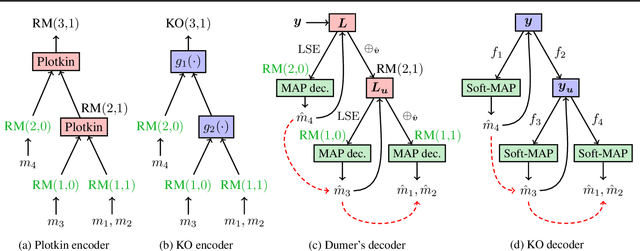
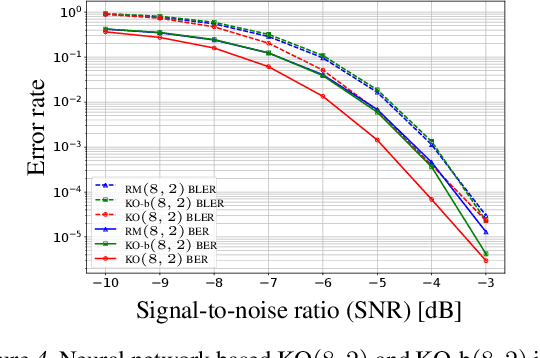
Landmark codes underpin reliable physical layer communication, e.g., Reed-Muller, BCH, Convolution, Turbo, LDPC and Polar codes: each is a linear code and represents a mathematical breakthrough. The impact on humanity is huge: each of these codes has been used in global wireless communication standards (satellite, WiFi, cellular). Reliability of communication over the classical additive white Gaussian noise (AWGN) channel enables benchmarking and ranking of the different codes. In this paper, we construct KO codes, a computationaly efficient family of deep-learning driven (encoder, decoder) pairs that outperform the state-of-the-art reliability performance on the standardized AWGN channel. KO codes beat state-of-the-art Reed-Muller and Polar codes, under the low-complexity successive cancellation decoding, in the challenging short-to-medium block length regime on the AWGN channel. We show that the gains of KO codes are primarily due to the nonlinear mapping of information bits directly to transmit real symbols (bypassing modulation) and yet possess an efficient, high performance decoder. The key technical innovation that renders this possible is design of a novel family of neural architectures inspired by the computation tree of the {\bf K}ronecker {\bf O}peration (KO) central to Reed-Muller and Polar codes. These architectures pave way for the discovery of a much richer class of hitherto unexplored nonlinear algebraic structures. The code is available at \href{https://github.com/deepcomm/KOcodes}{https://github.com/deepcomm/KOcodes}

Optimal transport mapping via input convex neural networks

In this paper, we present a novel and principled approach to learn the optimal transport between two distributions, from samples. Guided by the optimal transport theory, we learn the optimal Kantorovich potential which induces the optimal transport map. This involves learning two convex functions, by solving a novel minimax optimization. Building upon recent advances in the field of input convex neural networks, we propose a new framework where the gradient of one convex function represents the optimal transport mapping. Numerical experiments confirm that we learn the optimal transport mapping. This approach ensures that the transport mapping we find is optimal independent of how we initialize the neural networks. Further, target distributions from a discontinuous support can be easily captured, as gradient of a convex function naturally models a {\em discontinuous} transport mapping.

Learning in Gated Neural Networks

Gating is a key feature in modern neural networks including LSTMs, GRUs and sparsely-gated deep neural networks. The backbone of such gated networks is a mixture-of-experts layer, where several experts make regression decisions and gating controls how to weigh the decisions in an input-dependent manner. Despite having such a prominent role in both modern and classical machine learning, very little is understood about parameter recovery of mixture-of-experts since gradient descent and EM algorithms are known to be stuck in local optima in such models. In this paper, we perform a careful analysis of the optimization landscape and show that with appropriately designed loss functions, gradient descent can indeed learn the parameters accurately. A key idea underpinning our results is the design of two {\em distinct} loss functions, one for recovering the expert parameters and another for recovering the gating parameters. We demonstrate the first sample complexity results for parameter recovery in this model for any algorithm and demonstrate significant performance gains over standard loss functions in numerical experiments.