Accurate and scalable exchange-correlation with deep learning

Density Functional Theory (DFT) is the most widely used electronic structure method for predicting the properties of molecules and materials. Although DFT is, in principle, an exact reformulation of the Schr\"odinger equation, practical applications rely on approximations to the unknown exchange-correlation (XC) functional. Most existing XC functionals are constructed using a limited set of increasingly complex, hand-crafted features that improve accuracy at the expense of computational efficiency. Yet, no current approximation achieves the accuracy and generality for predictive modeling of laboratory experiments at chemical accuracy -- typically defined as errors below 1 kcal/mol. In this work, we present Skala, a modern deep learning-based XC functional that bypasses expensive hand-designed features by learning representations directly from data. Skala achieves chemical accuracy for atomization energies of small molecules while retaining the computational efficiency typical of semi-local DFT. This performance is enabled by training on an unprecedented volume of high-accuracy reference data generated using computationally intensive wavefunction-based methods. Notably, Skala systematically improves with additional training data covering diverse chemistry. By incorporating a modest amount of additional high-accuracy data tailored to chemistry beyond atomization energies, Skala achieves accuracy competitive with the best-performing hybrid functionals across general main group chemistry, at the cost of semi-local DFT. As the training dataset continues to expand, Skala is poised to further enhance the predictive power of first-principles simulations.

Exponential Moving Average of Weights in Deep Learning: Dynamics and Benefits

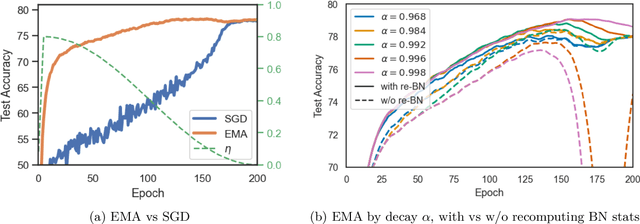
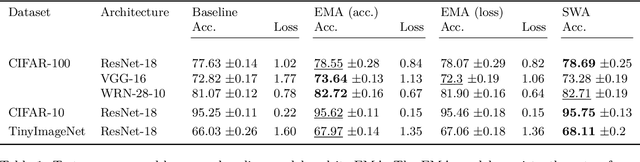
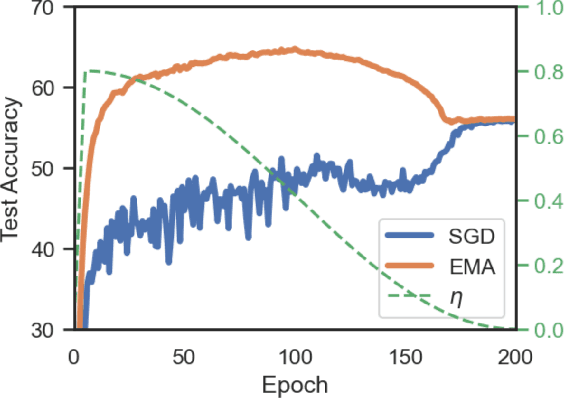
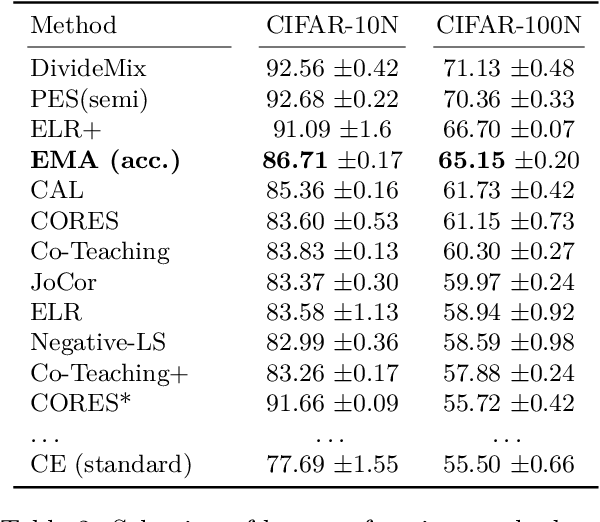
Weight averaging of Stochastic Gradient Descent (SGD) iterates is a popular method for training deep learning models. While it is often used as part of complex training pipelines to improve generalization or serve as a `teacher' model, weight averaging lacks proper evaluation on its own. In this work, we present a systematic study of the Exponential Moving Average (EMA) of weights. We first explore the training dynamics of EMA, give guidelines for hyperparameter tuning, and highlight its good early performance, partly explaining its success as a teacher. We also observe that EMA requires less learning rate decay compared to SGD since averaging naturally reduces noise, introducing a form of implicit regularization. Through extensive experiments, we show that EMA solutions differ from last-iterate solutions. EMA models not only generalize better but also exhibit improved i) robustness to noisy labels, ii) prediction consistency, iii) calibration and iv) transfer learning. Therefore, we suggest that an EMA of weights is a simple yet effective plug-in to improve the performance of deep learning models.

LASER: Linear Compression in Wireless Distributed Optimization

Data-parallel SGD is the de facto algorithm for distributed optimization, especially for large scale machine learning. Despite its merits, communication bottleneck is one of its persistent issues. Most compression schemes to alleviate this either assume noiseless communication links, or fail to achieve good performance on practical tasks. In this paper, we close this gap and introduce LASER: LineAr CompreSsion in WirEless DistRibuted Optimization. LASER capitalizes on the inherent low-rank structure of gradients and transmits them efficiently over the noisy channels. Whilst enjoying theoretical guarantees similar to those of the classical SGD, LASER shows consistent gains over baselines on a variety of practical benchmarks. In particular, it outperforms the state-of-the-art compression schemes on challenging computer vision and GPT language modeling tasks. On the latter, we obtain $50$-$64 \%$ improvement in perplexity over our baselines for noisy channels.

MultiModN- Multimodal, Multi-Task, Interpretable Modular Networks

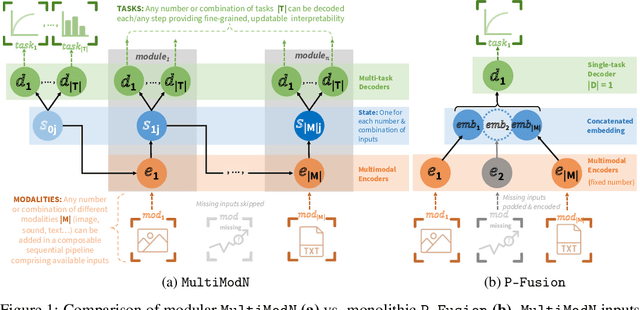
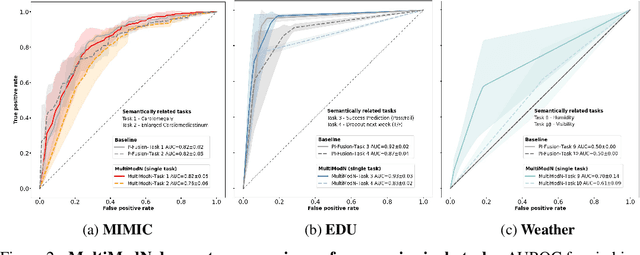
Predicting multiple real-world tasks in a single model often requires a particularly diverse feature space. Multimodal (MM) models aim to extract the synergistic predictive potential of multiple data types to create a shared feature space with aligned semantic meaning across inputs of drastically varying sizes (i.e. images, text, sound). Most current MM architectures fuse these representations in parallel, which not only limits their interpretability but also creates a dependency on modality availability. We present MultiModN, a multimodal, modular network that fuses latent representations in a sequence of any number, combination, or type of modality while providing granular real-time predictive feedback on any number or combination of predictive tasks. MultiModN's composable pipeline is interpretable-by-design, as well as innately multi-task and robust to the fundamental issue of biased missingness. We perform four experiments on several benchmark MM datasets across 10 real-world tasks (predicting medical diagnoses, academic performance, and weather), and show that MultiModN's sequential MM fusion does not compromise performance compared with a baseline of parallel fusion. By simulating the challenging bias of missing not-at-random (MNAR), this work shows that, contrary to MultiModN, parallel fusion baselines erroneously learn MNAR and suffer catastrophic failure when faced with different patterns of MNAR at inference. To the best of our knowledge, this is the first inherently MNAR-resistant approach to MM modeling. In conclusion, MultiModN provides granular insights, robustness, and flexibility without compromising performance.

Beyond spectral gap : The role of the topology in decentralized learning

In data-parallel optimization of machine learning models, workers collaborate to improve their estimates of the model: more accurate gradients allow them to use larger learning rates and optimize faster. In the decentralized setting, in which workers communicate over a sparse graph, current theory fails to capture important aspects of real-world behavior. First, the `spectral gap' of the communication graph is not predictive of its empirical performance in (deep) learning. Second, current theory does not explain that collaboration enables larger learning rates than training alone. In fact, it prescribes smaller learning rates, which further decrease as graphs become larger, failing to explain convergence dynamics in infinite graphs. This paper aims to paint an accurate picture of sparsely-connected distributed optimization. We quantify how the graph topology influences convergence in a quadratic toy problem and provide theoretical results for general smooth and (strongly) convex objectives. Our theory matches empirical observations in deep learning, and accurately describes the relative merits of different graph topologies. This paper is an extension of the conference paper by Vogels et. al. (2022). Code: https://github.com/epfml/topology-in-decentralized-learning.

Modular Clinical Decision Support Networks (MoDN) -- Updatable, Interpretable, and Portable Predictions for Evolving Clinical Environments

Data-driven Clinical Decision Support Systems (CDSS) have the potential to improve and standardise care with personalised probabilistic guidance. However, the size of data required necessitates collaborative learning from analogous CDSS's, which are often unsharable or imperfectly interoperable (IIO), meaning their feature sets are not perfectly overlapping. We propose Modular Clinical Decision Support Networks (MoDN) which allow flexible, privacy-preserving learning across IIO datasets, while providing interpretable, continuous predictive feedback to the clinician. MoDN is a novel decision tree composed of feature-specific neural network modules. It creates dynamic personalised representations of patients, and can make multiple predictions of diagnoses, updatable at each step of a consultation. The modular design allows it to compartmentalise training updates to specific features and collaboratively learn between IIO datasets without sharing any data.

Beyond spectral gap: The role of the topology in decentralized learning

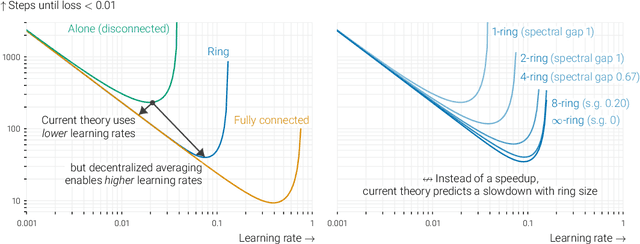
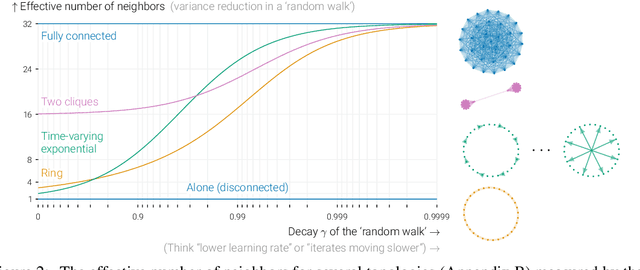
In data-parallel optimization of machine learning models, workers collaborate to improve their estimates of the model: more accurate gradients allow them to use larger learning rates and optimize faster. We consider the setting in which all workers sample from the same dataset, and communicate over a sparse graph (decentralized). In this setting, current theory fails to capture important aspects of real-world behavior. First, the 'spectral gap' of the communication graph is not predictive of its empirical performance in (deep) learning. Second, current theory does not explain that collaboration enables larger learning rates than training alone. In fact, it prescribes smaller learning rates, which further decrease as graphs become larger, failing to explain convergence in infinite graphs. This paper aims to paint an accurate picture of sparsely-connected distributed optimization when workers share the same data distribution. We quantify how the graph topology influences convergence in a quadratic toy problem and provide theoretical results for general smooth and (strongly) convex objectives. Our theory matches empirical observations in deep learning, and accurately describes the relative merits of different graph topologies.

RelaySum for Decentralized Deep Learning on Heterogeneous Data

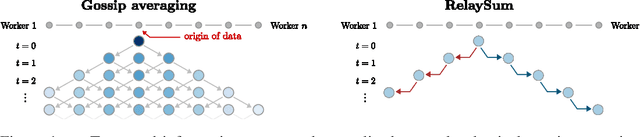
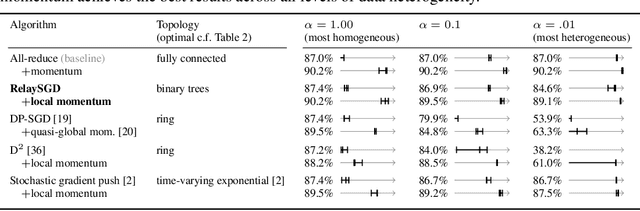
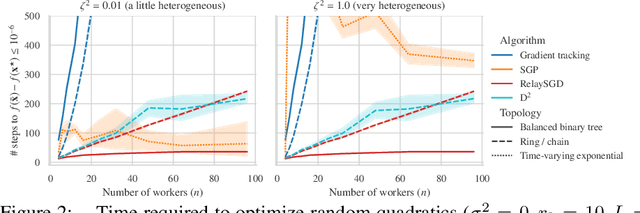
In decentralized machine learning, workers compute model updates on their local data. Because the workers only communicate with few neighbors without central coordination, these updates propagate progressively over the network. This paradigm enables distributed training on networks without all-to-all connectivity, helping to protect data privacy as well as to reduce the communication cost of distributed training in data centers. A key challenge, primarily in decentralized deep learning, remains the handling of differences between the workers' local data distributions. To tackle this challenge, we introduce the RelaySum mechanism for information propagation in decentralized learning. RelaySum uses spanning trees to distribute information exactly uniformly across all workers with finite delays depending on the distance between nodes. In contrast, the typical gossip averaging mechanism only distributes data uniformly asymptotically while using the same communication volume per step as RelaySum. We prove that RelaySGD, based on this mechanism, is independent of data heterogeneity and scales to many workers, enabling highly accurate decentralized deep learning on heterogeneous data. Our code is available at http://github.com/epfml/relaysgd.

PowerGossip: Practical Low-Rank Communication Compression in Decentralized Deep Learning

Lossy gradient compression has become a practical tool to overcome the communication bottleneck in centrally coordinated distributed training of machine learning models. However, algorithms for decentralized training with compressed communication over arbitrary connected networks have been more complicated, requiring additional memory and hyperparameters. We introduce a simple algorithm that directly compresses the model differences between neighboring workers using low-rank linear compressors applied on model differences. Inspired by the PowerSGD algorithm for centralized deep learning, this algorithm uses power iteration steps to maximize the information transferred per bit. We prove that our method requires no additional hyperparameters, converges faster than prior methods, and is asymptotically independent of both the network and the compression. Out of the box, these compressors perform on par with state-of-the-art tuned compression algorithms in a series of deep learning benchmarks.

On the Tunability of Optimizers in Deep Learning

There is no consensus yet on the question whether adaptive gradient methods like Adam are easier to use than non-adaptive optimization methods like SGD. In this work, we fill in the important, yet ambiguous concept of `ease-of-use' by defining an optimizer's \emph{tunability}: How easy is it to find good hyperparameter configurations using automatic random hyperparameter search? We propose a practical and universal quantitative measure for optimizer tunability that can form the basis for a fair optimizer benchmark. Evaluating a variety of optimizers on an extensive set of standard datasets and architectures, we find that Adam is the most tunable for the majority of problems, especially with a low budget for hyperparameter tuning.